MSBSHSE Solutions For Class 8 Maths Part 2 Chapter 11 Statistics are given here to help students with their exam preparations. As students are familiar with numbers and then comes the data interpretation and analysis, which are studied under statistics. This chapter discusses arithmetic mean, creation of sub-divided bar graphs and percentage bar graphs. All problems pertaining to these concepts are in the Maharashtra State Board Class 8 Textbooks Part 2. Our expert faculty team have created solutions to these problems in a step-by-step manner, in order to help students understand the concepts clearly. Using these solutions one can attain a strong command over the subject. For students wishing to secure an excellent score, MSBSHSE Solutions Class 8 is a must. Students can access the solutions PDF of this chapter the Maharashtra Board Solutions for Class 8 Maths Chapter 11 Statistics, from the link provided below.
Download the PDF of Maharashtra Board Solutions For Class 8 Maths Part 2 Chapter 11 Statistics
Access answers to Maharashtra Board Solutions For Class 8 Maths Part 2 Chapter 11 Statistics.
Practice Set 11.1 Page No: 69
1. The following table shows the number of saplings planted by 30 students. Fill in the boxes and find the average number of saplings planted by each student.

Solution:
| No. of saplings (Scores) xi | No. of students (Frequency) fi | fi × xi |
| 1 | 4 | 4 |
| 2 | 6 | 12 |
| 3 | 12 | 36 |
| 4 | 8 | 32 |
| N = 30 | Ʃ fixi = 84 |
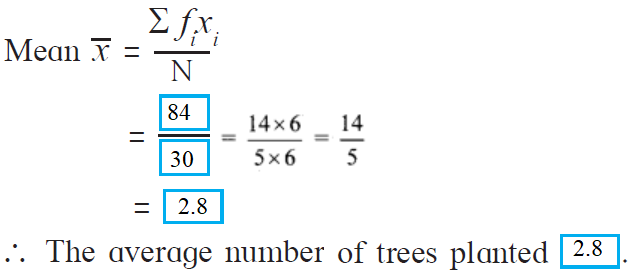
2. The following table shows the electricity (in units) used by 25 families of Eklara village in a month of May. Complete the table and answer the following questions.
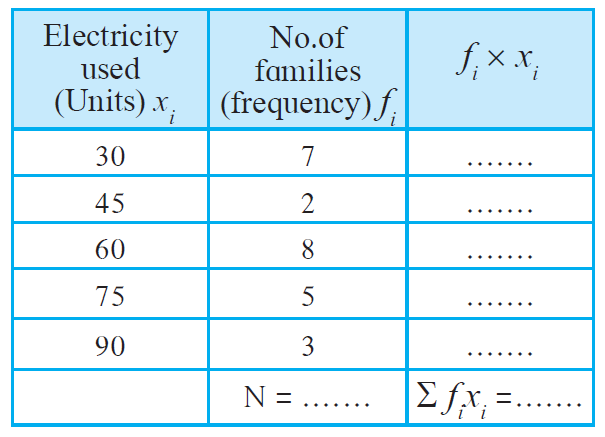
(1) How many families use 45 units electricity?
(2) State the score, the frequency of which is 5.
(3) Find N, and Ʃ fixi
(4) Find the mean of electricity used by each family in the month of May.
Solution:
| Electricity used (Units) xi | No. of families (Frequency) fi | fi × xi |
| 30 | 7 | 210 |
| 45 | 2 | 90 |
| 60 | 8 | 480 |
| 75 | 5 | 375 |
| 90 | 3 | 270 |
| N = 25 | Ʃ fixi = 1425 |
(1) 2 families used 45 units od electricity.
(2) The score for which the frequency is 5 is 75.
(3) N = 25 and Ʃ fixi = 1425
(4) The mean of electricity used by each family in the month of May is given by:
Mean () = Ʃ fixi / N
= 1425 / 25
= 57
Thus, the mean of electricity used by each family in the month of May is 57 units.
3. The number of members in the 40 families in Bhilar are as follows:
1, 6, 5, 4, 3, 2, 7, 2, 3, 4, 5, 6, 4, 6, 2, 3, 2, 1, 4, 5, 6, 7, 3, 4, 5, 2, 4, 3, 2, 3, 5, 5, 4, 6, 2, 3, 5, 6, 4, 2. Prepare a frequency table and find the mean of members of 40 families.
Solution:
| Number of members | Number of families (fi) | fixi |
| 1 | 2 | 2 |
| 2 | 8 | 16 |
| 3 | 7 | 21 |
| 4 | 8 | 32 |
| 5 | 7 | 35 |
| 6 | 6 | 36 |
| 7 | 2 | 14 |
| N = 40 | Ʃ fixi = 156 |
Now,
Mean = Ʃ fixi/ N = 156/ 40 = 3.9
Thus, the mean of members of 40 families is 3.9.
4. The number of Science and Mathematics projects submitted by Model high school, Nandpur in last 20 years at the state level science exhibition is : 2, 3, 4, 1, 2, 3, 1, 5, 4, 2, 3, 1, 3, 5, 4, 3, 2, 2, 3, 2. Prepare a frequency table and find the mean of the data.
Solution:
| Number of projects (xi) | Frequency (fi) | fixi |
| 1 | 3 | 3 |
| 2 | 6 | 12 |
| 3 | 6 | 18 |
| 4 | 3 | 12 |
| 5 | 2 | 10 |
| N = 20 | Ʃ fixi = 55 |
Now,
Mean = Ʃ fixi / N = 55/ 20 = 2.75
Thus, the mean of the data = 2.75
Practice Set 11.2 Page No: 71
1.
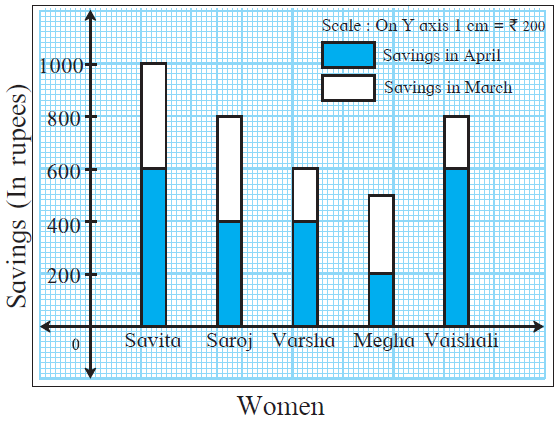
(1) State the type of the graph.
(2) How much is the savings of Vaishali in the month of April?
(3) How much is the total of savings of Saroj in the months March and April?
(4) How much more is the total savings of Savita than the total savings of Megha?
(5) Whose savings in the month of April is the least?
Solution:
(1) The given is a bar graph.
(2) The savings of Vaishali in the month of April is Rs 600.
(3) The total savings of Saroj in the months March and April is Rs 800.
(4) From the table it’s seen that, the total savings of Savita = Rs 1000
And, the total savings of Megha = Rs 500
So, the difference in their savings = 1000 − 500 = 500
Hence, the total savings of Savita is Rs 500 more than the total savings of Megha.
(5) The savings of Megha in the month of April is the least i.e. Rs 200.
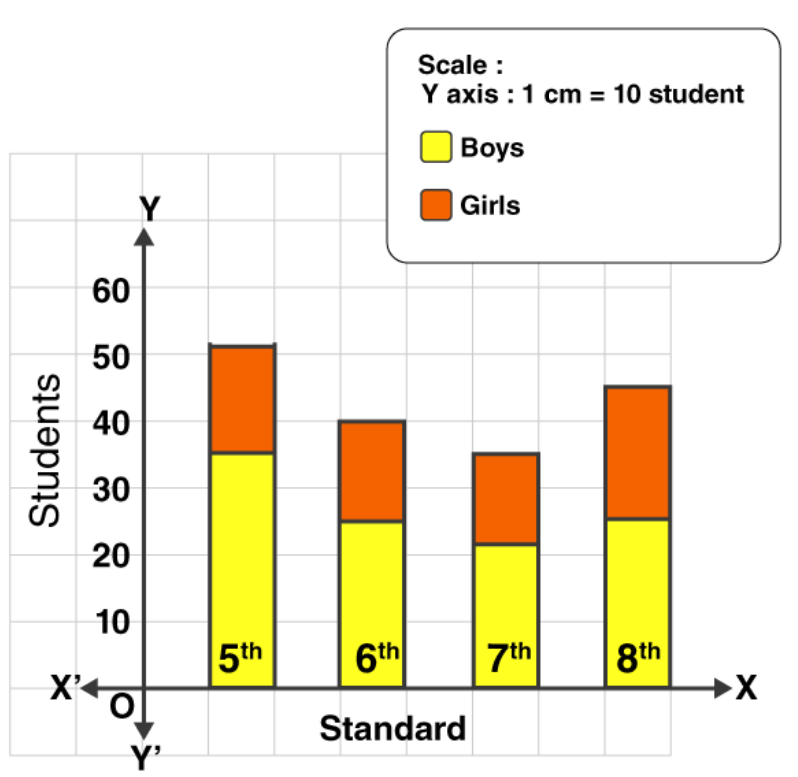
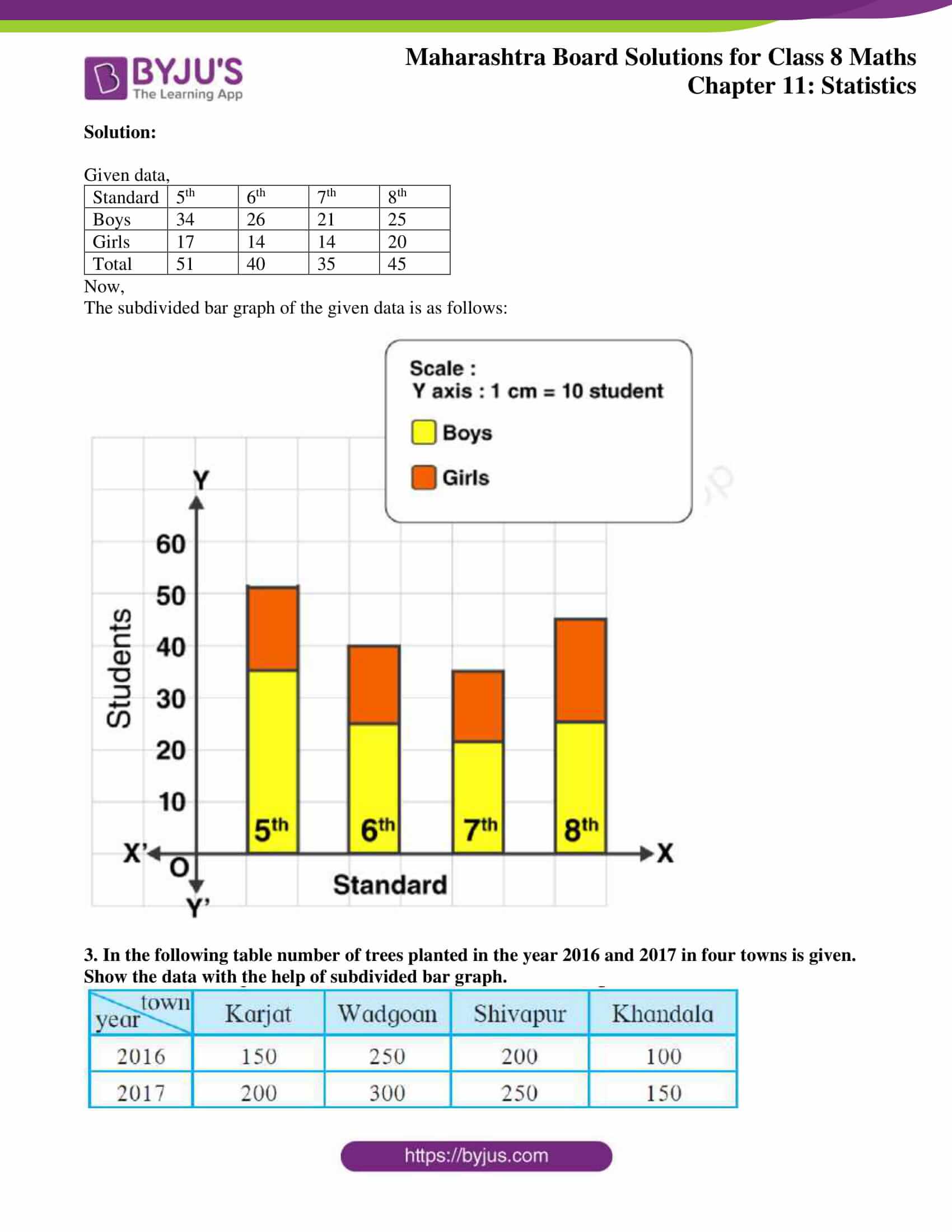
2. The number of boys and girls, in std 5 to std 8 in a Z.P. school is given in the table. Draw a subdivided bar graph to show the data.
(Scale: On Y axis, 1cm = 10 students)

Solution:
Given data,
| Standard | 5th | 6th | 7th | 8th |
| Boys | 34 | 26 | 21 | 25 |
| Girls | 17 | 14 | 14 | 20 |
| Total | 51 | 40 | 35 | 45 |
Now,
The subdivided bar graph of the given data is as follows:
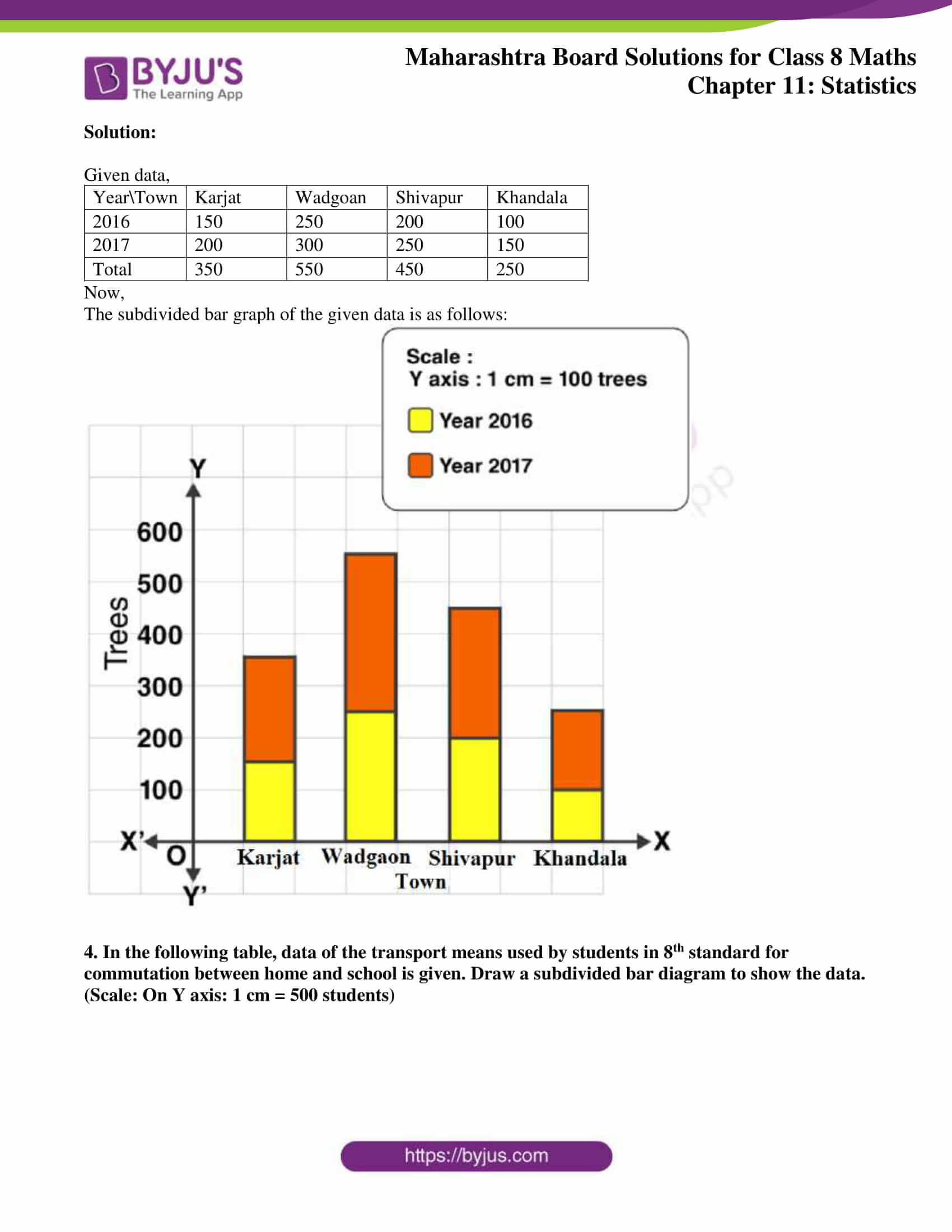
3. In the following table number of trees planted in the year 2016 and 2017 in four towns is given. Show the data with the help of subdivided bar graph.

Solution:
Given data,
| Year\Town | Karjat | Wadgoan | Shivapur | Khandala |
| 2016 | 150 | 250 | 200 | 100 |
| 2017 | 200 | 300 | 250 | 150 |
| Total | 350 | 550 | 450 | 250 |
Now,
The subdivided bar graph of the given data is as follows:

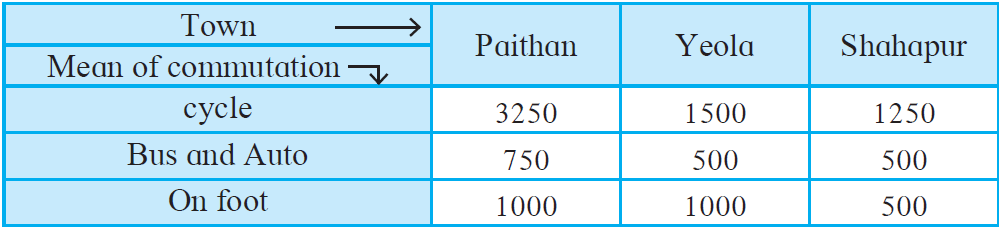
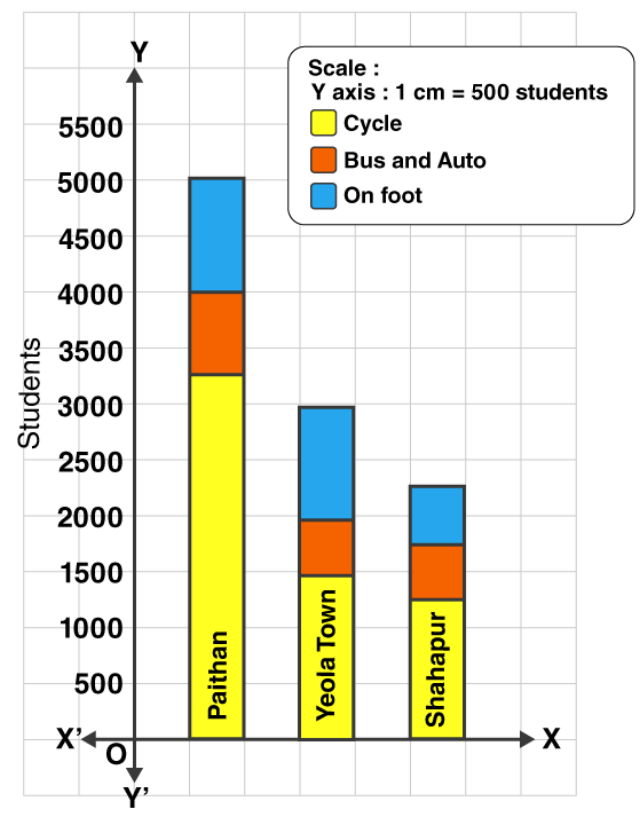
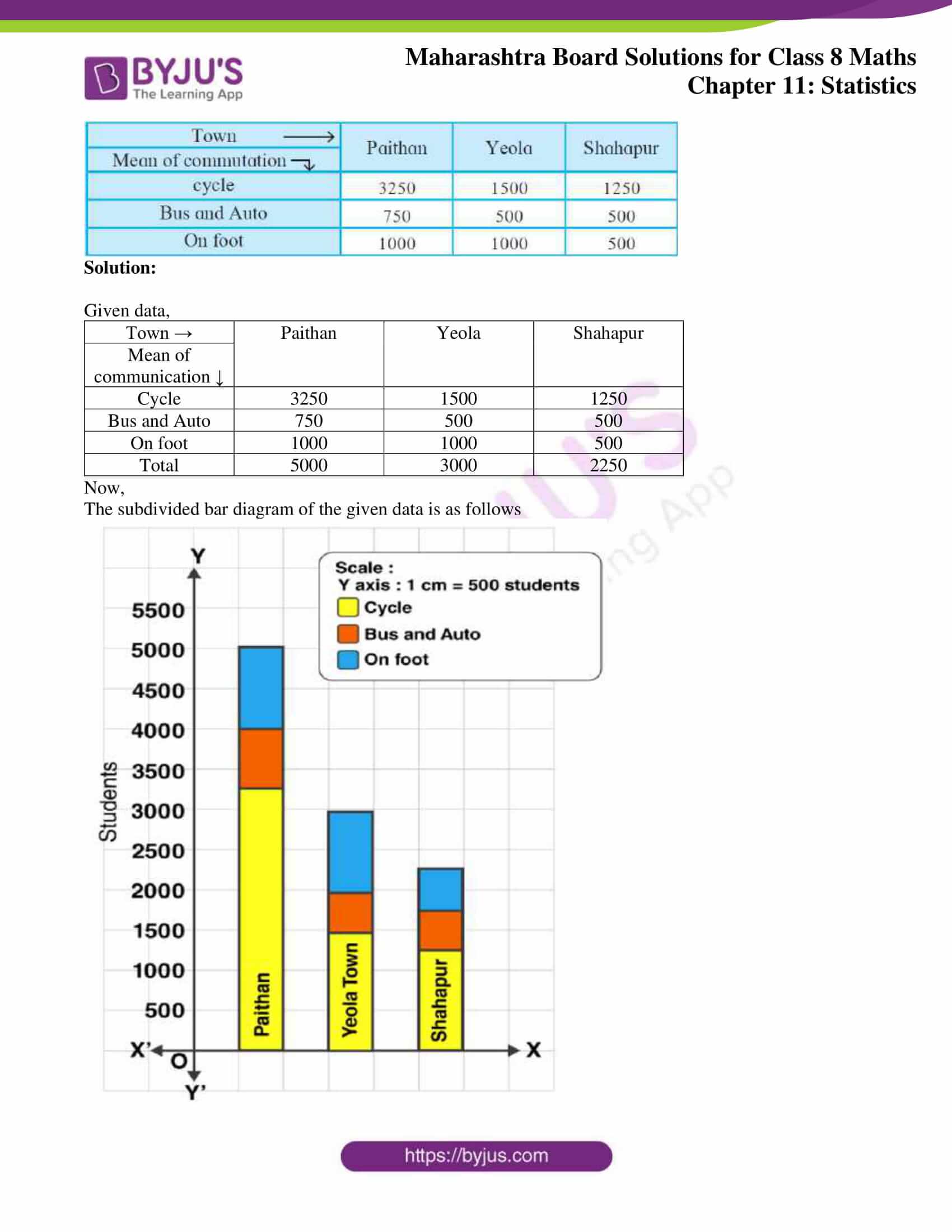
4. In the following table, data of the transport means used by students in 8th standard for commutation between home and school is given. Draw a subdivided bar diagram to show the data.
(Scale: On Y axis: 1 cm = 500 students)
Solution:
Given data,
| Town → | Paithan | Yeola | Shahapur |
| Mean of communication ↓ | |||
| Cycle | 3250 | 1500 | 1250 |
| Bus and Auto | 750 | 500 | 500 |
| On foot | 1000 | 1000 | 500 |
| Total | 5000 | 3000 | 2250 |
Now,
The subdivided bar diagram of the given data is as follows
Practice Set 11.3 Page No: 73
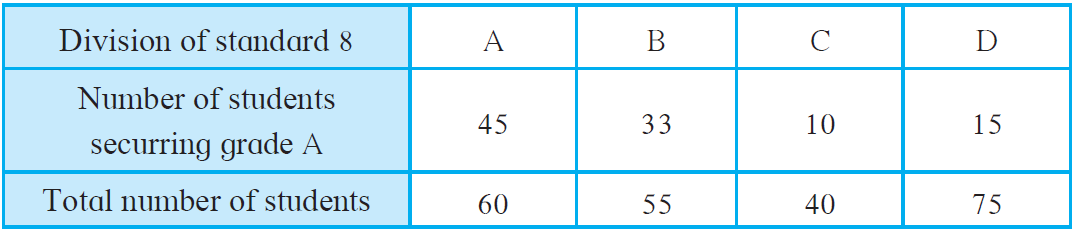
1. Show the following information by a percentage bar graph.
Solution:
Given data,
| Division of standard 8 | A | B | C | D |
| Number of students securing grade A | 45 | 33 | 10 | 15 |
| Total number of students | 60 | 55 | 40 | 75 |
| Percentage of students securing grade A | (45/60) x 100 = 75% | (33/55) x 100 = 60% | (10/40) x 100 = 25% | (15/75) x 100 = 20% |
Now, the percentage bar graph is:

2.

(1) State the type of the bar graph.
(2) How much percent is the Tur production to total production in Ajita’s farm?
(3) Compare the production of Gram in the farms of Yash and Ravi and state whose percentage of production is more and by how much?
(4) Whose percentage production of Tur is the least?
(5) State production percentages of Tur and gram in Sudha’s farm.
Solution:
From the given graph, it can be inferred that:
(1) The given graph is a percentage bar graph.
(2) Percent of tur production to the total production in Ajita’s farm is 60%.
(3) Production of Gram in the farm of Yash = 50%
And, the production of Gram in the farm of Ravi = 30%
So, the difference in the production = 50% – 30% =20%
Thus, Yash’s production of Gram is more and by 20%.
(4) The least production percentage of Tur is of Sudha.
(5) The production percentages of Tur and Gram in Sudha’s farm are 40% and 60% respectively.
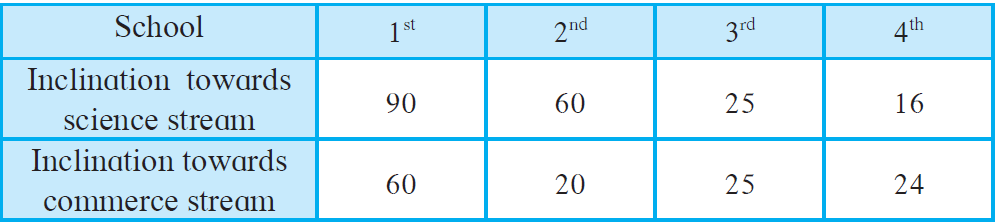
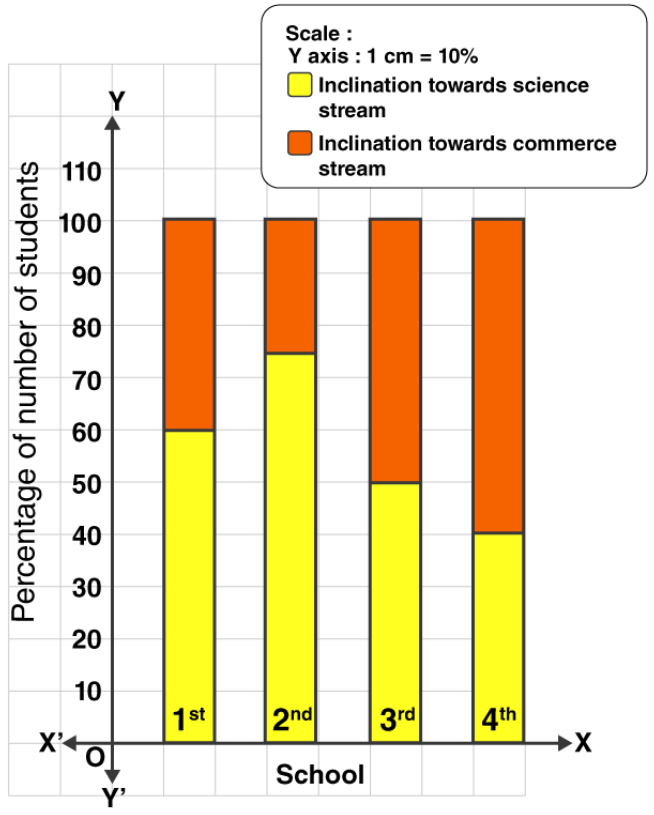
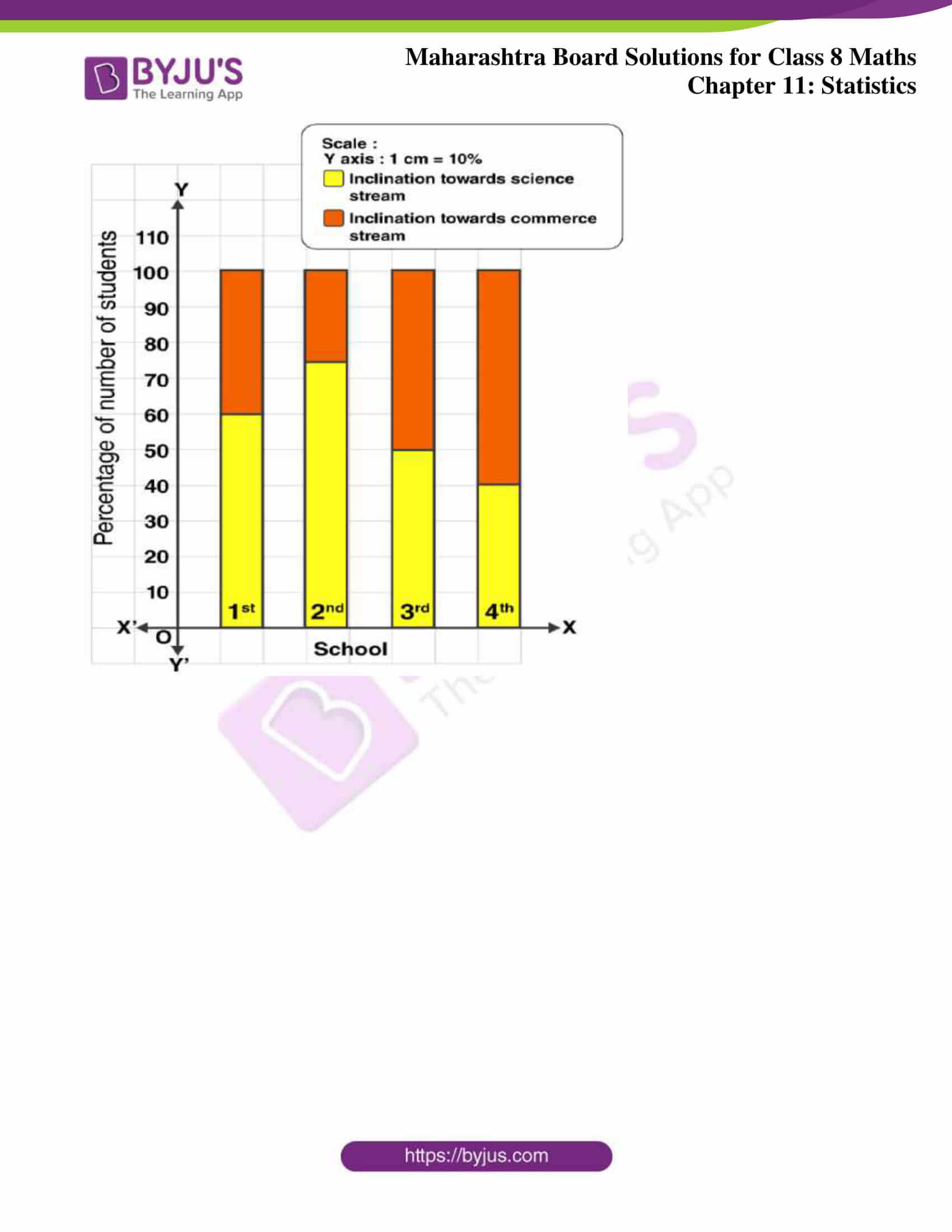
3. The following data is collected in a survey of some students of 10th standard from some schools. Draw the percentage bar graph of the data.
Solution:
Given data,
| School | 1st | 2nd | 3rd | 4th |
| Inclination towards science stream | 90 | 60 | 25 | 16 |
| Inclination towards commerce stream | 60 | 20 | 25 | 24 |
| Total | 150 | 80 | 50 | 40 |
| Percentage of students having inclination towards science stream | (90/150) x 100 = 60% | (60/80) x 100 = 75% | (25/50) x 100 = 50% | (16/40) x 100 = 40% |
| Percentage of students having inclination towards commerce stream | (60/150) x 100 = 40% | (20/80) x 100 = 25% | (25/50) x 100 = 50% | (24/40) x 100 = 60% |
The percentage bar graph of the given data is as follows:
Chapter 11 Statistics is one of the easy scoring chapters in Maharashtra board textbook for Class 8. We, at BYJU’S, provide useful resources for students to help scoring full marks in their examinations.
Our subject experts have solved the difficult problems with simpler steps in easy language, so that it’s understood by students of all levels. Regular revision of important concepts and formulas over time is the best way to strengthen concepts.
Frequently Asked Questions on Maharashtra State Board Solutions for Class 8 Maths Chapter 11 Statistics
What are the concepts explained in the Maharashtra State Board Class 8 Maths Chapter 11 Statistics Solutions?
These solutions help students to familiarize themselves with constructions of triangles. This chapter also deals with geometric constructions of triangles, if base, an angle adjacent to base and sum of lengths of two remaining sides are given.
How helpful are these Maharashtra State Board Class 8 Maths Chapter 11 Solutions?
Yes, these solutions are very helpful and Students are encouraged to practise these questions first. Then they can refer back to the solutions to analyse their performance. This will also help them to rectify the mistakes, so that they can avoid making any during the board exams. These solutions also lay the foundation for board exam questions.
Can these solutions be downloaded?
It is possible to download the solutions. We have provided the solutions as a scrollable PDF, and we have also mentioned the clickable link for the students to access. Meanwhile, we have also made these questions and the solutions available online on our webpage.







Comments