MSBSHSE Solutions For Class 8 Maths Part 2 Chapter 13 Congruence of triangles

MSBSHSE Solutions For Class 8 Maths Part 2 Chapter 13 Congruence of triangles are available here. Expert tutors at BYJU’S have created these solutions in order to help students with their exam preparations and thus, assisting them to acquire excellent marks in Maths. Students wishing to score higher marks should make use of the MSBSHSE Solutions for Class 8 while practising problems in the chapters of Maharashtra Board textbooks.

In this chapter, the main topics covered are understanding the congruence of triangles and their corresponding parts, proving two triangles are congruent by using any one of these: SSS, SAS, ASA, AAS (or SAA) and hypotenuse-side test. Solutions to all the exercise problems can easily be accessed by students from the PDF of Maharashtra Board Solutions for Class 8 Maths Chapter 13 Congruence of triangles, in the link provided below.

Download the PDF of Maharashtra Board Solutions For Class 8 Maths Part 2 Chapter 13 Congruence of triangles.

Access answers to Maharashtra Board Solutions For Class 8 Maths Part 2 Chapter 13 Congruence of triangles.

Practice Set 13.1 Page No: 85

1. In each pair of triangles in the following figures, parts bearing identical marks are congruent. State the test and correspondence of vertices by which triangles in each pair are congruent.

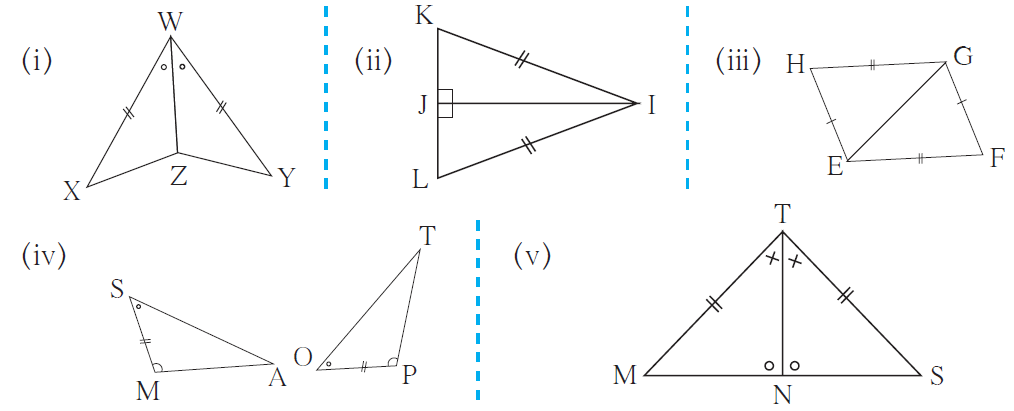
Solution:

(i) By SAS test, in the correspondence XWZ ↔ YWZ.

(ii) By Hypotenuse-side test, in the correspondence KJI ↔ LJI.

(iii) By SSS test, in the correspondence HEG ↔ FGE.

(iv) By ASA test, in the correspondence SMA ↔ OPT.

(v) By SAA test, in the correspondence MTN ↔ STN.

Practice Set 13.2 Page No: 87

1. In each pair of triangles given below, parts shown by identical marks are congruent. State the test and the one to one correspondence of vertices by which triangles in each pair are congruent and remaining congruent parts.

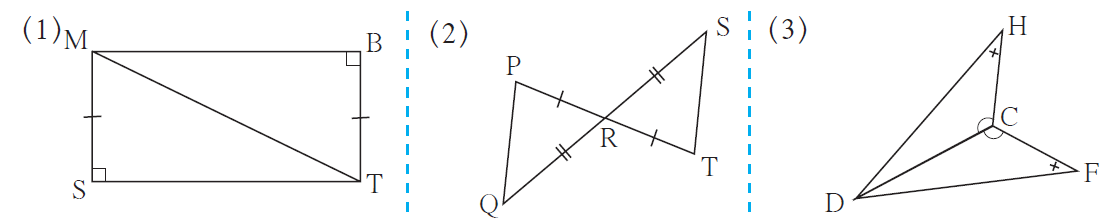
Solution:

(1)

In ∆MST and ∆TBM, we have

side MS ≅ side TB …. (given)

∠MST ≅ ∠TBM …. (right angle)

And, side MT is common

Hence, by Hypotenuse-side test ∆MST ≅ ∆TBM.

Now, from corresponding parts of congruent triangles

side ST ≅ side MB,

∠SMT ≅ ∠BTM,

∠STM ≅ ∠BMT.

(2)

In ∆PRQ and ∆TRS, we have

side PR ≅ side RT …. (given)

side QR ≅ side RS …. (given)

∠PRQ ≅ ∠SRT …. (vertically opposite angles)

Hence, by SAS test ∆PRQ ≅ ∆TRS.

Now, from corresponding parts of congruent triangles

side PQ ≅ side ST,

∠QPR ≅ ∠STR,

∠PQR ≅ ∠TSR.

(3)

In ∆DHC and ∆DFC, we have

∠DCH ≅ ∠DCF …. (given)

∠DHC ≅ ∠DFC …. (given)

And, side DC is common

Hence, by AAS test ∆DHC ≅ ∆DFC.

Now, from corresponding parts of congruent triangles

side DH ≅ side DF,

side HC ≅ side FC,

∠HDC ≅ ∠FDC.

2. In the adjacent figure, seg AD ≅ seg EC. Which additional information is needed to show that ΔABD and ΔEBC will be congruent by A-A-S test?

Solution:

In ∆ABD and ∆EBC, we have

side AD ≅ side EC … (given)

∠ABD ≅ ∠EBC … (vertically opposite angles)

Now,

In order to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test, one of the following is required:

∠BAD ≅ ∠BCE

or

∠BDA ≅ ∠BEC.

As the chapter is about Congruence of triangles, it’s a must for students to have a strong foundation over the concepts of this chapter, in order to tackle the higher grades. Regular revision of important concepts is the best way to strengthen the concepts. Further, it is recommended that students go through the solutions on a daily basis to improve their performance in the examination.