MSBSHSE Solutions For Class 8 Maths Part 2 Chapter 15 Area

MSBSHSE Solutions For Class 8 Maths Part 2 Chapter 15 Area is one of the best resources available for free, which students can rely on. The MSBSHSE Solution for Class 8 contains all the important concepts, which are essential for students to score well in the examinations. Individual subject matter experts have created these solutions accurately, depending upon the understanding capabilities of students of all levels. Every question is solved in a stepwise approach to provide a better interpretation of the problem for the students.

The best guide for the students is the Maharashtra State Board Class 8 Textbooks Maths Solutions. On referring to these solutions, students can analyse their weak areas and can improve on it by thoroughly analysing the solutions once again. Some of the important topics covered in this chapter are area of a parallelogram, area of a trapezium, area of a rhombus, area of a triangle using Heron’s formula and area of a circle. Students can access the PDF of Maharashtra Board Solutions for Class 8 Maths Chapter 15 Area, from the link given below.

Download the PDF of Maharashtra Board Solutions For Class 8 Maths Part 2 Chapter 15 Area

Access answers to Maharashtra Board Solutions For Class 8 Maths Part 2 Chapter 15 Area.

Practice Set 15.1 Page No: 95

1. If base of a parallelogram is 18 cm and its height is 11 cm, find its area.

Solution:

Given,

Base of parallelogram = 18 cm and it’s height = 11 cm

Area of parallelogram = Base x height

= 18 x 11

= 198 sq. cm

Thus, the area of the parallelogram is 198 sq. cm.

2. If area of a parallelogram is 29.6 sq cm and its base is 8 cm, find its height.

Solution:

Given,

Area of parallelogram = 29.6 sq.cm

Base of parallelogram = 8 cm

We know that,

Area of parallelogram = base x height

⇒ 29.6 = 8 x height

Height = 29.6/8 = 3.7 cm

Thus, the height of the parallelogram is 3.7 cm.

3. Area of a parallelogram is 83.2 sq. cm. If its height is 6.4 cm, find the length of its base.

Solution:

Given,

Area of parallelogram = 83.2 sq. cm

Height of the parallelogram = 6.4 cm

We know that,

Area of parallelogram = base x height

⇒ 83.2 = base x 6.4

Base = 83.2/6.4 = 13 cm

Thus, the base of parallelogram is 13 cm.

Practice Set 15.2 Page No: 97

1. Lengths of the diagonals of a rhombus are 15 cm and 24 cm, find its area.

Solution:

Given,

Lengths of the diagonals of a rhombus are 15 cm and 24 cm.

Area of rhombus = ½ x product of diagonals

= ½ x (15 x 24)

= 15 x 12

= 180 sq. cm

Thus, the area of the rhombus is 180 sq. cm

2. Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm, find its area.

Solution:

Given,

Lengths of the diagonals of a rhombus are 16.5 cm and 14.2 cm.

Area of rhombus = ½ x product of diagonals

= ½ x (16.5 x 14.2)

= 16.5 x 7.1

= 117.15 sq. cm

Thus, the area of the rhombus is 117.15 sq. cm

3. If perimeter of a rhombus is 100 cm and length of one diagonal is 48 cm, what is the area of the quadrilateral?

Solution:

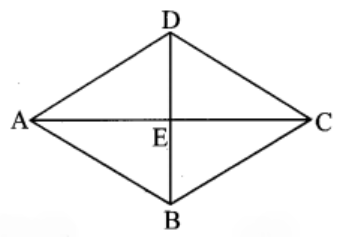Given,

Perimeter of a rhombus = 100 cm

Length of one diagonal = 48 cm

Let’s consider ABCD to be the rhombus. AC and BD are the diagonals which intersect at point E.

So, l(AC) = 48 cm

And, we know

l(AE) = ½ l(AC) [As diagonals of a rhombus bisect each other]

= ½ x 48

= 24 cm

Now, the perimeter of rhombus = 4 x side

⇒ 100 = 4 x l(AB)

l(AB) = 100/4 = 25 cm

Next in ∆ ABE, we have

m ∠AED = 90^o [As diagonals of a rhombus bisect each other at right angles]

By using Pythagoras theorem,

l(AB)² = l(EB)² + l(AE)²

(25)² = l(EB)² + (24)²

625 = l(EB)² + 576

l(EB)² = 635 – 576 = 49

l(EB) = √49 = 7 cm (Taking square root on both the sides)

Now,

l(EB) = ½ x l(BD) [As diagonals of a rhombus bisect each other]

l(BD) = 2 x l(EB)

= 2 x 7 = 14 cm

So,

Area of the rhombus = ½ x product of lengths of diagonals

= ½ x l(AC) x l(BD)

= ½ x 48 x 14

= 48 x 7 = 336 sq. cm

Thus, the area of the rhombus is 336 sq. cm.

4. If length of a diagonal of a rhombus is 30 cm and its area is 240 sq. cm, find its perimeter.

Solution:

Given,

Length of a diagonal of a rhombus = 30 cm and it’s area = 240 sq. cm.

Let’s consider ABCD to be the rhombus having AC and BD as the diagonals and the diagonals intersect at point E.

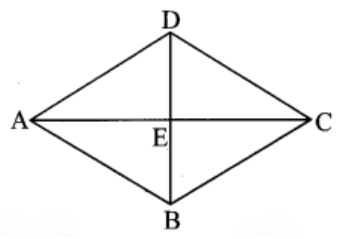⇒ l(AC) = 30 cm

Area of rhombus = ½ x Product of lengths of diagonals

240 = ½ x l(AC) x l(BD)

240 = ½ x 30 x l(BD)

240 = 15 x l(BD)

l(BD) = 240/15 = 16 cm

We know that the diagonals of a rhombus bisect each.

So,

l(AE) = ½ x l(AC) = ½ x 30 = 15 cm

And,

l(DE) = ½ x l(BD) = ½ x 16 = 8 cm

Now, in ∆ ADE

m ∠AED = 90^o [As diagonals of a rhombus bisect each other at right angles]

By Pythagoras Theorem, we have

l(AD)² = l(AE)² + l(DE)²

l(AD)² = (15)² + (8)²

= 225 + 64 = 289

l(AD) = 289 = 17 cm

So, the perimeter of the rhombus = 4 x side

= 4 x AD

= 4 x 17 = 68 sq. unit

Thus, the perimeter of the rhombus is 68 cm.

Practice Set 15.3 Page No: 95

1. In □ ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of □ ABCD.

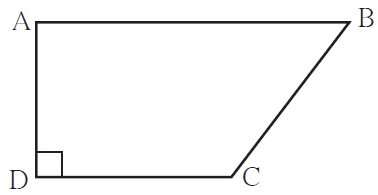
Solution:

Given, ABCD is a trapezium and side AB || side DC

l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm.

Area of trapezium = ½ x sum of lengths of parallel sides x height

= ½ x [l(AB) + l(DC)] x l(AD)

= ½ x [13 + 9] x 8

= ½ x 22 x 8

= 11 x 8 = 88 cm

Thus, the area of the trapezium ABCD is 88 sq. cm.

2. Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm respectively and its height is 4.2 cm, find its area.

Solution:

Given,

Length of the two parallel sides of a trapezium are 8.5 cm and 11.5 cm and it’s height is 4.2 cm.

We know that,

Area of trapezium = ½ x sum of lengths of parallel sides x height

= ½ x [8.5 + 11.5] x 4.2

= ½ x 20 x 4.2

= 10 x 4.2 = 42 sq. cm

Thus, the area of the trapezium is 42 sq. cm.

3. □ PQRS is an isosceles trapezium l(PQ) = 7 cm. seg PM ⊥ seg SR, l(SM) = 3 cm, Distance between two parallel sides is 4 cm, find the area of □ PQRS.

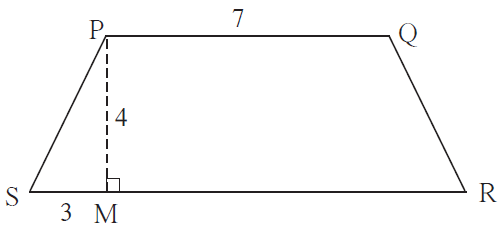
Solution:

Given,

An isosceles trapezium PQRS, l(PQ) = 7 cm. seg PM ⊥ seg SR, l(SM) = 3 cm.

And, the distance between two parallel sides = 4 cm.

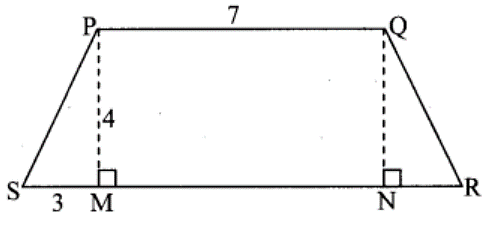
Let’s draw seg QN ⊥ seg SR.

Now, in □ PMNQ we have

seg PQ || seg MN

∠PMN = ∠QNM = 90^o

Hence, □ PMNQ is a rectangle.

So, l(PM) = l(QN) = 4cm and l(PQ) = l(MN) = 7 cm [Opposite sides of a rectangle]

In ∆ PMS, we have

m ∠PMS = 90^o

So, by Pythagoras theorem

l(PS)² = l(PM)² + l(SM)²

= 4² + 3²

= 16 + 9 = 25

l(PS) = √25 = 5 cm [Taking square root on both sides]

Now, as □ PQRS is an isosceles trapezium

l(PS) = l(QR) = 5 cm

In ∆ QNR, we have

m ∠QNR = 90^o

So, by Pythagoras theorem

l(QR)² = l(QN)² + l(NR)²

5² = 4² + l(NR)²

25 = 16 + l(NR)²

l(NR)² = 25 – 16 = 9

l(NR) = √9 = 3 cm [Taking square root on both sides]

So, l(SR) = l(SM) + l(MN) + l(NR) = 3 + 7 + 3 = 13 cm

Area of trapezium = ½ x sum of lengths of parallel sides x height

= ½ x [l(PQ) + l(SR) x l(PM)]

= ½ x [7 + 13] x 4

= ½ x 20 x 4

= 10 x 4 = 40 sq. cm

Therefore, the area of trapezium PQRS is 40 sq. cm.

Practice Set 15.4 Page No: 101

1. Sides of a triangle are cm 45 cm, 39 cm and 42 cm, find its area.

Solution:

Given,

Sides of a triangle are 45 cm, 39 cm and 42 cm.

By Heron’s formula

Here, a = 45cm, b = 39cm, c = 42cm

Semi perimeter of triangle = s = ½ (a + b + c)

s = ½ x (45 + 39 + 42)

s = ½ x 126 = 63

Now, the area of triangle is

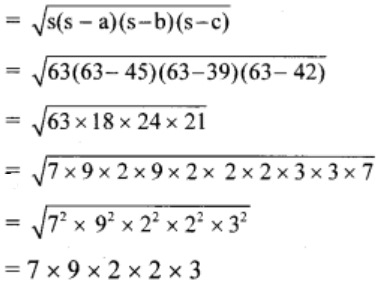
= 756 sq. cm

Therefore, the area of the triangle is 756 sq. cm.

2. Look at the measures shown in the adjacent figure and find the area of □ PQRS.

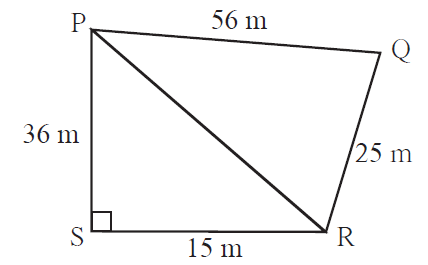
Solution:

From the given figure, its seen that

Area(□ PQRS) = Area(∆ PSR) + Area(∆ PQR)

Now, in ∆ PSR we have

l(PS) = 36 m and l(SR) = 15 m

Area(∆ PSR) = ½ x base x height

= ½ x l(SR) x l(PS)

= ½ x 15 x 36

= 270 sq. m

In right ∆ PSR, we have

By Pythagoras theorem,

l(PR)² = l(PS)² + l(SR)²

= 36² + 15²

= 1296 + 225 = 1521

l(PR) = √1521 = 39 m [Taking square root both the sides]

Now,

In ∆PQR, a = 56m, b = 25m, c = 39m

So, the semi-perimeter = ½ x (a + b + c)

= ½ x (56 + 25 + 39)

= 120/2 = 60 m

Hence, the area of ∆PQR is

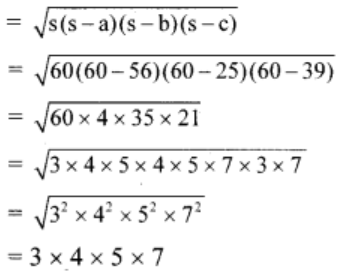
= 420 sq. m

Therefore, the area of Area(□ PQRS) = 270 + 420 = 690 sq. m

3. Some measures are given in the adjacent figure, find the area of □ ABCD.

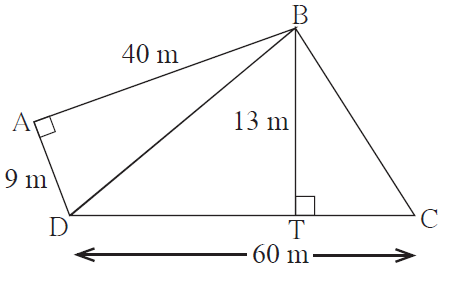
Solution:

From the given figure, it’s seen that

Area(□ ABCD) = Area(∆ BAD) + Area(∆ BDC)

Now, in ∆ BAD we have

m ∠BAD = 90°, l(AB) = 40 m, l(AD) = 9 m

Area(∆ BAD) = ½ x base x height

= ½ x 9 x 40 = 9 x 20

= 180 sq. m

Next, in ∆BDC, l(BT) = 13 m, l(CD) = 60 m

Area(∆ BDC) = ½ x base x height

= ½ x l(CD) x l(BT)

= ½ x 60 x 13 = 30 x 13

= 390 sq. m

Hence,

Area(□ ABCD) = Area(∆ BAD) + Area(∆ BDC)

= 180 + 390 = 570 sq. m

Therefore, the area of □ ABCD is 570 sq. m.

Practice Set 15.5 Page No: 102

1. Find the areas of given plots. (All measures are in metres.)

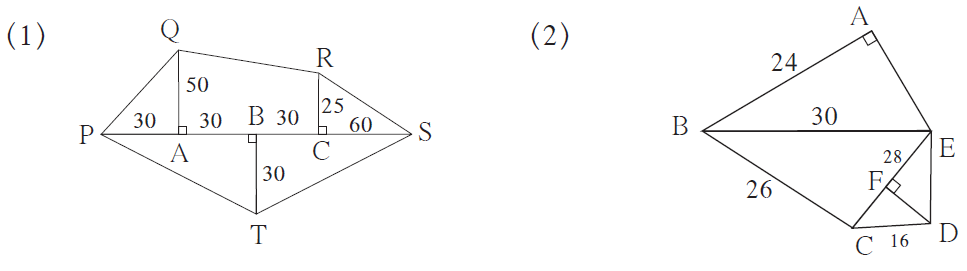
Solution:

(1) From the given figure it’s seen that,

∆QAP, ∆RCS are right angled triangles and □ QACR is a trapezium.

In ∆QAP, l(AP) = 30 m, l(QA) = 50 m

A(∆QAP) = ½ x product of sides forming the right angle

= ½ x l(AP) x l(QA)

= ½ x 30 x 50

= 750 sq. m

In □ QACR, we have

l(QA) = 50 m, l(RC) = 25 m,

l(AC) = l(AB) + l(BC)

= 30 + 30 = 60 m

Now, A(□QACR) = 12 x sum of lengths of parallel sides x height

= 12 x [l(QA) + l(RC)] x l(AC)

= 12 x (50 + 25) x 60

= 12 x 75 x 60

= 2250 sq.m

Next, in ∆RCS we have

l(CS) = 60 m, l(RC) = 25 m

A(∆RCS) = ½ x product of sides forming the right angle

= ½ x l(CS) x l(RC)

= ½ x 60 x 25

= 750 sq. m

And, in ∆PTS, we have

l(TB) = 30 m,

l(PS) = l(PA) + l(AB) + l(BC) + l(CS)

= 30 + 30 + 30 + 60

= 150m

So, A(∆PTS) = ½ x base x height

= 12 x l(PS) x l(TB)

= 12 x 150 x 30

= 2250 sq. m

Hence,

Area of plot QPTSR = A(∆QAP) + A(₹QACR) + A(∆RCS) + A(∆PTS)

= 750 + 2250 + 750 + 2250

= 6000 sq. m

Therefore, the area of the given plot is 6000 sq. m.

(2) In ∆ABE, we have

m ∠BAE = 90°, l(AB) = 24 m, l(BE) = 30 m

By Pythagoras theorem,

(30)² = (24)² + [l(AE)]²

900 = 576 + [l(AE)]²

l(AE) = √324 = 18 m [Taking square root of both sides]

Now,

A(∆ABE) = 12 x product of sides forming the right angle

= 12 x l(AE) x l(AB)

= 12 x 18 x 24

= 216 sq. m

Next,

In ∆BCE, a = 30 m, b = 28 m, c = 26 m

Semi-perimeter of ∆BCE (s) = ½ x (a + b + c)

= ½ x (30 + 28 + 26)

= ½ x 84 = 42 m

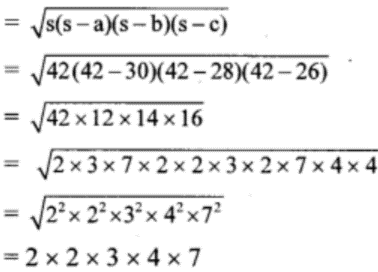So,

A(∆BCE)

= 336 sq. m

And,

In ∆EDC, we have

l(CE) = 28 m, l(DF) = 16 m

A(∆EDC) = ½ x base x height

= ½ x l(CE) x l(DF)

= ½ x 28 x 16 = 224 sq. m

Thus,

Area of plot ABCDE = A(∆ABE) + A(∆BCE) + A(∆EDC)

= 216 + 336 + 224 = 776 sq. m

Therefore, the area of the given plot is 776 sq. m.

Practice Set 15.6 Page No: 104

1. Radii of the circles are given below, find their areas.

(1) 28 cm (2) 10.5 cm (3) 17.5 cm

Solution:

(1) Given,

Radius of the circle (r) = 28 cm

Area of the circle = πr²

= 22/7 x (28)²

= 22/7 x 28 x 28

= 22 x 4 x 28

= 2464 sq. cm

(2) Given,

Radius of the circle (r) = 10.5 cm

Area of the circle = πr²

= 22/7 x (10.5)²

= 22/7 x 10.5 x 10.5

= 22 x 1.5 x 10.5

= 346.5 sq. cm

(3) Given,

Radius of the circle (r) = 17.5 cm

Area of the circle = πr²

= 22/7 x (17.5)²

= 22/7 x 17.5 x 17.5

= 22 x 2.5 x 17.5

= 962.5 sq. cm

2. Areas of some circles are given below find their diameters.

(1) 176 sq. cm (2) 394.24 sq. cm (3) 12474 sq. cm

Solution:

(1) Given,

Area of the circle =176 sq. cm

Area of the circle = πr²

⇒176 = 22/7 x r²

r² = (176 x 7)/ 22

r² = 56

r = √56 cm [Taking square root of both sides]

Hence, the diameter = 2r = 2√56 cm

(2) Given,

Area of the circle = 394.24 sq. cm

Area of the circle = πr²

⇒ 394.24 = 22/7 x r²

r² = (394.24 x 7)/ 22

r² = 39424 x (7/2200)

r² = (1792/100) x 7

r² = 12544/100

r² = 112²/10²

r = 112/10 = 11.2 cm [Taking square root of both sides]

Hence, the diameter = 2r = 2 x 11.2 = 22.4 cm

(3) Given,

Area of the circle = 12474 sq. cm

Area of the circle = πr²

⇒ 12474 = 22/7 x r²

r² = (12474 x 7)/ 22

r² = 567 x 7

r² = 3969

r = 63 cm [Taking square root of both sides]

Hence, the diameter = 2r = 2 x 63 = 126 cm

3. Diameter of the circular garden is 42 m. There is a 3.5 m wide road around the garden. Find the area of the road.

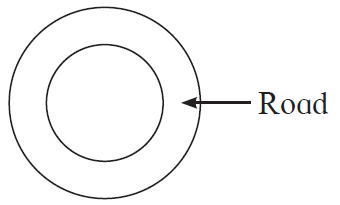
Solution:

Given,

Diameter of the circular garden is 42 m.

⇒ Radius of the circular garden (r) = 422 = 21 m

Width of the road = 3.5 m

So, radius of the outer circle (R) = radius (r) + width of the road

= 21 + 3.5

= 24.5 m

Area of the road = area of outer circle – area of circular garden

= πR² – πr²

= π (R² – r²)

= 22/7 [(24.5)² – (21)²]

= 22/7 (24.5 + 21) (24.5 – 21) [As a²-b² = (a+b) (a-b)]

= 227 x 45.5 x 3.5

= 22 x 45.5 x 0.5

= 500.50 sq. m

Therefore, the area of the road is 500.50 sq. m.

4. Find the area of the circle if its circumference is 88 cm.

Solution:

Given,

Circumference of the circle = 88 cm

Circumference of the circle = 2πr

⇒ 88 = 2 x 227 x r

r = 88 × 72 × 22

∴ r = 14cm

Area of the circle = πr² = 22/7 x (14)²

= 227 x 14 x 14 = 22 x 2 x 14 = 616 sq. cm

Therefore, the area of circle is 616 sq. cm.

Finding the area of different shapes has many applications in the real world. By practising the exercise problems using the solutions, students can secure good marks in their exams. Further, students can depend on this resource to comprehend all the other chapters of the textbook completely. Stay tuned to learn more about Area, MSBSHSE exam pattern and other information.