In Geometry, a shape is defined as the figure closed by the boundary. The boundary is created by the combination of lines, points and curves. Basically, there are two different types of geometric shapes such as:
- Two – Dimensional Shapes
- Three – Dimensional Shapes
Each and every shape in the Geometry can be measured using different measures such as area, volume, surface area, perimeter and so on. In this article, let us discuss the area of shapes for 2D figures and 3D figures with formulas.
Table of Contents:
What is Area?
An area is a quantity that expresses the extent of a two-dimensional figure or shape or planar lamina in the plane. Lamina shapes include 2D figures that can be drawn on a plane, e.g., circle, square, triangle, rectangle, trapezium, rhombus and parallelogram. Area of shapes such as circle, triangle, square, rectangle, parallelogram, etc. are the region occupied by them in space.
Polygon shape: A polygon is a two-dimensional shape that is formed by straight lines. The examples of polygons are triangles, hexagons and pentagons. The names of shapes describe how many sides exist in the shape. For instance, a triangle consists of three sides and a rectangle has four sides. Hence, any shape that can be formed using three straight lines is known as a triangle and any shape that can be drawn by linking four lines is known as a quadrilateral. The area is the region inside the boundary/perimeter of the shapes which is to be considered.
What are 2D shapes?
The two-dimensional shapes (2D shapes) are also known as flat shapes, are the shapes having two dimensions only. It has length and breadth. It does not have thickness. The two different measures used for measuring the flat shapes are area and the perimeter. Two-dimensional shapes are the shapes that can be drawn on the piece of paper. Some of the examples of 2D shapes are square, rectangle, circle, triangle and so on.
Area of 2D Shapes Formula
In general, the area of shapes can be defined as the amount of paint required to cover the surface with a single coat. Following are the ways to calculate area based on the number of sides that exist in the shape, as illustrated below in the fig.
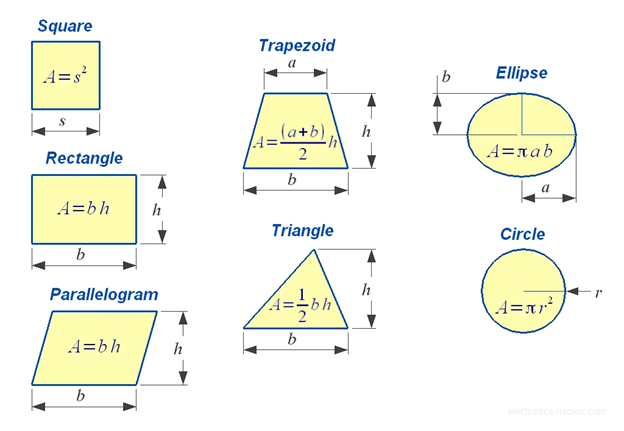
Let us write the formulas for all the different types of shapes in a tabular form.
| Shape | Area | Terms |
| Circle | π × r2 | r = radius of the circle |
| Triangle | ½ × b × h | b = base
h = height |
| Square | a2 | a = length of side |
| Rectangle | l × w | l = length
w = width |
| Parallelogram | b × h | b=base
h=vertical height |
| Trapezium | ½(a+b) × h | a and b are the length of parallel sides
h = height |
| Ellipse | πab | a = ½ minor axis
b = ½ major axis |
Also, read:
What are 3D shapes?
The three-dimensional shapes (3D shapes), known as solid shapes, are the shapes that have three dimensions such as length, breadth and thickness. The two distinct measures used to define the three-dimensional shapes are volume and surface area. Generally, the three-dimensional shapes are obtained from the rotation of two-dimensional shapes. Thus, the surface area of any 2D shapes should be a 2D shape. If you want to calculate the surface area of solid shapes, we can easily calculate from the area of 2D shapes.
Area of 3D Shapes Formula
According to the International System of Units (SI), the standard unit of area is the square meter (written as m2) and is the area of a square whose sides are one meter long. For example, a particular shape with an area of three square meters would have the same area as three such squares. The surface area of a solid object is a measure of the total area that the surface of the object occupies.
For 3D/ solid shapes like cube, cuboid, sphere, cylinder and cone, the area is updated to the concept of the surface area of the shapes. The formulas for three-dimension shapes are given in the table here:
| Shape | Surface area | Terms |
| Cube | 6a2 | a = length of the edge |
| Rectangular prism | 2(wl+hl+hw) | l = length
w = width h = height |
| Cylinder | 2πr(r + h) | r = radius of circular base
h = height of the cylinder |
| Cone | πr(r + l) | r = radius of circular base
l = slant height |
| Sphere | 4πr2 | r = radius of sphere |
| Hemisphere | 3πr2 | r = radius of hemisphere |
In addition to the area of the planar shapes, an additional variable i.e the height or the radius are taken into account for computing the surface area of the shapes.
Consider a circle of radius r and make endless concentric circles. Now from the centre to the boundary make a line segment equal to the radius and cut the figure along with that segment. It’ll be formed a triangle with base equal to the circumference of the circle and height is equal to the radius of the outer circle, i.e., r. The area can thus be calculated as ½ * base * height i.e
Area of Shapes Examples
Example 1:
Find the area of the circular path whose radius is 7m.
Solution:
Given, radius of circular path, r = 7m
By the formula of area of circle, we know;
A = π r2
A = 22/7 x 7 x 7
A = 154 sq.m.
Example 2:
The side-length of a square plot is 5m. Find the area of a square plot.
Solution:
Given, side length, a = 5m
By the formula of area of a square, we know;
Area = a2
A = 5 x 5
A = 25 sq.m.
Example 3:
Find the area of the cone, whose radius is 4cm and height is 3cm.
Solution:
Given, radius of cone = 4cm
and height of cone = 3cm.
As per the formula of area of cone, we know;
Slant height =l = √(42 + 32) = √25 = 5 cm
Area = πr(r + l)
= (22/7) × 4(4 + 5)
=(22/7) 36
= 113. 14 cm2
To learn more Maths-related articles, stay tuned with BYJU’S – The Learning App and download the app to learn with ease by exploring more videos.

this was very hepful
This was a greatful
A very good website I got almost all i was looking for
hi my name is Joannah Jokthan and I want to join this program
Thank you for these examples; area of shapes with 3D shapes .
found this page really helpful.
This is very helpful and I am looking forward to join your school. I get all I am looking for in your program. Thank you for the area definition, 2d and 3d shapes, area of 2d and 3d shapes and the examples they were really helpful. Thanks BYJU’S the learning app. Thanks.