NCERT Solution Class 12 Chapter 13 - Probability Exercise 13.1

NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.1 – Free PDF Download

Exercise 13.1 of NCERT Solutions for Class 12 Maths Chapter 13 – Probability is based on the following topics:

1. Introduction
2. Conditional Probability
   1. Properties of conditional probability: There are 3 properties of conditional probability that are explained in the chapter.

Solving the problems in this exercise will help the students understand why these properties are important, as well as about the implementation of these properties while solving the questions.

NCERT Solutions for Class 12 Maths Chapter 13 – Probability Exercise 13.1

Download PDF

carouselExampleControls112

Previous





Next

Access Other Exercises of Class 12 Maths Chapter 13

Exercise 13.2 Solutions 18 Questions

Exercise 13.3 Solutions 14 Questions

Exercise 13.4 Solutions 17 Questions

Exercise 13.5 Solutions 15 Questions

Miscellaneous Exercise On Chapter 13 Solutions 10 Questions

Access Answers to NCERT Class 12 Maths Chapter 13 Exercise 13.1

1. Given that E and F are events such that P (E) = 0.6, P (F) = 0.3 and P (E ∩ F) = 0.2, find P (E|F) and P (F|E).

Solution:

2. Compute P (A|B), if P (B) = 0.5 and P (A ∩ B) = 0.32.

Solution:

3. If P (A) = 0.8, P (B) = 0.5 and P (B|A) = 0.4, find
(i) P (A ∩ B)

(ii) P (A|B)

(iii) P (A ∪ B)

Solution:

4. Evaluate P (A ∪ B), if 2P (A) = P (B) = 5/13 and P (A|B) = 2/5.

Solution:

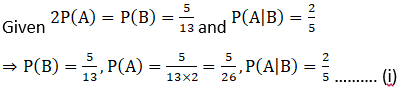
5. If P (A) = 6/11, P (B) = 5/11 and P (A ∪ B) = 7/11, find
(i) P (A∩B)

(ii) P (A|B)

(iii) P (B|A)

Solution:

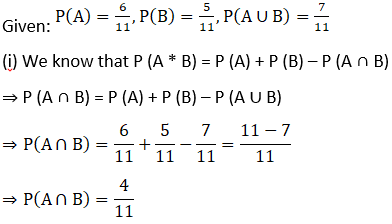
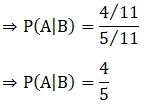
Determine P (E|F) in Exercises 6 to 9.

6. A coin is tossed three times, where
(i) E : head on third toss, F : heads on first two tosses
(ii) E : at least two heads, F : at most two heads
(iii) E : at most two tails, F : at least one tail

Solution:

7. Two coins are tossed once, where
(i) E: tail appears on one coin, F: one coin shows head
(ii) E: no tail appears, F: no head appears

Solution:

(ii) Here, E: no tail appears

And F: no head appears

⇒ E = {HH} and F = {TT}

⇒ E ∩ F = ϕ

8. A die is thrown three times, E: 4 appears on the third toss, F: 6 and 5 appears respectively on the first two tosses.

Solution:

9. Mother, father and son line up at random for a family picture
E: son on one end, F: father in middle

Solution:

Let M denote mother, F denote father and S denote son.

Then, the sample space for the given experiment will be:

S = {MFS, SFM, FSM, MSF, SMF, FMS}

Here, E: Son on one end

And F: Father in middle

⇒ E = {MFS, SFM, SMF, FMS} and F = {MFS, SFM}

⇒ E ∩ F = {MFS, SFM}

10. A black and a red dice are rolled.
(a) Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
(b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.

Solution:

11. A fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and G = {2,3,4,5}
Find
(i) P (E|F) and P (F|E)
(ii) P (E|G) and P (G|E)
(iii) P ((E ∪ F)|G) and P ((E ∩ F)|G)

Solution:

(iii) Clearly, from (i), we have

E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5}

⇒ E ∪ F = {1, 2, 3, 5}

⇒ (E ∪ F) ∩ G = {2, 3, 5}

12. Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that (i) the youngest is a girl, (ii) at least one is a girl?

Solution:

Let B denote boy and G denote girl.

Then, the sample space of the given experiment is S = {GG, GB, BG, BB}

Let E be the event that ‘both are girls’.

13. An instructor has a question bank consisting of 300 easy True / False questions, 200 difficult True / False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple choice question?

Solution:

Here, there are two types of questions, True/False or Multiple Choice Questions (T/F or MCQ), and each of them are divided into Easy and Difficult type, as shown below in the tree diagram.

14. Given that the two numbers appearing on throwing two dice are different. Find the probability of the event ‘the sum of numbers on the dice is 4’.

Solution:

15. Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event ‘the coin shows a tail’, given that ‘at least one die shows a 3’.

Solution:

16. If P (A) = 1/2, P (B) = 0, then P (A|B) is
A. 0
B. ½
C. not defined
D. 1

Solution:

C. Not defined

Explanation:

17. If A and B are events such that P (A|B) = P (B|A), then
A. A ⊂ B but A ≠ B
B. A = B
C. A ∩ B = φ
D. P (A) = P (B)

Solution:

D. P (A) = P (B)

Explanation:

Also, explore –

NCERT Solutions for Class 12 Maths

NCERT Solutions for Class 12

NCERT Solutions