What does Bell Theorem mean?
Bell’s theorem states that
“There is no physical theory for local hidden variables which can reproduce the quantum mechanics predictions”.
The theorem is named after John Stewart Bell. Hidden variables are the microscopic properties of particles that are difficult to observe with the existing microscope. However, according to the Heisenberg Uncertainty Principle, these variables do not exist outside the context of observation.
Bell’s Theorem Formula
According to the theorem if X, Y and Z are the photon measurement variables then,
| P (X = Y) + P (Y = Z) + P (Z = X) ≥ 1 |
where P(X=Y) is the probability of X = Y, which is mathematically relevant.
What is Bell’s Inequality?
Bell’s inequality can be best explained with the help of quantum mechanics. In quantum mechanics, it is believed that when electrons are sent across the magnetic field, half of the electrons get deflected towards the right and the other half to the left. The right half of the electrons are again sent across another magnetic field perpendicular to the first; then they split into half so that few go up and the other few go down. This is known as the randomness of the electron, which is studied using Bell’s theorem.
What is Local Realism?
Local realism is a concept that is formalized to state and prove Bell’s theorem with Alice and Bob (the outcome of random sampling). Alice and Bob observed two observed values with detector settings: A(a,λ), and b is B(b,λ), respectively.
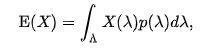
Above is the expression of local realism.
Example of Bell’s Theorem
Photon polarisation: Polarisation of light is the example that explains Bell’s theorem and Bell’s inequality as it involves the study of particles.
Frequently Asked Questions – FAQs
State Bells Theorem
Who stated Bells theorem?
Give an example of Bells theorem.
What is Bell Experiment?
What is Local Realism?
Related Articles:
| Electromagnetic Radiation | Electromagnetism |
| Magnetic Field And Magnetic Field Lines | Entropy & Second Law Of Thermodynamics |
Stay tuned to BYJU’S and Fall in Love with Learning!
Why is there space between particles?


Comments