As we know, the rotational motion and translational motion are analogous to each other in any respect. Also, the terms we use in rotational motion such as the angular velocity and angular acceleration as analogous to the terms velocity and acceleration in translational motion. In that respect, we see that the rotation of a body about a fixed axis is analogous to the linear motion of a body in translational motion. In this section, we will discuss the kinematics of a body undergoing rotational motion about a fixed axis.
| Table of Contents |
Angular Velocity
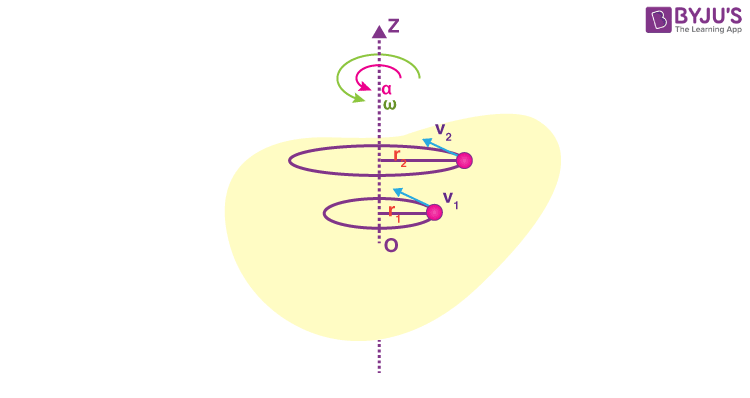
Let us consider an object undergoing rotational motion about a fixed axis, as shown in the figure. Let us take a particle P on the rotating object. When the object rotates about the axis passing through O, the particle P displaces from one point to another, such that, the angular displacement of the particle is “Ɵ”.
- We can say that, at time t = 0, the angular displacement of the particle P is 0 and at time t, its angular displacement is equal to Ɵ.
- Now, the rate of change of angular displacement with time is termed as the angular velocity of the particle.
- Mathematically, angular velocity \(\begin{array}{l}\omega = \frac{d\theta }{dt}\end{array} \)
- ω = Angular Velocity
- dፀ = Change in angular Position
- dt = Time interval
- SI Unit = Rad/sec
Angular Acceleration
Angular acceleration of the particle P is defined as the rate of change of the angular velocity of the object.
- Mathematically, angular acceleration,
- \(\begin{array}{l}\alpha = \frac{d\omega }{dt}\end{array} \)
- α = Angular Acceleration
- dω = Change in angular Velocity
- dt = Time interval
- SI Unit = Rad/sec2
Kinematics Equation of Rotational Motion
We see that the kinematic quantities in the rotational motion of the object P are angular displacement(Ɵ), the angular velocity(ω), and the angular acceleration(α). These quantities correspond to the displacement(x), velocity(v), and the acceleration(a) respectively in the linear motion.
As we know that the kinematic equations of linear motion are given as:
Where,
- v0 is the initial velocity of the body
- a is the acceleration of the body
- t is the time
- s is the displacement of the body in the given time t
- v is the velocity of the object at time t.
The equations analogous to these for rotational motion can be given as:
Where Ɵ0 is the initial angular displacement, ωo is the initial angular velocity, α is the angular acceleration, ω is the angular velocity at any instant t.
\(\begin{array}{l}\theta -\theta _{0}=(\frac{\omega _{oz}+\omega _{z}}{2})t\end{array} \) |
Where,
- Ɵ0 is the initial angular displacement around the z-axis in radians
- Ɵ is the final angular displacement around the z-axis in radians
- ωoz is the initial angular velocity around the z-axis s-1
- ωz is the final angular velocity around the z-axis s-1
- t is the time in s
To learn more about the kinematics of rotational motion around a fixed axis, download BYJU’S The Learning App.
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Comments