Angular velocity is the rate of change of the angular position of a rotating body. We can define the angular velocity of a particle as the rate at which the particle rotates around a centre point i.e., the time rate of change of its angular displacement relative to the origin. Linear velocity is the measure of “the rate of change of displacement with respect to time when the object moves along a straight path.” Linear velocity is a vector quantity. In this article, let us learn about the relation between linear velocity and angular velocity.
Table of Contents:
Relation Between Linear Velocity and Angular Velocity
Let us consider the randomly shaped body undergoing a rotational motion as shown in the figure below. The linear velocity of the particle is related to the angular velocity. While considering the rotational motion of a rigid body on a fixed axis, the extended body is considered as a system of particles moving in a circle lying on a plane that is perpendicular to the axis, such as the centre of rotation lies on the axis.
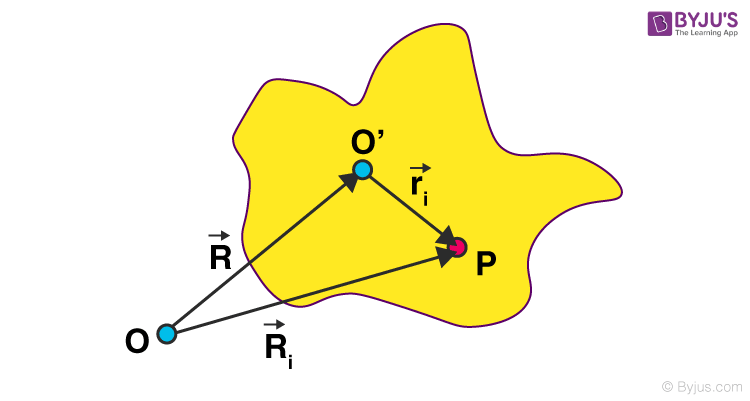
In this figure, particle P has been shown to rotate over a fixed axis passing through O. Here, the particle represents a circle on the axis. The radius of the circle is the perpendicular distance between point P and the axis. The angle indicates the angular displacement Δθ of the given particle at time Δt. The average angular velocity in the time Δt is Δθ/Δt. Since Δt tends to zero, the ratio Δθ/Δt reaches a limit which is known as the instantaneous angular velocity dθ/dt. The instantaneous angular velocity is denoted by ω.
From the knowledge of circular motion, we can say that the magnitude of the linear velocity of a particle travelling in a circle relates to the angular velocity of the particle ω by the relation υ/ω= r, where r denotes the radius. At any instant, the relation v/ r = ω applies to every particle that has a rigid body.
If the perpendicular distance of a particle from a fixed axis is ri, the linear velocity at a given instant v is given by the relation,
Vi = ωri
Similarly, we can write the expression for the linear velocity for n different particles comprising the system. From the expression, we can say that for particles lying on the axis, the tangential velocity is zero as the radius is zero. Also, the angular velocity ω is a vector quantity that is constant for all the particles comprising the motion.
Difference Between Angular Velocity and Linear Velocity
|
Angular Velocity |
Linear Velocity |
| Angular velocity is defined as the rate of change of the angular position of a rotating body. | Linear velocity is defined as the rate of change of displacement with respect to time when the object moves along a straight path. |
| When an object undergoes circular motion, the angular velocity of a particle is along the axis of a circle. Angular velocity remains the same. | When an object undergoes circular motion, the linear velocity of a particle is along the circumference of a circle. Linear velocity varies at every point on the circle. |
| The angular velocity is measured in degrees and radians. | The linear velocity is measured in m/s. |
| Angular velocity is represented by ω. | Linear velocity is represented by v. |
From the video you will learn that angular velocity is not just related to circular motion, instead, circular motion is a special case from which angular velocity is studied.

Frequently Asked Questions – FAQs
What is linear velocity?
State true or false: Linear velocity is a scalar quantity.
What is the SI unit of angular velocity?
Relation between linear velocity and angular velocity is expressed using the which formula?
Vi = ωri
How is linear velocity measured?
Hope you understood in detail about the relation between linear velocity and angular velocity. To learn various science and maths topics, visit BYJU’S.


Comments