Time and Work is one of the most common quantitative aptitude topics which is asked in the Government exams. This is one of those topics which candidates are familiar with even before they start their competitive exam preparation.
The concept of time and work remains the same, however, the type of questions asked may have a bit of variety. Mostly, 1-2 words problems are asked from this topic but candidates must also keep themselves prepared to have questions in data sufficiency and data interpretation to be picked up from time and work.
Candidates can check the detailed syllabus for the quantitative aptitude section along with the list of exams, which include this subject as a part of its syllabus and can visit the linked article.
| Preparing the Quantitative Aptitude questions for the upcoming Government exams? Test your preparation with the links mentioned below: |
For aspirants who shall be appearing for the competitive exams for the first time or the ones who are preparing for the exams for a while must know that sufficient time must be devoted to each subject so that your concept and basics are clear. This will help you cope with the tough competition for each exam.
In this article, we bring to you the concept of time and work along with the formulas which shall help you answer the questions easily. Also, further below in the article, we have a few sample time and work questions with solutions for your reference.
Interested aspirants can also check the links given below and strengthen their preparation for the quantitative aptitude section:
| Data Sufficiency | Data Interpretation | Quadratic Equations |
| Pipes and Cistern | Mixture & Alligation | Problems on Trains |
Time and Work Questions PDF:-Download PDF Here
Time and Work – Introduction and Concept
Before we move on to the questions and important formulas, it is important that a candidate is well aware of the concept and the types of questions which may be asked in the exam.
Time and work deals with the time taken by an individual or a group of individuals to complete a piece of work and the efficiency of the work done by each of them.

Given below are the basic type of questions which may be asked in the exam with respect to the time and work topic:
- To find the efficiency of a person
- To find the time taken by an individual to do a piece of work
- To find the time taken by a group of individuals to complete a piece of work
- Work done by an individual in a certain time duration
- Work done by a group of individuals in a certain time duration
Mostly the questions asked may involve one of these things to find and candidates can use the related formulas to easily get through the answers for the same.
A few other quantitative aptitude related links have been given below. It is suggested that candidates go through each of these topics carefully to excel in the upcoming Government exams:
| Problems on Age | Approximation and Simplification | Number Series |
| Boat and Stream | Shortcut Tricks for Cube, Square and Multiplication | Maths Tricks for Competitive Exams |
Important Time and Work Formula
Knowing the formulas can completely link you to a solution as soon as you read the question. Thus, knowing the formula for any numerical ability topic make the solution and the related calculations simpler.
Given below are a few such important time and work formulas for your reference:
- Work Done = Time Taken × Rate of Work
- Rate of Work = 1 / Time Taken
- Time Taken = 1 / Rate of Work
- If a piece of work is done in x number of days, then the work done in one day = 1/x
- Total Wok Done = Number of Days × Efficiency
- Efficiency and Time are inversely proportional to each other
- X:y is the ratio of the number of men which are required to complete a piece of work, then the ratio of the time taken by them to complete the work will be y:x
- If x number of people can do W1 work, in D1 days, working T1 hours each day and the number of people can do W2 work, in D2 days, working T2 hours each day, then the relation between them will be
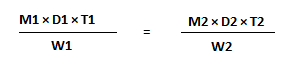
Aspirants for the various Government exams must start their preparation now to ensure they give their 100 per cent and complete hard work and dedication to their preparation.
Time & Work – Sample Questions
All the hard work can go in vain if the candidate does not solve questions based on time and work on a regular basis and try using the different formulas to crack the solution for each question in an even shorter time span.
So, discussed below are a few time and work questions to give an idea as to what type of questions are asked in the competitive exam and what format and pattern is used for the same.
Q 1. A builder appoints three construction workers Akash, Sunil and Rakesh on one of his sites. They take 20, 30 and 60 days respectively to do a piece of work. How many days will it take Akash to complete the entire work if he is assisted by Sunil and Rakesh every third day?
- 10 days
- 15 days
- 25 days
- 30 days
- 45 days
Answer: (2) 15 days
Solution:
Total work done by Akash, Sunil and Rakesh in 1 day = {(1/20) + (1/30) + (1/60)} = 1/10
Work done along by Akash in 2 days = (1/20) × 2 = 1/10
Work Done in 3 days (1 day of all three together + 2 days of Akash’s work) = (1/10) + (1/10) = 1/5
So, work done in 3 days = 1/5
Time taken to complete the work = 5×3 = 15 days
Q 2. To complete a piece of work, Samir takes 6 days and Tanvir takes 8 days alone respectively. Samir and Tanvir took Rs.2400 to do this work. When Amir joined them, the work was done in 3 days. What amount was paid to Amir?
- Rs. 300
- Rs. 400
- Rs. 800
- Rs. 500
- Rs. 100
Answer: (1) Rs.300
Solution:
Total work done by Samir and Tanvir = {(1/6) + (1/8)} = 7/24
Work done by Amir in 1 day = (1/3) – (7/24) = 1/24
Amount distributed between each of them = (1/6) : (1/8) : (1/24) = 4:3:1
Amount paid to Amir = (1/24) × 3 × 2400 = Rs.300
Q 3. Dev completed the school project in 20 days. How many days will Arun take to complete the same work if he is 25% more efficient than Dev?
- 10 days
- 12 days
- 16 days
- 15 days
- 5 days
Answer: (3) 16 days
Solution:
Let the days taken by Arun to complete the work be x
The ratio of time taken by Arun and Dev = 125:100 = 5:4
5:4 :: 20:x
⇒ x = {(4×20) / 5}
⇒ x = 16
Q 4. Time taken by A to finish a piece of work is twice the time taken B and thrice the time taken by C. If all three of them work together, it takes them 2 days to complete the entire work. How much work was done by B alone?
- 2 days
- 6 days
- 3 days
- 5 days
- Cannot be determined
Answer: (2) 6 days
Solution:
Time taken by A = x days
Time taken by B = x/2 days
Time Taken by C = x/3 days
⇒ {(1/x) + (2/x) + (3/x) = 1/2
⇒ 6/x = 1/2
⇒ x = 12
Time taken by B = x/2 = 12/2 = 6 days
Q 5. Sonal and Preeti started working on a project and they can complete the project in 30 days. Sonal worked for 16 days and Preeti completed the remaining work in 44 days. How many days would Preeti have taken to complete the entire project all by herself?
- 20 days
- 25 days
- 55 days
- 46 days
- 60 days
Answer: (5) 60 days
Solution:
Let the work done by Sonal in 1 day be x
Let the work done by Preeti in 1 day be y
Then, x+y = 1/30 ——— (1)
⇒ 16x + 44y = 1 ——— (2)
Solving equation (1) and (2),
x = 1/60
y = 1/60
Thus, Preeti can complete the entire work in 60 days
Time and Work Questions PDF:-Download PDF Here
Candidates must solve more such questions to understand the concept better and analyse the previous year papers to know more about the pattern of questions asked.
Other Related Links:
| Quantitative Aptitude Preparation for Bank Exams | Tips to Prepare Quantitative Aptitude for SBI PO | Quantitative Aptitude Preparation for IBPS PO |
| Bank Exam Syllabus | SSC Syllabus | RRB Syllabus |
Candidates interested in applying for the upcoming Bank, Insurance, SSC, RRB and other Government sector exams must start their preparation now.
For any help and assistance regarding the exam preparation, candidates can turn to BYJU’S.

Comments