The Binary Search algorithm is a fast technique that works efficiently on a sorted list. Thus, it is important to make sure that the list should be a sorted one from which the element is to be searched. Binary search works on the divide and conquer approach, i.e. the list from which the search is to be done is divided into two halves, and then the searched element is compared with the middle element in the array. If the element is found, then the index of the middle element is returned. Otherwise, the search will keep going in either of the halves according to the result generated through the match.
Table of Contents
- Binary Search Pseudocode
- Implementation of Binary Search Algorithm
- Working of Binary Search Algorithm
- Binary Search Complexity
- Advantages of Binary Search Algorithm
- Disadvantages of Binary Search Algorithm
Binary Search Pseudocode
- We have an array to be sorted in ascending order.
- Next, we have two pointer variables, i.e. start and finish.
- The pointer start will be assigned with 0, and the pointer finish will be assigned to the last index of the array.
- Now we have another variable called mid, which indicates the middle of the array, which is calculated as (low+high)/2.
- If the element at the mid index is equal to the searched element, then the mid index will return.
- If the searched element is smaller than the mid index element, then the finish will shift to mid-1, and the whole RHS will be discarded.
- If the searched element is greater than the mid index element, then the start will shift to mid+1, and the whole LHS will be discarded.
Implementation of Binary Search Algorithm
The Binary search algorithm can be implemented in two ways:
- Iterative method
- Recursive method
Iterative approach
binarySearch(array, size)
loop until start is not equal to finish
midIndex = (start + finish)/2
if (element == array[midIndex] )
return midIndex
else if (element > array[midIndex] )
start = midIndex + 1
else
finish = midIndex – 1
Recursive approach
binarySearch(array, element, start, finish)
if start<=finish
midIndex = (start + finish) / 2
if item == array[midIndex]
return midIndex
else if item < array[midIndex]
return binarySearch(array, element, midIndex + 1, finish)
else
return binarySearch(array, element, start, midIndex – 1)
return -1
Working of Binary Search Algorithm
Now, let’s understand the working of the Binary Search Algorithm. Let’s take an example of a sorted array:
Let the elements of the array are –

Let the element to search is, K = 60
Now, we need to find out mid of the array with the formula:
(Start+finish)/2
So, in the given array –
start = 0
finish= 8
mid = (0 + 8)/2 = 4. Thus, 4 is in the middle of the array.


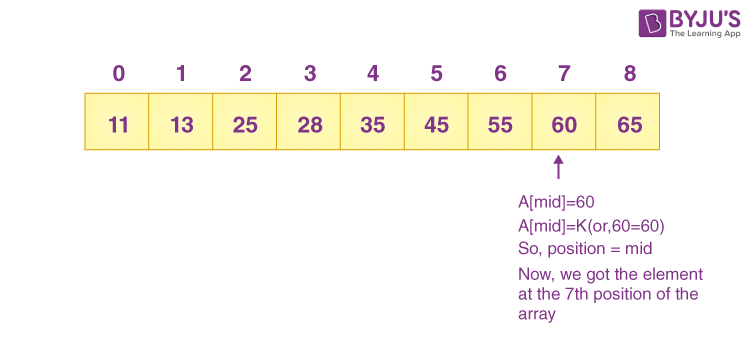
As we have found here the searched element, the index of the matched element will return.
Binary Search Complexity
Now, let’s understand the time and space complexity of Binary Search in the best, average, and worst cases.
- Time Complexity:
- Best case complexity: When the element to be searched is found in the first comparison, i.e. when the searched element is the first middle element, then it is the best case occurrence. Thus, in the binary search, the best case time complexity is O(1).
- Average Case Complexity: In the binary search, the average case of time complexity is O(logn).
- Worst-case complexity: We need to reduce the search space till it has only a single element. Thus, the worst case in time complexity is O(logn)
- Space Complexity:
O(1) is the space complexity in the binary search algorithm.
Advantages of Binary Search Algorithm
- When it comes to comparing large data, it is quite efficient as it works on the technique to eliminate half of the array element.
- It has less compilation time and thus better time complexity.
- As it breaks the array in half, it is considered an improvement over linear search.
Disadvantages of Binary Search Algorithm
- It can only be implemented over a sorted array.
- The process of sorting and searching in an unsorted array will take time. Thus, binary search is not a good option in such cases.
Keep learning and stay tuned to get the latest updates on GATE Exam along with GATE Eligibility Criteria, GATE 2023, GATE Admit Card, GATE Syllabus for CSE (Computer Science Engineering), GATE CSE Notes, GATE CSE Question Paper, and more.
Also Explore,
Comments