The earth and the moon are attracted to each other by gravitational force. The earth attracts the moon with a force that is:

Same as that exerted by the moon

More than that exerted by the moon

Less than that exerted by the moon

Not related to that exerted by the moon

Law of gravitation gives the gravitational force between

any two bodies having some mass

the Earth and a point mass only

Gravitation - Newton’s Law of Gravitation, Gravitational Force, Solved Examples

Gravitation or gravity is the force of attraction between any two bodies. All the objects in the universe attract each other with a certain amount of force, but in most cases, the force is too weak to be observed due to the very large distance of separation. Besides, gravity’s range is infinite, but the effect becomes weaker as objects move away.

Download Complete Chapter Notes of Gravitation
Download Now

This force of attraction was first observed by Sir Isaac Newton and was presented as Newton’s law of gravitation in the year 1680. However, gravitation can generally exist in two main instances.

1. Gravitation may be the attraction of objects by the earth

For example,

If a body (ball) is thrown upwards, it reaches a certain height and falls downwards because of the gravity of the earth.

2. Gravitation may be the attraction of objects in outer space.

For example,

The force of attraction between the other planets and the sun.

Gravitational Force
History
Newton’s Law of Gravitation
Vector Form
Formula
Derivation from Kepler’s Law
FAQs

What Is Gravitational Force?

Each body in this universe attracts other bodies towards itself with a force known as Gravitational Force. Thus, gravitation is a study of the interaction between two masses. Out of the two masses, the heavier one is called source mass, and the lighter one is called test mass.

Gravitational force is a central force which depends only on the position of the test mass from the source mass and always acts along the line joining the centres of the two masses.

\(\begin{array}{l}\vec{F}(r) = f(r)\hat{r}\end{array} \)

The core problem of gravitation has always been in understanding the interaction between the two masses and their relativistic effects.

⇒ Also, Check: Gravitational field intensity

History of Gravitational Theory

Ptolemy proposed the geocentric model, which failed to understand planetary motions, and led to the development of the heliocentric model by Nicholas Copernicus. His idea is based on the rotation of a test mass around the source mass in circular orbits; although the model correctly predicts the position of planets and their motions but has failed to explain many aspects, like the occurrence of seasons, which led to the construction of a model based on Kepler’s laws of planetary motion.

Newton’s Law of Gravitation

According to Newton’s law of gravitation, every particle in the universe attracts every other particle with a force whose magnitude is,

Directly proportional to the product of their masses, i.e., F ∝ (M₁M₂) . . . . (1)
Inversely proportional to the square of the distance between their centre, i.e., (F ∝ 1/r²) . . . . (2)

On combining equations (1) and (2), we get,

F ∝ M₁M₂/r²

F = G × [M₁M₂]/r² . . . . (7)

Or, f(r) = GM₁M₂/r²[f(r) is a variable, non-contact, and conservative force]

As f(r) varies inversely as a square of ‘r,’ it is also known as the inverse square law force. The proportionality constant (G) in the above equation is known as the gravitational constant.

The dimension formula of G is [M^-1L³T^-2]. Also, the value of the gravitational constant,

In SI units: 6.67 × 10^-11 Nm²kg^-2,
In CGS units: 6.67×10^-8 dyne cm²g^-2

Vector Form of Newton’s Law of Gravitation

The vector form of Newton’s law of gravitation signifies that the gravitational forces acting between the two particles form action-reaction pair.

Derivation of Newton's Law of Gravitation

From the above figure, it can be seen that the two particles of masses are placed at a distance.

\(\begin{array}{l}\vec{r_{21}}=(\vec{r_{2}}-\vec{r_{1}})\end{array} \)

The direction of the vector is from M₁ to M₂

Therefore, the force applied on M₂ by M₁ is

\(\begin{array}{l}\vec{F_{21}}=-\frac{GM_{1}M_{2}}{r^{2}_{21}}\hat{{r_{21}}}\end{array} \)

The negative sign indicates the attractive nature of the force.

Similarly, force on M₁ and M₂

\(\begin{array}{l}\vec{F_{12}}=-\frac{GM_{1}M_{2}}{r^{2}_{12}}\hat{{r_{12}}}\end{array} \)

Since,

\(\begin{array}{l}\hat{r_{12}}= -\hat{r_{21}}\end{array} \)

\(\begin{array}{l}\vec{F_{12}}=-\frac{GM_{1}M_{2}}{(-r_{21})^{2}}[\hat{-{r_{21}}}]\end{array} \)

\(\begin{array}{l}\vec{F_{12}}=\frac{GM_{1}M_{2}}{(r_{21})^{2}}[\hat{{r_{21}}}]\end{array} \)

\(\begin{array}{l}=-\vec{F_{21}}\end{array} \)

Hence, the applied forces are equal and opposite. Also, the gravitational force follows Newton’s third law.

Gravitational Force Formula

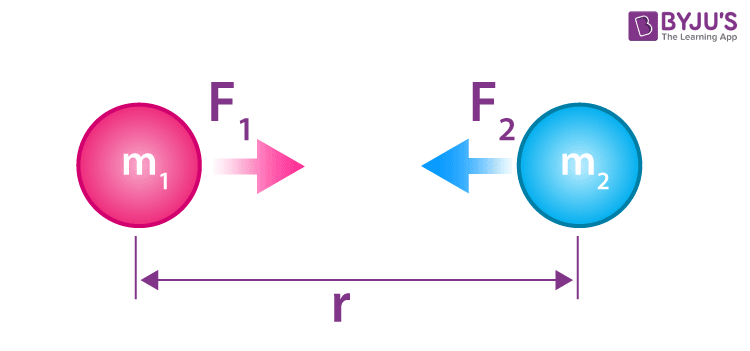
Gravitational force is explained using Newton’s law of gravitation. Gravitational force decides how much we weigh and how far a ball travels when thrown before it lands on the ground.

Also Read: Important Gravitation Formulas for JEE

According to Newton’s law of gravitation, every particle in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Mathematically, it can be represented as,

F = Gm₁m₂/r²Where,

F is the gravitational force between two objects measured in Newton (N).
G is the universal gravitational constant with a value of 6.674 × 10^-11 Nm²kg^-2.
m₁is the mass of one massive body measured in kg.
m₂ is the mass of another massive body measured in kg.
r is the separation between them measured in kilometre (Km).

Principle of Superposition of Gravitational Forces

Newton’s law of gravitation answers only the interaction between two particles; if the system contains ‘n’ particles, there are n(n – 1)/2 such interactions.

According to the principle of superposition, if each of these interactions acts independently and uninfluenced by the other bodies, the results can be expressed as the vector summation of these interactions:

F = F₁₂+ F₁₃+ F_{14 . . . . . .}+ F_1n.

It states that:

“The resultant gravitational force F acting on a particle due to the number of point masses is equal to the vector sum of forces exerted by the individual masses on the given particle”.

Derivation of Newton’s law of Gravitation from Kepler’s Law

Suppose a test mass is revolving around a source mass in a nearly circular orbit of radius ‘r’ with a constant angular speed (ω). Then, the centripetal force acting on the test mass for its circular motion is,

F = mrω² = mr × (2π/T)²

According to Kepler’s 3rd law, T² ∝ r³

Using this in force equation, we get,

F = 4π²mr/Kr³ [Where, K = 4π²/GM]

⇒ F = GMm/r², which is the equation of Newton’s law of gravitation.

Solved Examples

1. What is the force of gravity acting on an object of mass 2000 kg at the Earth’s surface?

Given:

Mass of Earth (m₁) = 5.98 × 10²⁴kg

Mass of object (m₂) = 2000kg

The radius of the Earth (r)= 6.38 × 10⁶m

Acceleration due to gravity (g) = 9.8 m/s²

Universal constant (G) = 6.67 x 10^-11 N m² / kg²

Solution:

F = Gm₁m₂/r²

F = ( 6.67 x 10^-11) (5.98 × 10²⁴)(2 x 10³)/(6.38 × 10⁶)²

F = (7.978 x 10¹⁷)/ (4.07044 × 10¹³)

F = 1.959 x 10⁴or F = 19.59 N

2. What is the force of gravity acting on an object of mass 1000 kg at 20,000 meters above the Earth’s surface?

Given:

Mass of Earth (m₁) = 5.98 × 10²⁴kg

Mass of object (m₂) = 1000kg

The radius of the Earth (r)= 6.38 × 10⁶m

Acceleration due to gravity (g) = 9.8 m/s²

Universal constant (G) = 6.67 x 10^-11 N m² / kg²

h = 2 x 10⁴ m

Solution:

F = Gm₁m₂/(r +h)²

F = ( 6.67 x 10^-11) (5.98 × 10²⁴)(1 x 10³)/(6.38 × 10⁶ + 2 x 10⁴ )²

F = (3.988 x 10¹⁷)/(4.058 x 10¹³)

F = 9,827.50

F = 0.9827 x 10⁴

Related Links

Acceleration due to gravity

Gravitational potential energy

Read More:

Gravitation Rapid Revision for JEE

What Is Gravitation? – Video Lesson

Gravitation – Top 10 Most Important and Expected JEE Questions

Frequently Asked Questions on Gravitation

Will your weight be constant when you are travelling to Greenland from Brazil?

No, it will increase. As the acceleration due to gravity is greater at the poles and lesser at the equator, because of the bulged oblate shape of the earth, we will feel heavier at Greenland. (Greenland is closer to the North Pole, and Brazil is closer to the equator).

Can you screen the effect of gravitation by any material medium?

No, the gravitational effect cannot be screened, unlike electrostatic force, because the gravitational force does not depend on any medium.

Why are space rockets launched eastward?

The Earth spins (rotates) from west to east in 24 hours. If the space rockets are launched in the same direction, the relative velocity of the rocket increases, which helps it to rise without much fuel.

Why does a bouncing ball bounce higher on hills than on planes?

As the altitude increases, the acceleration due to gravity decreases. Therefore, the ball bounces higher in hills than on planes.

The gravitational potential energy is negative. Why?

The reference point of zero potential energy is at infinity, and the gravitational force is always attractive. Therefore, the gravitational potential energy, which is the negative of work done, is always negative.

Why is Newton’s law of gravitation called universal law?

Newton’s law of gravitation holds good irrespective of the nature of the interacting bodies at all places and at all times.

What is the weight of the body at the centre of the Earth?

The weight of the body at the centre of the earth is zero.
W = mg = 0
(g at the centre of the earth is zero).

Does friction arise due to gravitation?

Friction does not arise due to gravitation. Its origin is electrical in nature.

Gravitation - Gravitational Force and Newton's Law of Gravitation

Table of Contents