Sir Isaac Newton put forward the universal law of gravitation in 1687 and used it to explain the observed motions of the planets and moons. In this article, let us familiarize ourselves with Newton’s Law of Universal Gravitation.
|
Table of Contents |
What is the Universal Law of Gravitation?
Newton’s Law of Universal Gravitation states that every particle attracts every other particle in the universe with force directly proportional to the product of the masses and inversely proportional to the square of the distance between them.
The universal gravitation equation thus takes the form
\(\begin{array}{l}F\propto \frac{m_{1}m_{2}}{r^2}\end{array} \)
\(\begin{array}{l}\Rightarrow F=G\frac{m_{1}m_{2}}{r^2}\end{array} \) |
Universal Gravitation Equation
Newton’s conclusion about the magnitude of gravitational force is summarized symbolically as
\(\begin{array}{l}F= G\frac{m_{1}m_{2}}{r^2}\end{array} \)
where, F is the gravitational force between bodies, m1 and m2 are the masses of the bodies, r is the distance between the centres of two bodies, G is the universal gravitational constant.
The constant proportionality (G) in the above equation is known as the universal gravitation constant. Henry Cavendish experimentally determined the precise value of G. The value of G is found to be G = 6.673 x 10-11 N m2/kg2.
The Universal Gravitational Law can explain almost anything, right from how an apple falls from a tree to why the moon revolves around the earth. Watch the video and understand the beauty of the law of universal gravitation.
Gravitational Constant
The value of the gravitational constant is extremely difficult to measure accurately. Henry Cavendish devised a clever apparatus for measuring the gravitational constant.
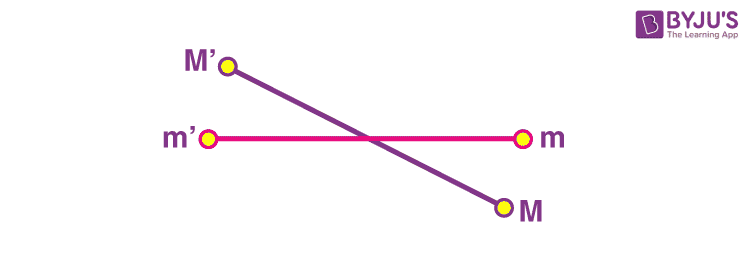
As shown in the figure, the masses m and m’ are attached to either end of the beam. The beam is attached to strong support with the help of a string. The string is tied to the middle of the beam, allowing it to reach an equilibrium. Now, two large masses M’ and M, are lowered next to them. The gravitational force between the two pairs of masses causes the string to twist such that the amount of twisting is just balanced by the gravitational force. The gravitational force can be measured by appropriate calibration. Since we know the value of masses and distances between them, the only unknown quantity is G in the universal law of gravitation. Thus, the value of G is calculated from the measured quantities.
Universal Gravitation Solved Example
Calculate the gravitational force of attraction between the Earth and a 70 kg man standing at a sea level, a distance of 6.38 x 106 m from the earth’s centre.
Solution:
Given:
m1 is the mass of the Earth which is equal to 5.98 x 1024 kg
m2 is the mass of the man which is equal to 70 kg
d = 6.38 x 106 m
The value of G = 6.673 x 10-11 N m2/kg2
Now substituting the values in the Gravitational force formula, we get
Weight and the Gravitational Force
In Newton’s law of gravity, we noticed that mass is a crucial quantity. We consider mass and weight to be the same, but they are different in reality. Weight is the gravitational force exerted on an object of a certain mass. The object’s weight can be obtained by multiplying the object’s mass m by the acceleration due to gravity g, at the Earth’s surface. The measured gravitational acceleration at the Earth’s surface is found to be about 980 cm/second/second.
The measure of how much material is in an object is known as mass, while weight is the measure of the gravitational force exerted on the material in a gravitational field; thus, mass and weight are proportional to each other acceleration due to gravity as the proportionality constant. Therefore, it is observed that the mass is constant for a given object, but the weight depends on the object’s location. To better understand, let us consider the following example, say we transported an object of mass m to the surface of Neptune, the gravitational acceleration would change because the radius and mass of the Neptune both differ from those of the Earth. Thus, our object has mass m both on the surface of the Earth and on the surface of the Neptune, but it will weigh much more on the surface of Neptune because the gravitational acceleration there is 11.15 m/s2.
Universality of Gravity
Gravitation interactions not only exist between the earth and other objects, but it also exists between all objects with an intensity that is directly proportional to the product of their masses. The law of universal gravitation helps scientists study planetary orbits. The small perturbations in a planet’s elliptical motion can be easily explained owing to the fact that all objects exert gravitational influences on each other.
Watch the video and learn more about the reason behind the falling of objects
Why doesn’t the moon crash into the earth?
The forces of speed and gravity are what keeps the moon in constant orbit around the earth. The Moon seems to hover around in the sky, unaffected by gravity. However, the reason the Moon stays in orbit is precise because of gravity. In this video, clearly, understand why the moon doesn’t fall into the earth.
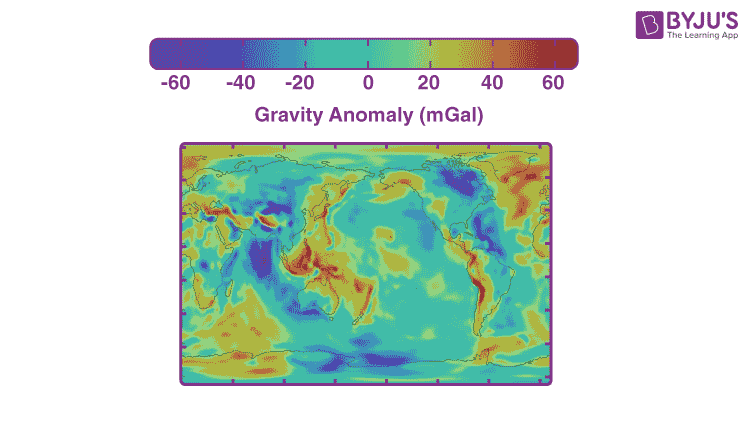
Is the force of Gravity the same all over the Earth?
Gravity isn’t the same everywhere on earth. Gravity is slightly stronger over the places with more underground mass than places with less mass. NASA uses two spacecraft to measure the variation in the Earth’s gravity. These spacecraft are a part of the Gravity Recovery and Climate Experiment (GRACE) mission.
Watch the video and solve complete NCERT exercise questions in the chapter Gravitation
Frequently Asked Questions – FAQs
What is Newton’s universal law of gravitation?
Newton’s Law of Universal Gravitation states that every particle attracts every other particle in the universe with force directly proportional to the product of the masses and inversely proportional to the square of the distance between them.
Is there gravity in space?
Gravity is everywhere. It gives shape to the orbits of the planets, the solar system, and even galaxies. Gravity from the Sun reaches throughout the solar system and beyond, keeping the planets in their orbits. Gravity from Earth keeps the Moon and human-made satellites in orbit.
What is the value of Gravitational Constant G on the moon?
The acceleration due to gravity on the surface of the moon is 1.625 m/s2.
Is the value of g the same everywhere on Earth?
No, the value of g is different at different places on the surface of the earth. The acceleration due to gravity is smaller at the equator than at the poles. This is because g is inversely proportional to the radius and the radius of the earth is smaller at poles and larger at the equator.
How is Einstein’s theory of gravity different from Newton’s?
According to Einstein, objects move toward one another because of the curves in space-time, not because of the force of attraction between them.
Who put forward the universal law of gravitation?
In 1687, Sir Isaac Newton put forward the universal law of gravitation.
Give the universal gravitational equation.
The universal gravitational equation is given by:
What is the value of ‘G’?
The value of G is 6.673 x 10-11 N m2/kg2.
What is gravitational force?
The universal force of attraction acting between objects is known as the gravitational force.
Give one example for gravitational force.
The force acting between the Sun and the Earth is one example of gravitational force.
The full summary of the chapter Gravitation Class 9 |
Important questions in the chapter Gravitation Class 9 |
Stay tuned to BYJU’S and Fall in Love with Learning!
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Comments