The power of a Lens is one of the most interesting concepts in ray optics. The detailed concept of this topic is given in the below article so that learners can understand this chapter more effectively.
| Table of Contents |
What Is Power of a Lens?
Simply put, the power of a lens in Ray Optics is its ability to bend light. The greater the power of a lens, the greater its ability to refract light that passes through it. For a convex lens, the converging ability is defined by power and in a concave lens, the diverging ability.
Do you notice the connection between the focal length and the bending of the light ray? As the focal length decreases, the amount the light bends increases. Therefore, we can conclude that the power of a lens is inversely proportional to the focal length of the lens. A short focal length basically contributes to high optical power.
Power of a Lens Formula
To find the power of a lens in Ray Optics, the following formula can be used.
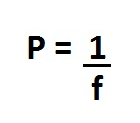
If the focal length is given in metres (m), the power of the lens is measured in Diopters (D), as in the unit of power of the lens is diopter. Another thing you should keep in mind is that for a converging lens the optical power is positive and for a diverging lens, it is negative.
For example, if the focal length of a lens is 20 cm, converting this to metres, we get 0.2 m. To find the power of this lens, take the reciprocal of 0.2, and we get 5. Therefore, the power of this particular lens is 5 D.
If you’ve previously read about the lens maker’s formula, you would’ve realised that what we are calculating there is actually the power of the lens. This means that you can calculate the power of a lens using radii of curvature of two surfaces and the refractive index of the lens material.
An important application of using the power of lenses is in ‘Optometry”. Optometrists prescribe corrective lenses (either convex or concave lens) based on depreciating vision. Your eye is basically a lens and you may experience problems with having a clear vision sometimes. This can be rectified by wearing corrective lenses with the appropriate power.
Optics Formulas
Following are the list of other optic formulas that are studied in optics:
| Total internal refraction | \(\begin{array}{l}\frac{n_{1}}{n_{2}}=\frac{sin r}{sin i}\end{array} \) |
| Critical angle, Ө | \(\begin{array}{l}sin \Theta =\frac{n_{2}}{n_{1}}\end{array} \) |
| Prism formula | \(\begin{array}{l}\mu =\frac{sin\frac{A+\delta _{m}}{2}}{sin\frac{A}{2}}\end{array} \) |
| Lens maker’s formula | \(\begin{array}{l}\frac{1}{f}=(\mu -1)(\frac{1}{R_{1}}-\frac{1}{R_{2}})\end{array} \) |
The video about the fundamentals of spherical lenses
Frequently Asked Questions – FAQs
What is meant by the power of a lens?
What is the relationship between the focal length and the power of a lens?
What is the SI unit for the power of a lens?
State TRUE or FALSE: Power of a converging lens is positive.
Write the lens maker’s formula?
where,
f is the focal length (half the radius of curvature)
n is the refractive index of the material used
R1 is the radius of curvature of sphere 1
R2 is the radius of curvature of sphere 2
Watch the video and solve the previous year questions in the chapter Light Reflection and Refraction Class 10
Was this article interesting? Check out other related articles by visiting BYJU’S.
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
very nice explanation