Gravitational Force

Gravitational Force Formula

Where,

• F is the gravitational force between two bodies
• m₁ is the mass of the first body
• m₂ is the mass of the second body
• r is the distance between the centres of two bodies

The force exerted by two bodies with mass m₁ and m₂, whose centres are r units apart are given as:

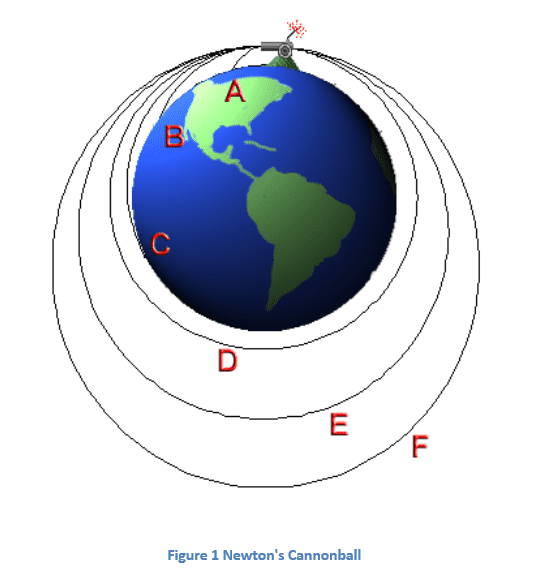
Newton’s cannonball is a ‘thought experiment’ given by Newton, which leads to the hypothesis that the force of gravity is universal, and it plays a major role in planetary motion.

According to this thought experiment, he assumed a cannon on the top of a very high mountain peak. The following cases can arise if the cannon is loaded with gunpowder and fired.

• If the speed of the cannon is low, it falls on the Earth following a projectile motion.
• If at that particular altitude, the speed of the cannon is equal to the orbital speed, the cannonball will go on circling the Earth about a fixed orbit.
• If the speed of the cannonball is higher than the orbital velocity but is insufficient to leave the Earth, i.e. less than the escape velocity of the Earth then, the cannonball continues to revolve around Earth in an elliptical orbit.
• If the speed is equal to escape velocity or greater than that, the cannonball leaves the Earth in a parabolic or hyperbolic trajectory.

Now, coming back to our original question, how do planets revolve around the Sun? Well, the gravity of the Sun keeps the planets around it in fixed orbits. Due to the same reason, the Moon orbits the Earth due to the gravitational pull of the Earth on the Moon. But if the Sun is attracting the Earth, why doesn’t it fall into it or why doesn’t the Moon collide with the Earth?

The reason behind this is that Earth has a velocity perpendicular to the gravitational force exerted by the Sun. Thus, the planets move sideways in addition to getting attracted by the Sun, which keeps them moving in specified orbits. Similarly, the Moon revolves around the Earth without falling into it.

The below video helps to visualise the concept of the gravitational field

Related Articles:

• Gravity
• Gravitational Constant and Universal Law Of Gravitation
• Kepler’s Laws of Planetary Motion

Examples Of Gravity

As we learned in this article that gravity is the force that pulls two bodies together, below are the examples of gravity:

• The force acting between the Sun and the Earth.
• The force that is responsible for the revolution of the Moon around the Earth.
• The tides that are caused in the ocean are due to the force from the Moon.
• The force that is holding all the gases in the Sun.
• The force that acts on us makes us walk on the ground and not float in the air.

Solved Problems on Gravitational Force 

Q1) Calculate the force of gravity acting on a body at the Earth’s surface. Consider the following values:

• • Let the mass of the body be 1000 kg
  • Consider the Earth’s mass to be 5.98 x 10²⁴ kg
  • The radius of the Earth as 6.38 x 10⁶ m
  • Universal constant G = 6.67 x 10^–11

Solution:

Let us consider the mass of the Earth as m₁ and the mass of the body as m₂.

We know that the force of gravity is given by the formula

\(\begin{array}{l}F=G\frac{m_{1}m_{2}}{r^2}\end{array} \)

Substituting the values in the above equation, we get

\(\begin{array}{l}F=6.67\times 10^{-11}\frac{5.98\times10^{24}\times10^3}{({6.38\times10^{6})}^2}\end{array} \)

Solving,

\(\begin{array}{l}F=\frac{39.8\times10^{16}}{40.7\times10^{12}}=0.9778\times10^4\, or\,9.778\,N\end{array} \)

The force of gravity acting on the body at the Earth’s surface is 9.778 N.

Q2) Calculate the force of gravity acting on a body 10,000 metres above the Earth’s surface.

Consider the object’s mass to be 1000 kg.

Solution:

Let us consider the following:

The radius of the Earth as 6.38 × 10⁶ m

The mass of the Earth as 5.98 x 10²⁴ kg

The universal constant as 6.67×10^–11

The force of gravity acting on the body can be calculated using the formula

\(\begin{array}{l}F=G\frac{m_{1}m_{2}}{{(r+h)}^2}\end{array} \)

Substituting the values in the above equation, we get

The force of gravity acting on the body 10,000 metres above the Earth’s surface is 9.755 N.
See the video below, to have a clear idea of how gravity works.

Frequently Asked Questions – FAQs

Q1

What is gravitational force?

The universal force of attraction, which is acting between objects, is known as the gravitational force.

Q2

State the universal law of gravitation

The universal law of gravitation states that “The force of attraction between any two bodies is directly proportional to the product of their masses and is inversely proportional to the square of the distance between them”.

Q3

Give the formula to find the gravitational force?

The formula to find the gravitational force is:

\(\begin{array}{l}F\propto \frac{(m_{1}m_{2})}{r^{2}}\end{array} \)

Where,

F is the gravitational force between two bodies

m₁ is the mass of the first body

m₂ is the mass of the second body

r is the distance between the centres of two bodies

Q4

State true or false: The force of gravity exists between the Sun and the Earth.

True.

Q5

Give some examples to prove the presence of gravitational force.

The tides caused in the ocean are due to the force from the Moon.

The force that is holding all the gases in the Sun.

The force which helps to walk on the ground.

The full summary of the chapter Gravitation Class 9

The important questions in the chapter Gravitation Class 9

Hope you have learned in detail the gravitational force. Stay tuned with BYJU’S to know more about various science and math concepts.