Heat is a form of energy that produces the sensation of hotness. Thermodynamics is the branch of Physics that deals with the energy relationships involving heat, mechanical energy and other forms of energy. The entire formulation of thermodynamics is based on a few fundamental laws which have been established on the basis of the human experience of the experimental behaviour of macroscopic aggregates of matter collected over a long period of time.
Table of Contents
- Gas Laws
- Methods of Heat Transfer
- Basic Terminology in Thermodynamics
- Thermodynamic Equilibrium
- Internal Energy
- Zeroth Law of Thermodynamics
- Modes of Energy Transfer
- First Law of Thermodynamics
- Specific Heat Capacity
- Latent Heat
- Newton’s Law of Cooling
- Degrees of Freedom
- Second Law of Thermodynamics
- Heat Engine
- Enthalpy
- Entropy
- Clausius Clapeyron Equation
- Carnot Engine
- Refrigerator
- Gibbs Free Energy
- Third Law of Thermodynamics
- Solved Examples
- Practice Problems
- Frequently Asked Questions
Gas Laws
Like solids and liquids, gases also expand on heating. The volume of expansion of the gas depends not only on the temperature but also on the pressure to which it is subjected. Thus, there are three variables for gases: volume, pressure and temperature. To study the variation of any two variables, the third is kept constant. The interrelationships between these variables are known as gas laws.
Boyle’s Law
The pressure is inversely proportional to the volume at a constant temperature.
P ∝ 1/V
PV = constant
Charles’s Law
The volume of the gas is directly proportional to the absolute temperature at constant pressure.
Gay-Lussac’s Law
The pressure of the gas is directly proportional to the absolute temperature at constant volume.
Perfect Gas Equation
It is the relation connecting the pressure, volume and temperature of the given mass of gas. It is obtained from Boyle’s law and Charle’s law which are obeyed by a perfect gas. If one mole of gas is considered, then
PV = RT
Here, P is the pressure
V is the volume
R is the universal gas constant
T is the absolute temperature
Methods of Heat Transfer
Conduction: Conduction is the transfer of heat from the hotter part of the body to the colder part of the body without the actual movement of the particles in between.
Convection: The transmission of heat due to the actual movement of the medium is called convection.
Radiation: Radiation is the process by which heat gets transmitted from one point to another without the action of any material in between.
Basic Terminology in Thermodynamics
| Thermodynamic System | A certain amount of matter is enclosed by a real or imaginary boundary. A system is said to be closed if it can exchange energy but not matter. A system is said to be open if it can exchange both energy and matter |
| Surrounding | The part of the universe other than the system which will interact with it |
| Boundary | The actual or imaginary surface that separates the system and the surrounding |
| Thermodynamic Coordinates | Measurable quantities such as pressure, volume and temperature |
| Thermodynamic State | The condition in which the system exists |
| Equation of State | It is the mathematical equation that relates the thermodynamic coordinates of the given system. For example, PV = RT |
| Extensive Properties | The properties of a system that depend only on the mass of the system. For example, volume, pressure, temperature, entropy, etc |
| Intensive Properties | Properties of the system that do not depend on the mass of the system. For example, temperature, pressure, density, etc. |
| Thermodynamic Process | The process in which there is a change in the thermodynamic coordinates |
| Isothermal Process | The process that takes place at a constant temperature |
| Adiabatic Process | The process in which the heat neither enters the system nor leaves the system |
| Isobaric Process | The process that takes place at a constant pressure |
| Isochoric Process | The process that takes place at a constant volume |
| Reversible Process | A reversible process is a process that can be retraced in the opposite direction so that the system and the surroundings pass through exactly the same state at each stage as in the direct process |
| Irreversible Process | A process that cannot be retraced in the reverse order by reversing the controlling factors |
| Cyclic Process | In this process, the system comes back to its initial state after undergoing a series of changes |
| Quasistatic Process | Very slow process, and the system is always in thermal equilibrium |
Thermodynamic Equilibrium
A system that is in thermal, mechanical and chemical equilibrium is called the thermodynamic equilibrium.
Thermal equilibrium: A thermodynamic system is said to be in thermal equilibrium if the temperature of every part of the system is the same as that of the surroundings.
Mechanical equilibrium: A thermodynamic system is said to be in mechanical equilibrium if there is no unbalanced force on the part of the system or the whole system.
Chemical equilibrium: A system is said to be in chemical equilibrium when its chemical composition is the same throughout the system.
Internal Energy
Internal energy is the sum total of the kinetic energy and potential energy of the atoms/molecules due to internal factors. The energy possessed by the atoms or molecules by virtue of their motion is called kinetic energy.
Zeroth Law of Thermodynamics
The law states that “Two systems in thermal equilibrium with a third system are also in thermal equilibrium with each other”.
Modes of Energy Transfer
There are two methods to change the internal energy of the system, i.e., heat and work.
Heat
Heat is the energy transferred due to the temperature difference between the system and the surrounding area. On heating, the kinetic energy of the molecules increases and therefore, the internal energy increases.
Work
Work is the energy spent to overcome an external force. When the system does work against external pressure, it tends to reduce the internal energy, and on the other hand, when the system contracts due to external pressure, it tends to increase the internal energy.
Thermal Conductivity
The ability of a conductor to conduct heat is called thermal conductivity. It is defined as the quantity of heat flowing per second through the unit area of the block of unit thickness when the temperature difference between the two faces is 1K.
First Law of Thermodynamics
If some quantity of heat is supplied to a system capable of doing external work, then the quantity of heat absorbed by the system is equal to the sum of the increase in the internal energy of the system and the external work done by the system.
dQ = dU + dW
Here, dQ is the amount of heat given to the system
dU is the increase in the internal energy
dW is the external energy done by the system
Applications of the First Law of Thermodynamics
1. Isothermal Process
2. Adiabatic Process
3. Isobaric Process
4. Isochoric Process
Work done in an Isothermal Process
Work done by an ideal gas, when it expands from volume V1 to volume V2 isothermally at temperature T, is given by
W = RTloge(V2/V1) (for one mole of the gas)
Also W = RTloge(P2/P1) (Since P1V1 = P2V2)
Examples of isothermal processes:
- Melting
- Boiling
Work done in an Adiabatic Process
Work done by an ideal gas in an adiabatic process is given by
T1 and T2 are the temperatures in the initial and final states of gas.
Examples of the adiabatic process:
- Propagation of sound waves in a gas
- Bursting of an automobile tube inflated with air
Work done in an Isobaric Process
Work done in an isobaric process is given by W = P(V2 – V1)
The heating of water or any liquid at atmospheric pressure is an example of an isobaric process.
Work done in an Isochoric Process
Work done in an isochoric process, W = 0
The process of melting in which a solid is converted into a liquid is nearly isochoric, as the change in the volume due to melting is negligible.
Heat Added or Removed
(a) For an isothermal process
Q = nRTloge (V2/V1)
(b) For adiabatic process
Q = 0
(c) For isobaric process
Q = nCp△T
(d) For isochoric process
Q = nCv△T
Limitations of the First Law of Thermodynamics
1. The first law of thermodynamics does not indicate the direction in which the change can proceed.
2. The law does not indicate the extent to which the change can take place.
Specific Heat Capacity
The specific heat capacity of a substance can be defined as the amount of heat required to raise the temperature of the unit mass of the substance through 10C.
(a) Specific heat capacity at constant volume: The specific heat capacity at constant volume is the amount of heat required to raise the temperature of 1 g of the gas through 10C, keeping the volume of the gas constant.
(b) Specific heat capacity at constant pressure: The specific heat capacity at constant pressure is the heat required to increase the temperature of 1 g of substance through 10C, keeping the pressure constant.
Mayer’s Formula
Mayer’s formula is given by the difference between the specific heat of a gas at constant pressure and specific heat capacity at constant volume. Mayer’s formula is expressed as,
Cp – Cv = R
Here, Cp is the specific heat capacity at constant pressure.
Cv is the specific heat capacity at constant volume.
R is the universal gas constant.
Mayer’s relation is valid only for perfect gases.
Latent Heat
Latent heat is the amount of heat required to change the state of the unit mass of the substance at constant pressure and temperature.
L = ΔQ/m
Latent heat of fusion: It is the amount of heat required to change the state from solid to liquid.
Latent heat of vaporisation: It is the heat required to change the state from liquid to gas.
Newton’s Law of Cooling
The rate of loss of heat by a body is directly proportional to the temperature difference between the body and the surroundings, provided the difference is small.
Degrees of Freedom
The total number of independent variables which are necessary to specify the position of the object is called the degrees of freedom.
Law of Equipartition of Energy
The law of equipartition of energy states that the total energy is equally shared by all the degrees of freedom, and the average energy of a molecule in a gas associated with each degree of freedom is (½) kT, where
k is the Boltzmann constant, and T is its absolute temperature.
Ratio of specific heats
The ratio of the specific heat capacity of a gas at constant pressure to that at constant volume (Cp/Cv) is an important constant.
It has a value between 1 and 1.67
The knowledge of
Second Law of Thermodynamics
Kelvin-Planck’s Statement
It is impossible to derive a continuous supply of work by cooling a body to a temperature lower than that of the coolest of its surroundings.
Clausius Statement
It is impossible to make heat flow from a body at a lower temperature to a body at a higher temperature without doing any external work on the working substance.
Heat Engine
A heat engine is a machine that converts heat energy to mechanical energy. The heat engine has three parts, the hot body, called the source, the working substance and the cold body, called the sink. The working substance is taken through a cyclic process. During the process, the working substance will absorb the heat from the source at a higher temperature and perform some work, then reject the heat to the sink at a lower temperature.

Efficiency of the Heat Engine
The thermal efficiency of the heat engine is the ratio of the heat that gets converted into work to the total heat absorbed from the source during a complete cycle. The working substance absorbs a certain amount of heat Q1 during isothermal expansion. It rejects an amount of heat Q2 into the sink during the isothermal compression.
Efficiency, η = Work done/Heat supplied
= (Q1 – Q2)/Q1
= 1 – Q2/Q1
Q2/Q1 = T2/T1
η = 1 – T2/T1
The efficiency of the Carnot’s engine depends only on the temperature of the source and sink. It does not depend on the working substance.
Enthalpy
Chemical reactions are generally carried out at constant pressure (atmospheric pressure), so it has been found useful to define the new state function Enthalpy. Enthalpy is given by the sum of the internal energy and the product of the pressure and volume of a thermodynamic system. It is measured in joules or ergs since it has the dimension of energy.
H = U + PV
Here,
H is the enthalpy
U is the internal energy
P is the pressure
V is the volume
Factors Affecting the Enthalpy of a Reaction
a) Temperature
b) Physical states of reactants and products
c) Allotropic forms of elements
d) Pressure and volume
Entropy
The thermal energy per unit temperature that is not available for doing useful work is called entropy. The ordered motion of molecules will result in useful work. So, the amount of molecular disorder or randomness of the system is called entropy.
Important Facts about Entropy
a) Entropy of the universe increases in all-natural processes
b) Change in the entropy depends only on the initial and final states of the system
c) Entropy is not conserved
d) Entropy can be created but not destroyed
Clausius Clapeyron Equation
It relates the rate of change of pressure with temperature to latent heat. It can be applied to any equilibrium between two phases, namely solid and liquid, liquid and water etc. According to the Clausius Clapeyron equation,
Here, L is the latent heat
V1 is the volume of the first state
V2 is the volume in the final state into which the substance changes
Latent heat is the quantity of heat supplied to the unit mass of the substance during the change of state.
Application of Clausius Clapeyron Equation
Solid-Liquid Equilibrium – Freezing Point
The melting point or the freezing point of a substance is the temperature at which the solid and liquid phases of the substance co-exist in equilibrium. For this equilibrium, the Clapeyron equation can be written as,
Here, T is the melting point or the freezing point of the substance
VL is the molar volume of the liquid phase
Vs is the molar volume of the solid phase
ΔHf is the molar latent heat of fusion
i.e.,
dT/dP represents the rate of change of freezing point with external pressure P.
For substances like ice that contract on melting, the value of VL – VS becomes negative. As a result, dT/dP is negative. This means that the melting or freezing point of ice decreases with increases in pressure.
For substances like sulphur that expand on melting, the value of VL – VS becomes positive. As a result, dT/dP is positive. Therefore, the melting or freezing point of ice increases with increases in pressure.
Liquid-Vapour Equilibrium – Boiling Point
The boiling point temperature is the temperature at which the liquid and vapour phases of the substance co-exist in equilibrium. For this equilibrium, the Clapeyron equation can be written as,
Here,
VV and VL are the molar volumes of the vapour and liquid phases, respectively
T is the boiling point of the substance
ΔHv is the molar latent heat of vaporisation of the substance
dT/dP is the rate of change of boiling point with pressure
The volume Vv of the vapour phase of the given mass of a substance is always much greater than the liquid phase of the same substance. That is, dT/dP is always positive.
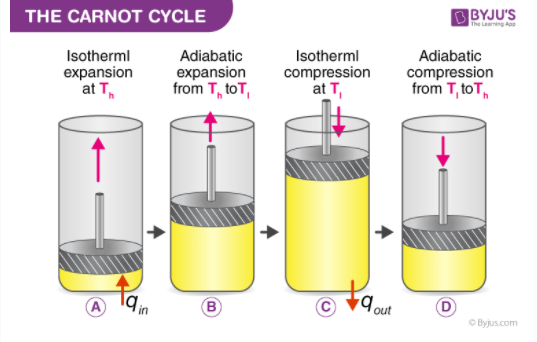
Carnot Engine
The theoretical thermodynamic cycle proposed by Sadi Carnot in 1824 is called the Carnot engine. He used a heat engine that performed a perfectly reversible cyclic process. No engine operating between a source and a sink at two given temperatures can be more efficient than a Carnot reversible engine operating between the same two temperatures. This is known as Carnot’s principle.
The working substance in a Carnot’s engine is taken through a reversible cycle of operations consisting of two isothermal and two adiabatic processes.
Refrigerator
It is a device that is used to keep bodies at a temperature lower than that of the surrounding.
Coefficient of performance
The amount of heat removed per unit of work done is called the coefficient of performance of a refrigerator.
Gibbs Free Energy (G)
A new thermodynamic state function G, the Gibbs free energy is defined as,
G = H – TS or ΔG = ΔH – TΔS (at constant temperature and pressure)
For a spontaneous reaction, ΔG must be negative. The use of Gibbs free energy has the advantage that it refers to the system only.
Third Law of Thermodynamics
The third law of thermodynamics states that “At absolute zero, the entropy of a perfectly crystalline substance is taken as zero”, which means that at absolute zero, every crystalline solid is in a state of perfect order, and its entropy should be zero. By virtue of the third law, the absolute value of entropy for a pure substance can be calculated at room temperature.
Points to Remember
- Thermodynamics deals with the energy relationships involving heat, mechanical energy and other forms of energy.
- Internal energy is the sum of the total kinetic energy and potential energy of the system.
- The concept of temperature is explained by the Zeroth law of thermodynamics.
- The first law of thermodynamics gives the relationship between heat transferred, the amount of work done and the change in the internal energy.
- Some of the thermodynamic processes are the isothermal process, adiabatic process, isobaric process and isochoric process.
- The specific heat capacity of a substance can be defined as the amount of heat required to raise the temperature of the unit mass of the substance through 10C.
- The second law of thermodynamics is stated by Kelvin-Planck and Clausius.
- The Heat engine is a machine that converts heat energy into mechanical energy.
- Enthalpy is given by the sum of the internal energy and the product of the pressure and volume of a thermodynamic system.
- The thermal energy per unit temperature that is not available for doing useful work is called entropy.
- The amount of heat removed per unit of work done is called the coefficient of performance of a refrigerator.
- The third law of thermodynamics states that “At absolute zero, the entropy of a perfectly crystalline substance is taken as zero.”
Top 15 Most Important and Expected JEE Questions of Thermodynamics

Solved Examples
1) Ideal gas is contained in a thermally insulated and rigid container, and it is heated through a resistance 100 Ω by passing a current of 1 A for five minutes; then, the change in internal energy of the gas is
a) zero
b) 30 kJ
c) 10 kJ
d) 20 kJ
Answer: b) 30 kJ
Solution:
Heat supplied to the gas container: H = i2 x R x dt
i = 1 A
R = 100 Ω
dt = 5 minutes = 300 sec
H = (1)2 x 100 x 300
= 30000 J = 30 kJ
dQ = dW + dU
Since the container is rigid, there is no work done when the gas expands,
Thus, dW = 0
Therefore, the amount of heat given to the system is equal to the change in internal energy
dQ = dU = 30 kJ.
2) 100 g of water is heated from 30° C to 50° C. Ignoring the slight expansion of the water, the change in its internal energy is (Specific heat of water is 4184 J/kg/K)
a) 8.4 kJ
b) 84 kJ
c) 2.1 kJ
d) 4.2 kJ
e) 3.2 kJ
Answer: a) 8.4 kJ
Solution:
Given,
m = 100 g
ΔT = (50 – 30) = 200
Specific heat of water, C = 4184 J/kg/K
ΔU = mCΔT
= 100 x 10-3 x 4184 x 20 = 8.4 kJ
3) Which of the following parameters does not characterise the thermodynamic state of matter?
a) Temperature
b) Pressure
c) Work
d) Volume
Answer: c) Work
Solution:
The work done does not characterise the thermodynamic state of matter. It will only give the relation between two different thermodynamic states.
4) When two moles of oxygen are heated from 0°C – 10°C at constant volume, its internal energy changes by 420 J. What is the molar specific heat of oxygen at constant volume?
a) 5.75 JK-1mol-1
b) 10.5 JK-1mol-1
c) 21 JK-1mol-1
d) 42 JK-1mol-1
Answer: c) 21 JK-1mol-1
Solution:
Given,
ΔT = 100C – 00C = 100C
ΔU = 420 J
n = 2
Internal energy, ΔU = nCvΔT
420 = 2 x Cv x 10
Cv = 21 JK-1mol-1
5) A gas is suddenly expanded such that its final volume becomes 3 times its initial volume. If the specific heat at the constant volume of the gas is 2R, then the ratio of initial to final pressure is nearly equal to
a) 5
b) 6.5
c) 7
d) 3.5
Answer: a) 5
Solution:
P1V1ץ = P2V2ץ
P2 = P1 (V1/V2)ץ
= 1 (⅓)3/2
= 3√3 = 5.1
Practice Problems
1) A given mass of a gas is compressed isothermally until its pressure is doubled. It is then allowed to expand adiabatically until its original volume is restored, and its pressure is then found to be 0.75 of its initial pressure. The ratio of the specific heat of the gas is approximately
a) 1.20
b) 1.41
c) 1.67
d) 1.83
2) Unit mass of a liquid volume V1 is completely changed into a gas of volume V2 at a constant external pressure p and temperature T. If the latent heat of evaporation for the given mass is L, then the increase in the internal energy of the system is
a) zero
b) p(V2 – V1)
c) L – p(V2 – V1)
d) L
3) A diatomic ideal gas is used in a car engine as the working substance. If, during the adiabatic expansion part of the cycle, the volume of the gas increases from V to 32 V, the efficiency of the engine is
a) 0.5
b) 0.75
c) 0.99
d) 0.25
4) Three designs are proposed for an engine operating between 500 K and 300 K. For 1 kcal of heat input, design A claims to produce 3000 J of work, design B claims to produce 2000 J of work and design C claims to produce 1680 J of work. The design which is possible
a) A only
b) B only
c) C only
d) All of these
5) A Carnot engine with a sink’s temperature at 17°C has 50% efficiency. By how much should its source temperature be changed to increase its efficiency to 60%?
a) 225 K
b) 128 0C
c) 580 K
d) 145 K
e) 145 0C
Thermodynamics Important Topics

Thermodynamics Important Questions

Thermodynamics Top 7 Questions

Thermodynamics JEE Solutions

Thermodynamics – Full Chapter Revision

Thermodynamics – Top 15 Most Important and Expected JEE Main Questions

Thermodynamics JEE Main Important Questions

Frequently Asked Questions
What are the different types of thermodynamic processes?
a) Isothermal Process
b) Adiabatic Process
c) Isochoric Process
d) Isobaric Process
What are the two significant statements of the second law of thermodynamics?
Kelvin-Planck’s Statement: It is impossible to derive a continuous supply of work by cooling a body to a temperature lower than that of the coolest of its surroundings.
Clausius Statement: It is impossible to make heat flow from a body at a lower temperature to a body at a higher temperature without doing any external work on the working substance.
Mention the different types of thermodynamic systems.
a) Open System
b) Closed System
c) Isolated System
What is a heat engine?
A machine that converts heat energy into mechanical energy is called a heat engine.
Define the Zeroth law of thermodynamics.
The law states that “Two systems in thermal equilibrium with a third system are also in thermal equilibrium with each other.”
Comments