What Is the Isochoric Process?
A thermodynamic process taking place at constant volume is known as the isochoric process. It is also called an isometric process or constant-volume process. The term isochoric has been derived from the Greek words “iso” meaning “constant” or “equal”, and “choric”, meaning “space” or “volume.”
An isochoric process is one for which,
In such a process, the work done is zero (since dW = P dV = 0 when V = constant). Hence, from the first law of thermodynamics,
dQ = dU (isochoric process)
The total heat supplied or rejected is also equal to the increase or decrease in the internal energy of the system.
Isochoric Process Example
A good example of an isochoric process is the ideal Otto cycle. In this, when the gasoline-air mixture is burnt in a car’s engine, there is an increase in the temperature and the pressure of the gas inside the engine. On the other hand, the volume of the gas remains exactly the same.
Also Read:
| Isothermal Process |
| Isobaric Process |
| Adiabatic Process |
Work Done by a Gas in an Isochoric Process
In an isochoric process, the volume of the gas remains constant. For example, suppose you have an ideal gas in a closed rigid container; heating the gas will raise its pressure without changing its volume. However, the quantity of gas remains constant. We can further deduce that the increase in energy is proportional to an increase in pressure and temperature.
This is represented by a vertical line on a P-V diagram. Since the volume does not change,
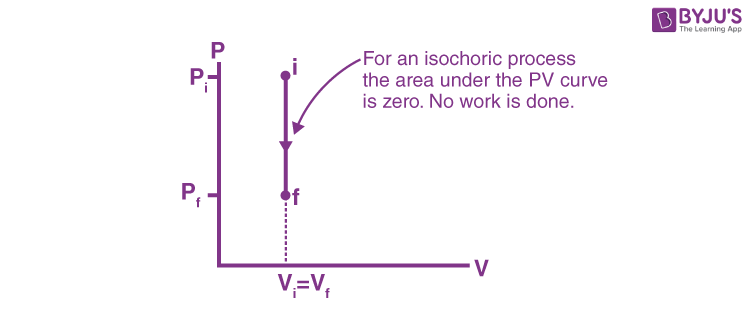
Whether the pressure change is positive or negative, the work done by the gas in an isochoric process is zero.
Work done by a gas in a process in which PVn = constant, where n is also constant.
Also Read: Thermodynamics

Comments