The photoelectric effect is a phenomenon in which electrons are ejected from the surface of a metal when light is incident on it. These ejected electrons are called photoelectrons. It is important to note that the emission of photoelectrons and the kinetic energy of the ejected photoelectrons is dependent on the frequency of the light that is incident on the metal’s surface. The process through which photoelectrons are ejected from the surface of the metal due to the action of light is commonly referred to as photoemission.
Download Complete Chapter Notes of Structure of Atom
Download Now
The photoelectric effect occurs because the electrons at the surface of the metal tend to absorb energy from the incident light and use it to overcome the attractive forces that bind them to the metallic nuclei. An illustration detailing the emission of photoelectrons as a result of the photoelectric effect is provided below.

Jump to
History of the Photoelectric EffectPrincipleFormulaLaws Governing the Photoelectric EffectExperimental Study of the Photoelectric EffectEinstien’s Photoelectric EquationGraphsApplicationsSolved Problems (Numericals)
Recommended Video
Photoelectric Effect – Basics

Hertz and Lenard’s Observation

History of the Photoelectric Effect
The photoelectric effect was first introduced by Wilhelm Ludwig Franz Hallwachs in the year 1887, and the experimental verification was done by Heinrich Rudolf Hertz. They observed that when a surface is exposed to electromagnetic radiation at a higher threshold frequency, the radiation is absorbed, and the electrons are emitted. Today, we study the photoelectric effect as a phenomenon that involves a material absorbing electromagnetic radiation and releasing electrically charged particles.
To be more precise, light incident on the surface of a metal in the photoelectric effect causes electrons to be ejected. The electron ejected due to the photoelectric effect is called a photoelectron and is denoted by e–. The current produced as a result of the ejected electrons is called photoelectric current.
Explaining the Photoelectric Effect: The Concept of Photons
The photoelectric effect cannot be explained by considering light as a wave. However, this phenomenon can be explained by the particle nature of light, in which light can be visualised as a stream of particles of electromagnetic energy. These ‘particles’ of light are called photons. The energy held by a photon is related to the frequency of the light via Planck’s equation.
E = h𝜈 = hc/λ
Where,
- E denotes the energy of the photon
- h is Planck’s constant
- 𝜈 denotes the frequency of the light
- c is the speed of light (in a vacuum)
- λ is the wavelength of the light
Thus, it can be understood that different frequencies of light carry photons of varying energies. For example, the frequency of blue light is greater than that of red light (the wavelength of blue light is much shorter than the wavelength of red light). Therefore, the energy held by a photon of blue light will be greater than the energy held by a photon of red light.
Threshold Energy for the Photoelectric Effect
For the photoelectric effect to occur, the photons that are incident on the surface of the metal must carry sufficient energy to overcome the attractive forces that bind the electrons to the nuclei of the metals. The minimum amount of energy required to remove an electron from the metal is called the threshold energy (denoted by the symbol Φ). For a photon to possess energy equal to the threshold energy, its frequency must be equal to the threshold frequency (which is the minimum frequency of light required for the photoelectric effect to occur). The threshold frequency is usually denoted by the symbol 𝜈th, and the associated wavelength (called the threshold wavelength) is denoted by the symbol λth. The relationship between the threshold energy and the threshold frequency can be expressed as follows.
Φ = h𝜈th = hc/λth
Relationship between the Frequency of the Incident Photon and the Kinetic Energy of the Emitted Photoelectron
Therefore, the relationship between the energy of the photon and the kinetic energy of the emitted photoelectron can be written as follows:
Ephoton = Φ + Eelectron
⇒ h𝜈 = h𝜈th + ½mev2
Where,
- Ephoton denotes the energy of the incident photon, which is equal to h𝜈
- Φ denotes the threshold energy of the metal surface, which is equal to h𝜈th
- Eelectron denotes the kinetic energy of the photoelectron, which is equal to ½mev2 (me = Mass of electron = 9.1*10-31 kg)
If the energy of the photon is less than the threshold energy, there will be no emission of photoelectrons (since the attractive forces between the nuclei and the electrons cannot be overcome). Thus, the photoelectric effect will not occur if 𝜈 < 𝜈th. If the frequency of the photon is exactly equal to the threshold frequency (𝜈 = 𝜈th), there will be an emission of photoelectrons, but their kinetic energy will be equal to zero. An illustration detailing the effect of the frequency of the incident light on the kinetic energy of the photoelectron is provided below.

From the image, it can be observed that
- The photoelectric effect does not occur when the red light strikes the metallic surface because the frequency of red light is lower than the threshold frequency of the metal.
- The photoelectric effect occurs when green light strikes the metallic surface, and photoelectrons are emitted.
- The photoelectric effect also occurs when blue light strikes the metallic surface. However, the kinetic energies of the emitted photoelectrons are much higher for blue light than for green light. This is because blue light has a greater frequency than green light.
It is important to note that the threshold energy varies from metal to metal. This is because the attractive forces that bind the electrons to the metal are different for different metals. It can also be noted that the photoelectric effect can also take place in non-metals, but the threshold frequencies of non-metallic substances are usually very high.
Einstein’s Contributions towards the Photoelectric Effect
The photoelectric effect is the process that involves the ejection or release of electrons from the surface of materials (generally a metal) when light falls on them. The photoelectric effect is an important concept that enables us to clearly understand the quantum nature of light and electrons.
After continuous research in this field, the explanation for the photoelectric effect was successfully explained by Albert Einstein. He concluded that this effect occurred as a result of light energy being carried in discrete quantised packets. For this excellent work, he was honoured with the Nobel Prize in 1921.
According to Einstein, each photon of energy E is
E = hν
Where E = Energy of the photon in joule
h = Plank’s constant (6.626 × 10-34 J.s)
ν = Frequency of photon in Hz
Properties of the Photon
- For a photon, all the quantum numbers are zero.
- A photon does not have any mass or charge, and they are not reflected in a magnetic and electric field.
- The photon moves at the speed of light in empty space.
- During the interaction of matter with radiation, radiation behaves as it is made up of small particles called photons.
- Photons are virtual particles. The photon energy is directly proportional to its frequency and inversely proportional to its wavelength.
- The momentum and energy of the photons are related, as given below
E = p.c where
p = Magnitude of the momentum
c = Speed of light
Definition of the Photoelectric Effect
Principle of the Photoelectric Effect
The law of conservation of energy forms the basis for the photoelectric effect.
Minimum Condition for Photoelectric Effect
Threshold Frequency (γth)
It is the minimum frequency of the incident light or radiation that will produce a photoelectric effect, i.e., the ejection of photoelectrons from a metal surface is known as the threshold frequency for the metal. It is constant for a specific metal but may be different for different metals.
If γ = Frequency of the incident photon and γth= Threshold frequency, then,
- If γ < γTh, there will be no ejection of photoelectron and, therefore, no photoelectric effect.
- If γ = γTh, photoelectrons are just ejected from the metal surface; in this case, the kinetic energy of the electron is zero.
- If γ > γTh, then photoelectrons will come out of the surface, along with kinetic energy.
Threshold Wavelength (λth)
During the emission of electrons, a metal surface corresponding to the greatest wavelength to incident light is known as threshold wavelength.
λth = c/γth
For wavelengths above this threshold, there will be no photoelectron emission. For λ = wavelength of the incident photon, then
- If λ < λTh, then the photoelectric effect will take place, and ejected electron will possess kinetic energy.
- If λ = λTh, then just the photoelectric effect will take place, and the kinetic energy of ejected photoelectron will be zero.
- If λ > λTh, there will be no photoelectric effect.
Work Function or Threshold Energy (Φ)
The minimal energy of thermodynamic work that is needed to remove an electron from a conductor to a point in the vacuum immediately outside the surface of the conductor is known as work function/threshold energy.
Φ = hγth = hc/λth
The work function is the characteristic of a given metal. If E = energy of an incident photon, then
- If E < Φ, no photoelectric effect will take place.
- If E = Φ, just a photoelectric effect will take place, but the kinetic energy of ejected photoelectron will be zero
- If E > photoelectron will be zero
- If E > Φ, the photoelectric effect will take place along with the possession of the kinetic energy by the ejected electron.
Photoelectric Effect Formula
According to Einstein’s explanation of the photoelectric effect,
The energy of photon = Energy needed to remove an electron + Kinetic energy of the emitted electron
i.e., hν = W + E
Where,
- h is Planck’s constant
- ν is the frequency of the incident photon
- W is a work function
- E is the maximum kinetic energy of ejected electrons: 1/2 mv²
Laws Governing the Photoelectric Effect
- For a light of any given frequency,; (γ > γ Th), the photoelectric current is directly proportional to the intensity of light.
- For any given material, there is a certain minimum (energy) frequency, called threshold frequency, below which the emission of photoelectrons stops completely, no matter how high the intensity of incident light is.
- The maximum kinetic energy of the photoelectrons is found to increase with the increase in the frequency of incident light, provided the frequency (γ > γ Th) exceeds the threshold limit. The maximum kinetic energy is independent of the intensity of light.
- The photo-emission is an instantaneous process.
Experimental Study of the Photoelectric Effect
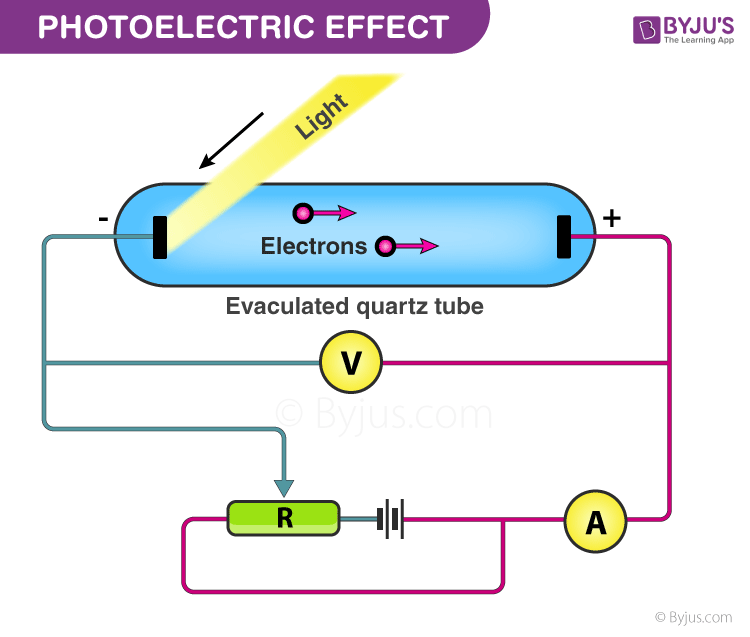
Photoelectric Effect: Experimental Setup
The given experiment is used to study the photoelectric effect experimentally. In an evacuated glass tube, two zinc plates, C and D, are enclosed. Plates C acts as an anode, and D acts as a photosensitive plate.
Two plates are connected to battery B and ammeter A. If the radiation is incident on plate D through a quartz window, W electrons are ejected out of the plate, and current flows in the circuit. This is known as photocurrent. Plate C can be maintained at desired potential (+ve or – ve) with respect to plate D.
Characteristics of the Photoelectric Effect
- The threshold frequency varies with the material, it is different for different materials.
- The photoelectric current is directly proportional to the light intensity.
- The kinetic energy of the photoelectrons is directly proportional to the light frequency.
- The stopping potential is directly proportional to the frequency, and the process is instantaneous.
Factors Affecting the Photoelectric Effect
With the help of this apparatus, we will now study the dependence of the photoelectric effect on the following factors:
- The intensity of incident radiation.
- A potential difference between the metal plate and collector.
- Frequency of incident radiation.
Effects of Intensity of Incident Radiation on Photoelectric Effect
The potential difference between the metal plate, collector and frequency of incident light is kept constant, and the intensity of light is varied.
The electrode C, i.e., the collecting electrode, is made positive with respect to D (metal plate). For a fixed value of frequency and the potential between the metal plate and collector, the photoelectric current is noted in accordance with the intensity of incident radiation.
It shows that photoelectric current and intensity of incident radiation both are proportional to each other. The photoelectric current gives an account of the number of photoelectrons ejected per sec.
Effects of Potential Difference between the Metal Plate and the Collector on the Photoelectric Effect
The frequency of incident light and intensity is kept constant, and the potential difference between the plates is varied.
Keeping the intensity and frequency of light constant, the positive potential of C is increased gradually. Photoelectric current increases when there is a positive increase in the potential between the metal plate and the collector up to a characteristic value.
There is no change in photoelectric current when the potential is increased higher than the characteristic value for any increase in the accelerating voltage. This maximum value of the current is called saturation current.
Effect of Frequency on Photoelectric Effect
The intensity of light is kept constant, and the frequency of light is varied.
For a fixed intensity of incident light, variation in the frequency of incident light produces a linear variation of the cut-off potential/stopping potential of the metal. It is shown that the cut-off potential (Vc) is linearly proportional to the frequency of incident light.
The kinetic energy of the photoelectrons increases directly proportionally to the frequency of incident light to completely stop the photoelectrons. We should reverse and increase the potential between the metal plate and collector in (negative value) so the emitted photoelectron can’t reach the collector.
Einstein’s Photoelectric Equation
According to Einstein’s theory of the photoelectric effect, when a photon collides inelastically with electrons, the photon is absorbed completely or partially by the electrons. So if an electron in a metal absorbs a photon of energy, it uses the energy in the following ways.
Some energy Φ0 is used in making the surface electron free from the metal. It is known as the work function of the material. Rest energy will appear as kinetic energy (K) of the emitted photoelectrons.
Einstein’s Photoelectric Equation Explains the Following Concepts
- The frequency of the incident light is directly proportional to the kinetic energy of the electrons, and the wavelengths of incident light are inversely proportional to the kinetic energy of the electrons.
- If γ = γth or λ =λth then vmax = 0
- γ < γth or λ > λth: There will be no emission of photoelectrons.
- The intensity of the radiation or incident light refers to the number of photons in the light beam. More intensity means more photons and vice-versa. Intensity has nothing to do with the energy of the photon. Therefore, the intensity of the radiation is increased, and the rate of emission increases, but there will be no change in the kinetic energy of electrons. With an increasing number of emitted electrons, the value of the photoelectric current increases.
Different Graphs of the Photoelectric Equation
- Photoelectric current vs Retarding potential for different voltages
- Photoelectric current vs Retarding potential for different intensities
- Electron current vs Light Intensity
- Stopping potential vs Frequency
- Electron current vs Light frequency
- Electron kinetic energy vs Light frequency






Applications of the Photoelectric Effect
- Used to generate electricity in solar panels. These panels contain metal combinations that allow electricity generation from a wide range of wavelengths.
- Motion and Position Sensors: In this case, a photoelectric material is placed in front of a UV or IR LED. When an object is placed in between the Light-emitting diode (LED) and sensor, light is cut off, and the electronic circuit registers a change in potential difference
- Lighting sensors, such as the ones used in smartphones, enable automatic adjustment of screen brightness according to the lighting. This is because the amount of current generated via the photoelectric effect is dependent on the intensity of light hitting the sensor.
- Digital cameras can detect and record light because they have photoelectric sensors that respond to different colours of light.
- X-Ray Photoelectron Spectroscopy (XPS): This technique uses X-rays to irradiate a surface and measure the kinetic energies of the emitted electrons. Important aspects of the chemistry of a surface can be obtained, such as elemental composition, chemical composition, the empirical formula of compounds and chemical state.
- Photoelectric cells are used in burglar alarms.
- Used in photomultipliers to detect low levels of light.
- Used in video camera tubes in the early days of television.
- Night vision devices are based on this effect.
- The photoelectric effect also contributes to the study of certain nuclear processes. It takes part in the chemical analysis of materials since emitted electrons tend to carry specific energy that is characteristic of the atomic source.
Photoelectric Effect – JEE Advanced Concepts and Problems

Problems on the Photoelectric Effect
1. In a photoelectric effect experiment, the threshold wavelength of incident light is 260 nm and E (in eV) = 1237/λ (nm). Find the maximum kinetic energy of emitted electrons.
Solution:
Kmax = hc/λ – hc/λ0 = hc × [(λ0 – λ)/λλ0]
⇒ Kmax = (1237) × [(380 – 260)/380×260] = 1.5 eV
Therefore, the maximum kinetic energy of emitted electrons in the photoelectric effect is 1.5 eV.
2. In a photoelectric experiment, the wavelength of the light incident on metal is changed from 300 nm to 400 nm and (hc/e = 1240 nm-V). Find the decrease in the stopping potential.
Solution:
hc/λ1 = ϕ + eV1 . . . . (i)
hc/λ2 = ϕ + eV2 . . . . (ii)
Equation (i) – (ii)
hc(1/λ1 – 1/λ2) = e × (V1 – V2)
⇒V1 – V2 = (hc/e) × [(λ2 – λ1)/(λ1 λ2)]
= (1240 nm V) × 100nm/(300nm × 400nm)
=12.4/12 ≈ 1V
Therefore, the decrease in the stopping potential during the photoelectric experiment is 1V.
3. When ultraviolet light with a wavelength of 230 nm shines on a particular metal plate, electrons are emitted from plate 1, crossing the gap to plate 2 and causing a current to flow through the wire connecting the two plates. The battery voltage is gradually increased until the current in the ammeter drops to zero, at which point the battery voltage is 1.30 V.

a) What is the energy of the photons in the beam of light in eV?
b) What is the maximum kinetic energy of the emitted electrons in eV?
Solution:
Assuming that the wavelength corresponds to the wavelength in the vacuum.
f = 1.25 × 1015 Hz
The energy of photon E = hf
E = (4.136 × 10-15)( 1.25 × 1015)
Note: Planck’s constant in eV s = 4.136 × 10-15 eV s
E = 5.17 eV.
b) The maximum kinetic energy related to the emitted electron is stopping potential. In this case, the stopping potential is 1.30V. So the maximum kinetic energy of the electrons is 1.30V.
Also Check out: JEE Main Photoelectric Effect Previous Year Questions with Solutions
Important Points to Remember
- If we consider the light with any given frequency, the photoelectric current is generally directly proportional to the intensity of light. However, the frequency should be above the threshold frequency in such a case.
- Below threshold frequency, the emission of photoelectrons completely stops despite the high intensity of incident light.
- A photoelectron’s maximum kinetic energy increases with an increase in the frequency of incident light. In this case, the frequency should exceed the threshold limit. Maximum kinetic energy is not affected by the intensity of light.
- Stopping potential is the negative potential of the opposite electrode when the photo-electric current falls to zero.
- The threshold frequency is described as the frequency when the photoelectric current stops below a particular frequency of incident light.
- The photoelectric effect establishes the quantum nature of radiation. This has been taken into account to be proof in favour of the particle nature of light.

Comments