Alternate Interior Angles

Alternate interior angles are the angles formed when a transversal intersects two coplanar lines. They lie on the inner side of the parallel lines but on the opposite sides of the transversal. The transversal crosses through the two lines which are Coplanar at separate points. These angles represent whether the two given lines are parallel to each other or not. If these angles are equal to each other then the lines crossed by the transversal are parallel. In this article, we will discuss what are alternate interior angles, the theorem statements and proofs based on the alternate interior angles, what is a co-interior angle, and many solved examples.

Table of Contents:

• What is an Alternate Interior Angle?
• Properties
• Theorems and Proofs
• Antithesis of the Theorem
• Co-interior Angles
• Co-interior Angle Theorem and Proof
• Solved Examples
• FAQs

Alternate Interior Angles Definition

The angles which are formed inside the two parallel lines, when intersected by a transversal, are equal to its alternate pairs. These angles are called alternate interior angles.

In the above-given figure, you can see, two parallel lines are intersected by a transversal. Therefore, the alternate angles inside the parallel lines will be equal.

i,e. ∠A = ∠D and ∠B = ∠C

Properties

• These angles are congruent.
• The sum of the angles formed on the same side of the transversal which are inside the two parallel lines is always equal to 180°.
• In the case of non – parallel lines, alternate interior angles don’t have any specific properties.

Theorem and Proof

Statement: The theorem states that “ if a transversal crosses the set of parallel lines, the alternate interior angles are congruent”.

Given: a//d

To prove: ∠4 = ∠5 and ∠3 = ∠6

Proof: Suppose a and d are two parallel lines and l is the transversal that intersects a and d at points P and Q. See the figure given below.

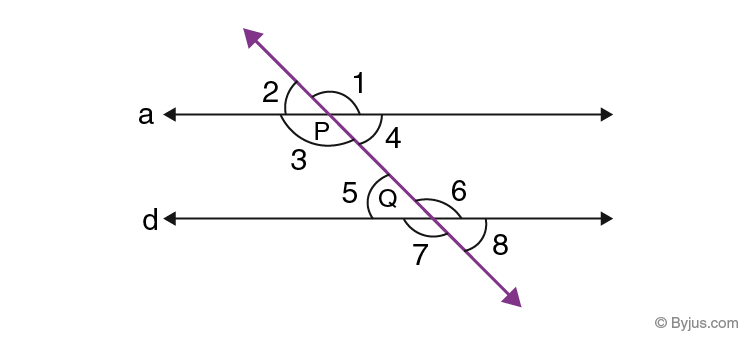
From the properties of the parallel line, we know if a transversal cuts any two parallel lines, the corresponding angles and vertically opposite angles are equal to each other. Therefore,

∠2 = ∠5 ………..(i) [Corresponding angles]

∠2 = ∠4 ………..(ii) [Vertically opposite angles]

From eq.(i) and (ii), we get;

∠4 = ∠5 [Alternate interior angles]

Similarly,

∠3 = ∠6

Hence, it is proved.

Antithesis of Theorem

If the alternate interior angles produced by the transversal line on two coplanar are congruent, then the two lines are parallel to each other.

Given: ∠4 = ∠5 and ∠3 = ∠6

To prove: a//b

Proof: Since ∠2 = ∠4 [Vertically opposite angles]

So, we can write,

∠2 = ∠5, which are corresponding angles.

Therefore, a is parallel to b.

Co-interior Angles

Co-interior angles or Consecutive interior angles are the two angles that are on the same side of the transversal. Co-interior angles are the interior angles and it sums up to 180 degrees. It means that the sum of two interior angles, which are on the same side of transversal is supplementary. Co-interior angles resemble like in “C” shape and both the angles are not equal to each other. The co-interior angle is also known as the consecutive interior angles or the same side interior angles.

Co-interior Angle Theorem and Proof

Statement:
If the transversal intersects the two parallel lines, each pair of co-interior angles sums up to 180 degrees (supplementary angles).

Proof:

Let us consider the image given above:

In the figure, angles 3 and 5 are the co interior angles and angles 4 and 6 are the co-interior angles.

To prove: ∠3 and ∠5 are supplementary and ∠4 and ∠6 are supplementary.

Given that, a and b are parallel to each other and t is the transversal. 

By the definition of linear pair, 

∠1 and ∠3 form the linear pair.

Similarly, ∠2 and ∠4 form the linear pair.

By using the supplement postulate,

∠1 and ∠3 are supplementary

(i.e.) ∠1 + ∠3 = 180

Similarly, 

∠2 and ∠4 are supplementary

(i.e.) ∠2 + ∠4 = 180

By using the corresponding angles theorem, we can write

∠1 ≅∠5 and ∠2 ≅ ∠6

Thus, by using the substitution property, we can say, 

∠3 and ∠5 are supplementary and ∠4 and ∠6 are supplementary.

Hence, the co-interior angle theorem (consecutive interior angle) is proved.

The converse of this theorem is “if a transversal intersects two lines, such that the pair of co-interior angles are supplementary, then the two lines are parallel”.

Facts about consecutive interior or co-interior angles:

• Consecutive interior or co-interior angles contains different vertices but lie on the same side of the transversal
• These angles lie between two lines
• Consecutive interior angles are non-adjacent angles
• If a transversal is drawn on two parallel lines, then the sum of co-interior angles formed are always added up to 180 degrees
• The sum of consecutive interior angles of a parallelogram is always supplementary

Examples

Question 1:

Find the value of B and D in the given figure.

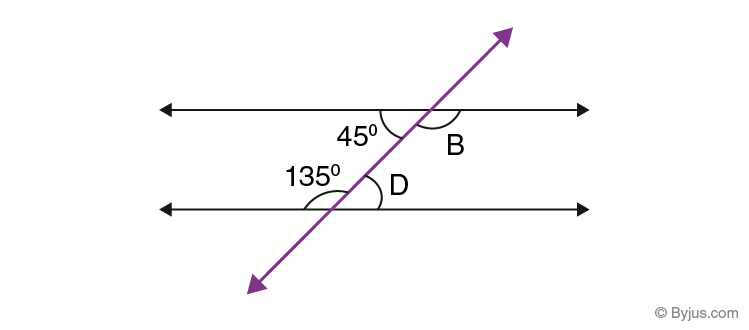
Solution:

Since 45° and D are alternate interior angles, they are congruent.

So, D = 45°

Since 135° and B are alternate interior angles, they are congruent.

So, B = 135°

Question 2:

Find the missing angles A, C and D in the following figure.

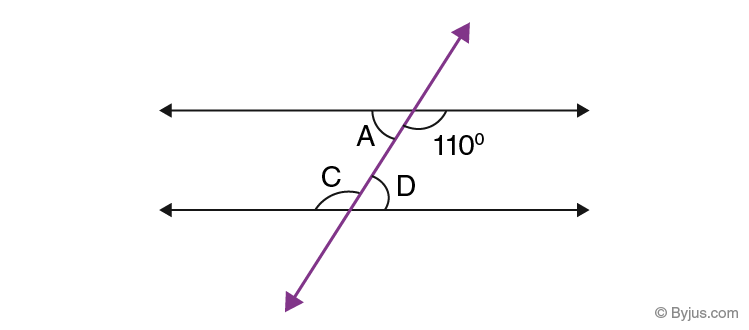
Solution:

 As angles ∠A, 110°, ∠C and ∠D are all alternate interior angles, therefore;

∠C = 110°

By supplementary angles theorem, we know;

∠C+∠D = 180°

∠D = 180° – ∠C = 180° – 110° = 70°

Since,

∠A = ∠D

Therefore, ∠A = 70°.

Example 3:

Find the value of x from the given below figure.

Solution:

We know that alternate interior angles are congruent.

Therefore, 4x – 19 = 3x + 16

4x – 3x = 19+16

x = 35

Video Lesson on Intersecting and Parallel lines

Download the BYJU’S App and get a better learning experience with the help of personalised videos.