Factors of 64 are the natural numbers that can divide the original number evenly. For example, 2 is a factor of 64 because 64 divided by 2 is equal to 32. When two factors are multiplied together and they result in the original number, then they are called pair factors. By factorisation method, we can find the factors of 64.
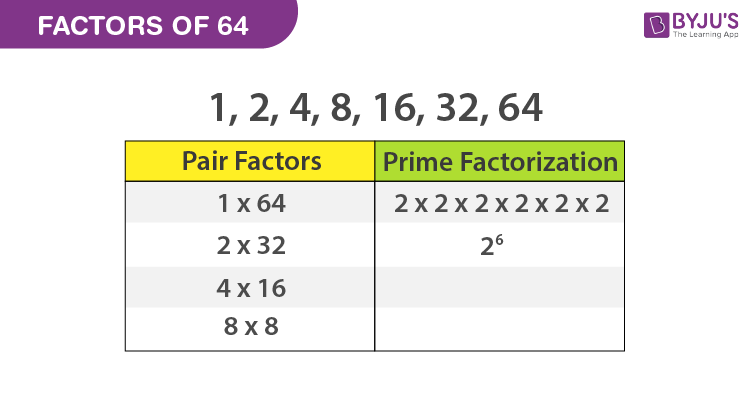
Pair Factors of 64
To find the factor pairs of 64, multiply the two numbers in a pair to get the original number as 64, such numbers are as follows:
If 1 × 64 = 64, then (1, 64) is a pair factor of 64.
2 × 32 = 64, (2, 32) is a pair factor of 64
4 × 16 = 64, then (4, 16) is a pair factor of 64
8 × 8 = 64, (8, 8) is a pair factor of 64
Therefore, the positive pair factors are (1, 64), (2, 32), (4,16) and (8, 8)
To find the negative pair factors of 64, then proceed with the following steps
-1 × -64 = 64, (-1, -64) is a pair factor of 64.
-2 × -32 = 64, (-2, -32) is a pair factor of 64
-4 × -16 = 64, then (-4, -16) is a pair factor of 64
-8 × -8 = 64, (-8, -8) is a pair factor of 64
Therefore, the negative pair factors are (-1, -64), (-2,-32), (-4, -16) and (-8, -8).
How to calculate the Factors of 64?
To find the factors of 64 we need to divide the original number by all the natural numbers from 1 to 64. The numbers that divide 64 completely, without leaving any remainder, are the required factors.
64 ÷ 1 = 64
64 ÷ 2 = 32
64 ÷ 4 = 16
64 ÷ 8 = 8
64 ÷ 16 = 4
64 ÷ 32 = 2
64 ÷ 64 = 1
| Factors of 64 |
| 1, 2, 4, 8, 16, 32 and 64 |
Prime Factors of 64 By Division Method
The number 64 is a composite and it should have prime factors. Now let us know how to calculate the prime factors of a number 64.
Step 1: The first step is to divide the number 64 with the smallest prime factor, say 2.
64 ÷ 2 = 32
Step 2: Again divide 32 by 2 and the process goes on.
32 ÷ 2 = 16
16 ÷ 2 = 8
8 ÷ 2 = 4
4 ÷ 2 = 2
2 ÷ 2 = 1
Finally, we received the number 1 at the end of the division process. So that we cannot proceed further. So, the prime factors of 64 are written as 2 x 2 × 2 x 2 x 2 x 2 or 26, where 2 is a prime number.
It is possible to find the exact number of factors of a number 64 with the help of prime factorisation. The prime factor of the 64 is 26. The exponent in the prime factorisation is 6. When you add the number 1 with the exponent 6, we get 7. i.e.,6 +1 = 7. Therefore, the number 64 has 7 factors.
Video Lesson on Prime Factors

Solved Examples
Q.1: Find the sum of all the factors of number 64 and check whether it is odd or even?
Solution: The factors are 1, 2, 4, 8, 16, 32 and 64. Now by adding these factors together we get;
1+2+4+8+16+32+64 = 127
Hence, 127 is an odd number.
Q.2: A black board has an area of 64 sq.cm. If the length of the board is 8 cm, then find its width.
Solution: Given,
Area of the board = 64 sq cm.
Given, length = 8 cm
A board can be either rectangular or square.
Therefore, area will be the product of the length and width.
Area = length x width
Width = area ÷ length
= 64 ÷ 8
= 8
Therefore, width is also equal to 8 cm. So, we can conclude that the blackboard is in square shape.
Q.3: Jack studies daily for 4 hours. In how many days he will cover 64 hours?
Solution: Number of hours Jack studies daily = 4 hours
Total number of hours = 64 hours
Therefore, number of days to cover 64 hours = 64/4 = 16
Hence, if Jack studies 4 hours for 16 days, he will cover 64 hours.
Q.4: List the common factors between 64, 100 and 140.
Solution: To find the common factors we need to lsit down the factors of each number here.
Factors of 64 = 1, 2, 4, 8, 16, 32, 64
Factors of 100 = 1, 2, 4, 5, 10, 20, 25, 50, 100
Factors of 140 = 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140
Common factors of 64, 100 and 140 = 1, 2 and 4.
Stay tuned with BYJU’S to know about factor 64 and the factors and prime factors of other numbers. Download BYJU’S – The Learning App for better experience and clarification and also watch interactive videos.
Frequently Asked Questions – FAQs
What are the factors of 64?
What are the first ten multiples of 64?
What is the largest factor of 64?
What are the odd factors of 64?
What are the common factors of 128 and 64?
| Links Related to Factors | |
| Factors of 8 | Factor of 36 |
| Factors of 48 | Factors of 18 |
| Factors of 24 | Factors of 25 |
| Factors of 42 | Factors of 60 |
| Factors of 35 | Factors of 81 |
| Factors of 75 | Factors of 56 |


4-7=0+666666