In trigonometry, there are three major or primary ratios, Sine, Cosine and Tangent, which are used to find the angles and length of the right-angled triangle. Before discussing Sin 60 degrees, let us know the importance of Sine function in trigonometry. Sine function defines a relation between the angle(formed between the hypotenuse and adjacent side) and the opposite side to the angle and hypotenuse. Or you can say, the Sine of angle theta is equal to the ratio of perpendicular and hypotenuse of a right-angled triangle.
The trigonometry ratios sin, cos and tan for an angle are the primary functions. The value of sin 60 degrees and other trigonometry ratios for all the degrees 0°, 30°, 45°, 90°,180° are generally used in trigonometry equations. These values are easy to memorize with the help trigonometry table. Let us discuss the value of sine 60 degrees here in this article.
Also, read:
Value of Sin 60 Degree
In a right-angled triangle, the sine of angle α is a ratio of the length of the opposite side(perpendicular) to the length of the hypotenuse side.

Sin α= Opposite Side/Hypotenuse
=Perpendicular Side/Hypotenuse Side
= a/h
So, the ratio sin 60 degrees function will be, sin 60 = Perpendicular/Hypotenuse
There is a simple method by means of which we can calculate the value of sine ratios for all the degrees. If you learn this method, you can easily calculate the values for all other trigonometry ratios. So, let’s start with calculating the values for sin 0°, sin 30°, sin 45°, sin 60°, sin 90°.
From the above equations, we get sin 60 degrees exact value as √3/2. In the same way, we can find the values for cos and tan ratios.
Therefore, the exact value of sin 60 degrees is √3/2
Cos 0° = Sin 90° = 1
Cos 30°= Sin 60° = √3/2
Cos 45° = Sin 45° = 1/√2
Cos 60° = Sin 30° =1/2
Cos 90° = Sin 0° = 0
Also,
Tan 0° = Sin 0°/Cos 0° = 0
Tan 30° = Sin 30°/Cos 30° =1/√3
Tan 45° = Sin 45°/Cos 45° = 1
Tan 60° = Sin 60°/Cos 60° = √3
Tan 90° = Sin 90°/Cos 90°= ∞
The above values of trigonometry ratios are with respect to degrees. We can also mention the values with respect to radians. Radians is considered for unit circle, whose radius is equal to one. The radian is denoted by π.
For 0°, the value of radian is 0. In the same way, we can create a table for trigonometry ratios with respect to π.
| Radian | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| Sin | 0 | 1/2 | \(\begin{array}{l}1/\sqrt{2}\end{array} \) |
\(\begin{array}{l}\sqrt{3}/2\end{array} \) |
1 | 0 | -1 | 0 |
| Cos | 1 | \(\begin{array}{l}\sqrt{3}/2\end{array} \) |
\(\begin{array}{l}1/\sqrt{2}\end{array} \) |
1/2 | 0 | -1 | 0 | 1 |
| Tan | 0 | \(\begin{array}{l}1/\sqrt{3}\end{array} \) |
1 | \(\begin{array}{l}\sqrt{3}\end{array} \) |
Undefined | 0 | Undefined | 0 |
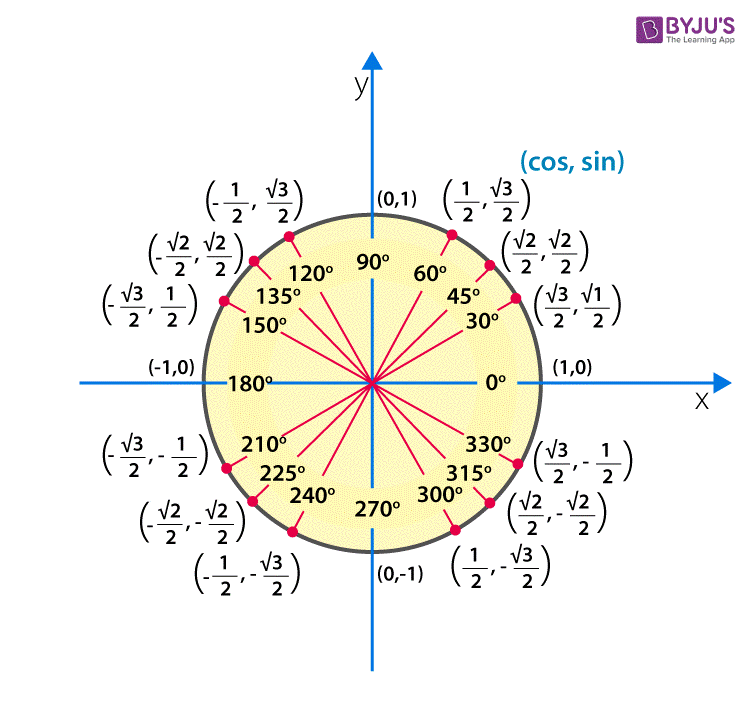
We learned about sin 60 degrees value along with other degree values here, this far. Also, derived the value for cos degree and tan degrees with respect sin degrees and also in terms of radians. In the same way, we can find the values for other trigonometric ratios like sec, cosec and cot.
Learn more about trigonometric ratios and identities and download BYJU’S-The Learning App for a better experience.

Comments