The trigonometric functions relate the angles of a triangle to the length of its sides. Trigonometric functions are important in the study of periodic phenomena like sound and light waves and many other applications. The most familiar three trigonometric ratios are sine function, cosine function and tangent function. For angles less than a right angle, trigonometric functions are commonly defined as the ratio of two sides of a right triangle containing the angle and their values can be found in the length of various line segments around a unit circle.
| Sin 90 degrees = 1 |
The angles are calculated with respect to sin, cos and tan functions which are the primary functions, whereas cosecant, secant and cot functions are derived from the primary functions. Usually, the degrees are considered as 0°, 30°, 45°, 60°, 90°, 180°, 270° and 360°. Here, you will learn the value for sin 90 degrees and how the values are derived along with other degrees or radian values.
Sine 90 degrees value
To define the sine function of an acute angle, start with the right-angled triangle ABC with the angle of interest and the sides of a triangle. The three sides of the triangle are given as follows:
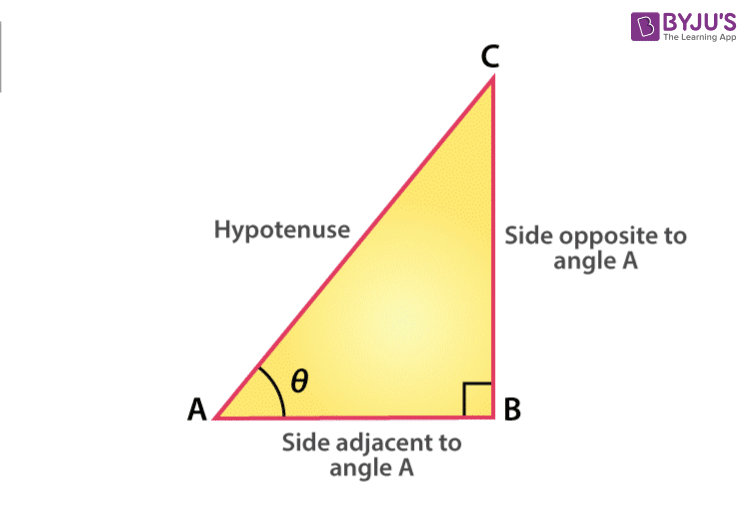
- The opposite side – side opposite to the angle of interest.
- The hypotenuse side – opposite side of the right angle and it is always the longest side of a right triangle
- The adjacent side – remaining side of a triangle and it forms a side of both the angle of interest and the right angle
The sine function of an angle is equal to the length of the opposite side divided by the length of the hypotenuse side and the formula is given by
The sine law states that the sides of a triangle are proportional to the sine of the opposite angles.
In the following cases, the sine rule is used. Those conditions are
Case 1: Given two angles and one side (AAS and ASA)
Case 2: Given two sides and non included angle (SSA)
Derivation to Find the Value of Sin 90 Degrees
Let us now calculate the value of sin 90°. Consider the unit circle. That is the circle with radius 1 unit and its centre placed in origin.

From the basic knowledge of trigonometry, we conclude that for the given right-angled triangle, the base measuring ‘x’ units and the perpendicular measuring ‘y’ units.
We know that,
For any right-angled triangle measuring with any of the angles, sine functions equal to the ratio of the length of the opposite side to the length of the hypotenuse side. So, from the figure
Start measuring the angles from the first quadrant and end up with 90° when it reaches the positive y-axis. Now the value of y becomes 1 since it touches the circumference of the circle. Therefore the value of y becomes 1.
Therefore, sin 90 degree equals to the fractional value of 1/ 1.
Sin 90° = 1
The most common trigonometric sine functions are
Sin 90 degree plus theta
Sin 90 degree minus theta
Some other trigonometric sine identities are as follows:
- \(\begin{array}{l}\sin x=\frac{1}{\csc x}\end{array} \)
- \(\begin{array}{l}\sin^{2}x+\cos ^{2}x=1\end{array} \)
- \(\begin{array}{l}\sin (-x)=-\sin x\end{array} \)
- Sin 2x = 2 sin x cos x
In the same way, we can derive other values of sin angles like 0°, 30°,45°,60°,90°,180°,270° and 360°. Below is the trigonometry table, which defines all the values of sine along with other trigonometric ratios.
| Trigonometry Ratio Table | ||||||||
| Angles (In Degrees) | 0 | 30 | 45 | 60 | 90 | 180 | 270 | 360 |
| Angles (In Radians) | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | −1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | −1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | Not Defined | 0 | Not Defined | 0 |
| cot | Not Defined | √3 | 1 | 1/√3 | 0 | Not Defined | 0 | Not Defined |
| cosec | Not Defined | 2 | √2 | 2/√3 | 1 | Not Defined | −1 | Not Defined |
| sec | 1 | 2/√3 | √2 | 2 | Not Defined | −1 | Not Defined | 1 |
Cos 0 Degrees
The value of cos 0 degrees is equal to the value of sin 90 degrees.
Sin 90° = Cos 0° = 1
Solved Examples
Question 1: Find the value of sin 135°.
Solution:
Given, sin 135° = sin ( 90° + 45° )
= 1 /√2
Therefore, the value of sin 135° is 1 /√2
Question 2: Find the value of cos 30°.
Solution:
Given , cos 30° = cos ( 90° – 60° )
Therefore, the value of cos 30° is √3/2.
Practice Questions
- Evaluate the value of sin 90° + Cos 90°.
- Find the value of 2sin 90° – sec 90°
- What is the value of (sin 90°)/2 – sin 30°?
Keep visiting BYJU’S for more information on trigonometric ratios and its related articles, and also watch the videos to clarify the doubts.
| Related Links | |
| Cosine Function | Trigonometry Formulas |
| Inverse Cosine | Law of Sines Formula |
Frequently Asked Questions – FAQs
What is the exact value of sin 90 degrees?
What is the value of hypotenuse of sin 90 is 1 and opposite side is equal to 5 units?
Sin (angle) = Opposite side/Hypotenuse
Sin 90 = 5/Hypotenuse
1 = 5/H
Hypotenuse = 5/1
Hypotenuse = 5.
How do we write sin 90 degrees in radians?
Sin 90° = Sin π/2 = 1
How to find the value of cos 90 degrees with the help of sin 90 degrees?
Since, Sin2 θ + Cos2 θ = 1
Therefore,
Sin2 90° + Cos2 90° = 1
12 + cos2 90° = 1
Cos2 90° = 1 – 1 = 0
Cos 90° = 0
What is sin 90 minus theta?
Sin (90 – θ) = Cos θ


Comments