Linear inequalities in two variables are the inequalities composed of two algebraic expressions related by the symbol ‘<’, ‘>’, ‘≤’ or ‘≥’. Some of the linear inequalities in two variables are:
ax + by < c
ax + by > c
ax + by ≤ c
ax + by ≥ c
ax2 + bx + c ≤ 0
ax2 + bx + c ≥ 0
These are linear inequalities in two variables x and y when a ≠ 0, b ≠ 0. A system of linear inequalities in two variables consists of two or more linear inequalities containing the same variables.
Learn more about linear inequalities in two variables here.
The solution of a linear inequality is the ordered pair that is a solution to all inequalities in the system. However, the solution of a system of linear inequalities in two variables can be obtained in two methods, namely graphical and non-graphical methods. Among these two methods, the graphical method of solving inequalities is the most effective one.
|
Read more: |
|---|
Let’s have a look at the graphical method of solving given inequalities in two variables.
Graphing Solution of System of Linear Inequalities in Two Variables
The graphical method of solving the system of inequalities involves the following steps.
Step 1: Plot all the lines of inequalities for the given system of linear inequalities, i.e. two or more inequalities on the same Cartesian plane.
Step 2: If inequality is of the type ax + by ≥ c or ax + by ≤ c, then the points on the line ax + by = c are also included in the solution region. Here, we have to draw a dark line in the solution region.
Step 3: If inequality is of the form ax + by > c or ax + by < c, then the points on the line ax + by = c are excluded in the solution region. In this case, we need to draw a broken or dotted line in the solution region.
Step 4: The double or triple shaded region (as per the number of lines of inequalities), common to the concerned shaded regions, is the required solution region for the given system of linear inequalities. Also, this solution of a system of linear inequalities could be either of the following.
- open or unbounded
- closed or bounded
- no solution
Go through the solved problems of solving a system of linear inequalities in two variables given below.
Solving Problems Involving System of Linear Inequalities in Two Variables
Question 1: Solve the following system of linear inequalities in a graphical method.
4x + 5y ≤ 40,
x ≥ 3,
y ≥ 2
Solution:
Given,
4x + 5y ≤ 40,
x ≥ 3,
y ≥ 2
Consider the equation 4x + 5y = 40
5y = 40 – 4x
y = (40 – 4x)/5
|
x |
0 |
5 |
10 |
|---|---|---|---|
|
y |
8 |
4 |
0 |
Now, we have to draw the graph of the lines 4x + 5y = 40, x = 3 and y = 2.
For 4x + 5y ≤ 40, shade the region below the line of 4x + 5y = 40.
For x ≥ 3, shade the region towards the right side of the line x = 3.
For y ≥ 2, shade the region towards the up over the line y = 2 as shown in the below graph.
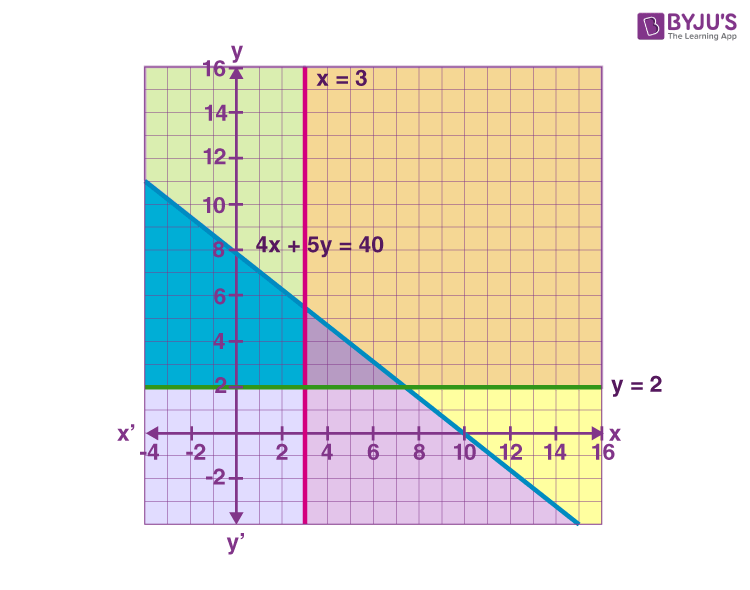
Hence, shaded regions including all the points on the lines are also the solution of the given system of linear inequalities.
For the given system of inequalities, the solution is a closed or bounded type of solution. That means, the solution region is enclosed by all the lines of inequalities.
Question 2:
Solve the system of linear inequalities given below:
x + 2y ≥ 6,
2x + y > 6,
x ≥ 0,
y ≥ 0
Solution:
Given,
x + 2y ≥ 6,
2x + y > 6,
x ≥ 0,
y ≥ 0
Consider the equation x + 2y = 6
2y = 6 – x
y = (6 – x)/2
|
x |
0 |
2 |
6 |
|---|---|---|---|
|
y |
3 |
2 |
0 |
Now, consider another equation 2x + y = 6
y = 6 – 2x
|
x |
0 |
2 |
3 |
|---|---|---|---|
|
y |
6 |
2 |
0 |
Let us plot these points on the graph and shade the region as per the inequality symbol.
For x + 2y ≥ 6, shade the region above the solid line of the equation x + 2y = 6.
For 2x + y > 6, shade the region above the dotted line of the equation 2x + y = 6.
For x ≥ 0, y ≥ 0, we need to consider the x and y-axis and shade accordingly as shown in the below figure.
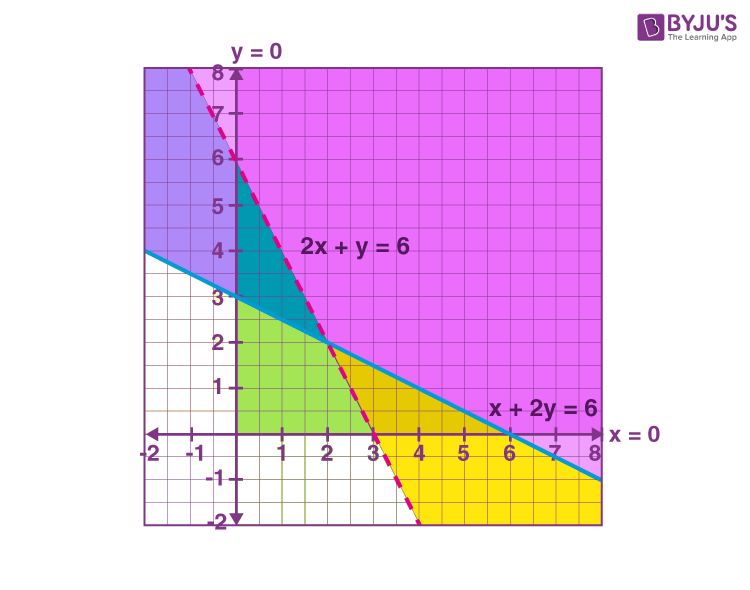
Hence, shaded regions including all the points in the first quadrant (since x ≥ 0 and y ≥ 0) and on the line x + 2y = 6 but not on the line 2x + y = 6 are the solution of the given system of linear inequalities.
For the given system of inequalities, the solution is an open or unbounded type of solution. That means, the solution region is not enclosed by all the lines of inequalities.
Question 3:
Solve the system of linear inequalities given below:
x − 2y ≤ 3
3x − 6y ≥ 15
Solution:
Given,
x − 2y ≤ 3
3x − 6y ≥ 15
For x − 2y ≤ 3, y ≥ (½) x + (-3/2)
For 3x – 6y ≥ 12, y ≤ (½) x + (-5/2)
The graph of these inequalities is given as:
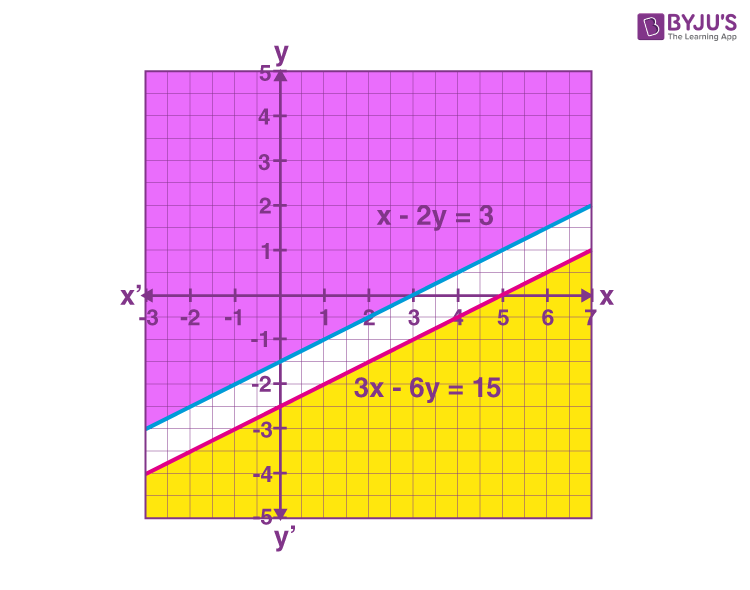
Hence, there is no common shaded region for the given inequalities. Thus, there is no solution for the given system of inequalities.
The non-graphical method of solving the system of linear inequalities in two variables involves identifying the point of intersection of the two or more inequalities by solving them. It could be possible when there is no intersection point among them.

Comments