Linear inequalities in two variables represent the inequalities between two algebraic expressions where two distinct variables are included. In linear inequalities in two variables, we use greater than (>), less than (<), greater than or equal (≥) and less than or equal (≤) symbols, instead of using equal to a symbol (=).
What is Linear Inequalities?
Any two real numbers or two algebraic expressions associated with the symbol ‘<’, ‘>’, ‘≤’ or ‘≥’ form a linear inequality. For example, 9<11, 18>17 are examples of numerical inequalities and x+7>y, y<10-x, x ≥ y > 11 are examples of algebraic inequalities.
The symbols ‘<‘ and ‘>’ represent the strict inequalities and the symbols ‘≤’ and ‘≥’ represent slack inequalities. To represent linear inequalities in one variable in a number line is a visual representation and is a convenient way to represent the solutions of the inequality. Now, we will discuss the graph of a linear inequality in two variables.
What are Linear Inequalities in Two Variables?
Linear inequalities in two variables represent the unequal relation between two algebraic expressions that includes two distinct variables. Hence, the symbols used between the expression in two variables will be ‘<’, ‘>’, ‘≤’ or ‘≥’, but we cannot use equal to ‘=’ symbol here.
The examples of linear inequalities in two variables are:
- 3x < 2y + 5
- 8y – 9x > 10
- 9x ≥ 10/y
- x + y ≤ 0
Note: 4x2 + 2x + 5 < 0 is not an example of linear inequality in one variable, because the exponent of x is 2 in the first term. It is a quadratic inequality.
How to Solve Linear Inequalities in Two Variables?
The solution for linear inequalities in two variables is an ordered pair that is true for the inequality statement. Let us say if Ax + By > C is a linear inequality where x and y are two variables, then an ordered pair (x, y) satisfying the statement will be the required solution.
The method of solving linear inequalities in two variables is the same as solving linear equations.
For example, if 2x + 3y > 4 is a linear inequality, then we can check the solution, by putting the values of x and y here.
Let x = 1 and y = 2
Taking LHS, we have;
2 (1) + 3 (2) = 2 + 6 = 8
Since, 8 > 4, therefore, the ordered pair (1, 2) satisfy the inequality 2x + 3y > 4. Hence, (1, 2) is the solution.
We can also put different values of x and y to find different solutions here.
Graphical Solution of Linear Inequalities in Two Variables
The statements involving symbols like ‘<’(less than), ‘>’ (greater than), ‘≤’’(less than or equal to), ‘≥’ (greater than or equal to) and two distinct variables are called linear inequalities in two variables. Let us see here, how to find the solution of such expressions, graphically.
Below are the two examples of linear inequalities shown in the figure. The graph of y > x – 2 and y ≤ 2x + 2 are:
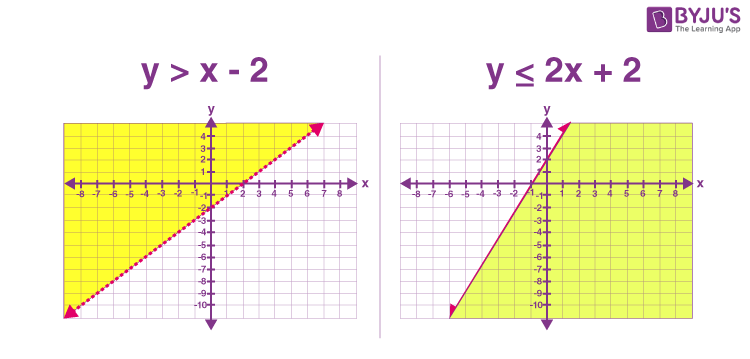
Real-life Examples:
Following example validates the difference between equation and inequality:
Statement 1: The distance between your house and school is exactly 4.5 kilometres,
The mathematical expression of the above statement is,
x = 4.5 km, where ‘x’ is the distance between house and the school.
Statement 2: The distance between your house and the school is at least 4.5 kilometers.
Here, the distance can be 4.5 km or more than that. Therefore the mathematical expression for the above statement is,
x ≥ 4.5 km, where ‘x’ is a variable that is equal to the distance between the house and the school.
Important Facts
- We can add, subtract, multiply and divide by the same number to solve the inequalities
- While multiplying and dividing by negative number, the inequality sign get reversed
- In graphical solution, the ordered pair outside the shaded portion does not solve the inequality
- Numerical inequalities: If only numbers are involved in the expression, then it is a numerical inequality. Example: 10 > 8, 5 < 7
- Literal inequalities: x < 2, y > 5, z < 10 are the examples for literal inequalities.
- Double inequalities: 5 < 7 < 9 read as 7 less than 9 and greater than 5 is an example of double inequality.
- Strict inequality: Mathematical expressions involve only ‘<‘ or ‘>’ are called strict inequalities. Example: 2x + 3 < 6, 2x + 3y > 6
- Slack inequality: Mathematical expressions involve only ‘≤′ or ‘≥’ are called slack inequalities. Example: 2x + 3 ≤ 6, 2x + 3y ≥ 6
Related Articles
- Linear Inequalities
- Solving Linear Inequalities
- Represent Linear Inequalities In One Variable On Number Line
- Linear Equations In Two Variables
- Cross Multiplication- Pair Of Linear Equations In Two Variables
Solved Examples on Linear Inequalities in Two Variables
1.) Classify the following expressions into:
- Linear inequality in one variable.
- Linear inequality in two variables.
- Slack inequality.
5x < 6, 8x + 3y ≤ 5, 2x – 5 < 9 , 2x ≤ 9 , 2x + 3y < 10.
Solution:
| Linear inequality in one variable | Linear inequality in two variables | Slack inequality |
| 5x < 6 | 8x + 3y ≥ 5 | 8x + 3y ≥ 5 |
| 2x – 5 < 9 | 2x + 3y < 10 | 2x ≤ 9 |
| 2x ≤ 9 |
2.) Solve y < 2 graphically.
Solution: Graph of y = 2. So we can show it graphically as given below:

Let us select a point, (0, 0) in the lower half-plane I and putting y = 0 in the given inequality, we see that:
1 × 0 < 2 or 0 < 2 which is true.
Thus, the solution region is the shaded region below the line y = 2.
Hence, every point below the line (excluding all the points on the line) determines the solution of the given inequality.
Linear Inequalities in Two Variables Word Problem
In an experiment, a solution of hydrochloric acid is to be kept between 25° and 30° Celsius. What is the range of temperature in degree Fahrenheit if the conversion formula is given by C = 5/9 (F – 32), where C and F represent the temperature in degree Celsius and degree Fahrenheit, respectively.
Solution: As per the question it is given:
25<C<30
Now if we put C = 5/9 (F – 32), we get;
25 < 5/9 (F – 32) < 30
or
9/5 x 25 < F – 32 < 30 x 9/5
45 < F -32< 54
77 < F < 86
Thus, the required range of temperature is between 77° F and 86° F.


Comments