In Maths, cross multiplication method is used to solve linear equation in two variables. This is the simplest method and gives the accurate value of the variables. Cross multiplication is only applicable when we have a pair of linear equations in two variables.
Let us suppose that a1x + b1y + c1 = 0 and a2x + b2x + c2 = 0 are the two equations which has to be solved. By using cross multiplication, we will get the values x and y such as:
| \(x= \frac{b_1~ c_2~-~b_2~ c_1}{b_2 ~a_1~-~b_1~ a_2}\)
\(y =\frac{c_1~ a_2~-~c_2~ a_1}{b_2~ a_1~-~b_1~ a_2}\) Where \(b_2 ~a_1~-~b_1~ a_2~≠~0\) And the final solution is: \(\frac{x}{b_1~ c_2~-~b_2 ~c_1}\) = \(\frac{y}{c_1 ~a_2~-~c_2~ a_1}\) = \(\frac{1}{b_2~ a_1~-~b_1~ a_2}\) |
The solution of the simultaneous linear equation can be divided into two broad categories, Graphical Method and Algebraic method. The algebraic method can be sub-divided into three categories: Substitution method, Elimination method and cross-multiplication method.
Derivation of Cross multiplication method
In general, a pair of linear equations in two variables can be represented as \(a_1 ~x~+~b_1~y~+~c_1\) = \(0\) and \(a_2 ~x~+~b_2~ y~+~c_2\) = \(0\).
For solving pair of linear equations in two variables following steps are followed:
Given a pair of linear equations in two variables;
\(a_1~ x~+~b_1 ~y~+~c_1\) = \(0\) —(1)
\(a_2~ x~+~b_2 ~y~+~c_2\) = \(0\) —(2)
Step i) Equation (1) is multiplied with \(b_2\) and Equation (2) by \(b_1\).
\(b_2 ~a_1~ x~+~b_2~ b_1 ~y~+~b_2~ c_1\) = \(0\) —(3)
\(b_1~ a_2 ~x~+~b_1~ b_2~ y~+~b_1~ c_2\) = \(0\) —(4)
Step ii) Subtracting Equation (4) from (3):
\((b_2~ a_1~-~b_1~ a_2)x~+~(b_2~ b_1~-~b_1~ b_2)y~+~(b_2~ c_1~-~b_1~ c_2)\) = \(0\)
\(⇒(b_2~ a_1~-~b_1 ~a_2)x\) = \(b_1 ~c_2~-~b_2~ c_1\)
\(⇒~x\) = \(\frac{b_1~ c_2~-~b_2~ c_1}{b_2 ~a_1~-~b_1~ a_2}\) , given \(b_2 ~a_1~-~b_1~ a_2~≠~0\)
Step iii) The value of \(x\) obtained as such is substituted either in Equation (1) or Equation (2).Hence, the value of \(y\) obtained is:
\(y\) = \(\frac{c_1~ a_2~-~c_2~ a_1}{b_2~ a_1~-~b_1~ a_2}\)
The solution of the equations is given as:
\(\frac{x}{b_1~ c_2~-~b_2~ c_1}\) = \(\frac{y}{c_1~ a_2~-~c_2~ a_1}\) = \(\frac{1}{b_2 ~a_1~-~b_1~ a_2}\) —(5)
The above method is called is called ‘Cross-Multiplication Method’, as following cross-multiplication technique can be used to simplify the solution and hence will help in memorizing it. To memorize the method of cross multiplication, for solving linear equation in two variables the following diagram is helpful:
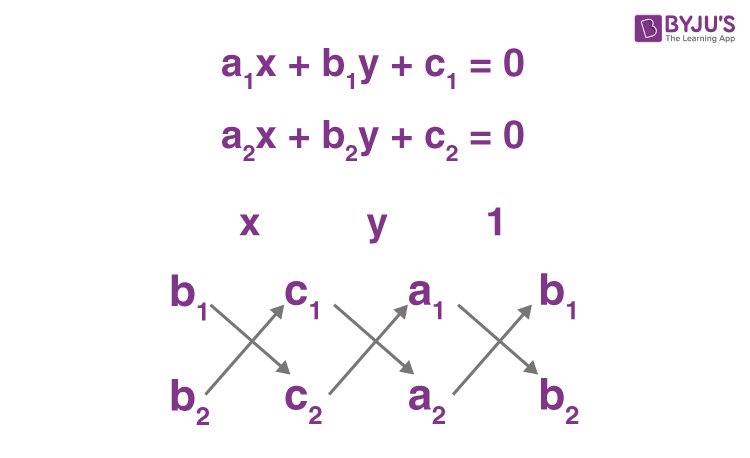
The arrows indicate the multiplication of the values connected through the arrow and then the second product is subtracted from the first. The obtained result is then substituted as the denominator of the variables and 1, as mentioned above the arrow and then the entire values obtained are equated to form equation (5).
\(\frac{x}{b_1~ c_2~-~b_2 ~c_1}\) = \(\frac{y}{c_1 ~a_2~-~c_2~ a_1}\) = \(\frac{1}{b_2~ a_1~-~b_1~ a_2}\)
From here, x and y are evaluated provided that \(a_1~ b_2~-~a_2 ~b_1\) ≠ \(0\). Therefore, this method is called the cross multiplication as depicted.
In such a method, the condition for consistency of pair of linear equation in two variables must be checked, which are as follows:
- If \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\) , then we get a unique solution and the pair of linear equations in two variables are consistent.
- If \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\) , then there exists infinitely many solutions and the pair of lines are coincident and therefore, dependent and consistent.
- If \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\) , then there exists no solution and the pair of linear equations in two variables are said to be inconsistent.
Solved Examples
Consider the following example:
Example 1: Solve the following linear equations using cross multiplication method.
\(3x~-~4y\) = \(2\)
\(y~-~2x\) = \(7\)
Solution: The above equation can be rewritten as:
\(3x~-~4y\) = \(2\)
\(-2x~+~y\) = \(7\)
By method of cross multiplication,
\(\frac{x}{b_1~ c_2~-~b_2~ c_1}\) = \(\frac{y}{c_1 ~a_2~-~c_2~ a_1}\) = \(\frac{1}{b_2 ~a_1~-~b_1~ a_2}\)
Substituting the value in the above equation;
\(\frac{x}{28~+~2}\) = \(\frac{y}{4~+~21}\) = \(\frac{1}{3~-~8}\)
\(⇒~\frac{x}{30}\) = \(\frac{y}{25}\) = \(-\frac{1}{5}\)
\(⇒~x\) = \(-6~,~y\) = \(-5\)
Example 2: Find the value of variables which satisfies the following equation:
2x + 5y = 20 and 3x+6y =12.
Solution: Given,
2x+5y = 20
3x + 6y = 12
By cross multiplication method we know;
\(\frac{x}{b_1~ c_2~-~b_2 ~c_1}\) = \(\frac{y}{c_1 ~a_2~-~c_2~ a_1}\) = \(\frac{1}{b_2~ a_1~-~b_1~ a_2}\)
Hence, by substituting the values in the above equation we get;
x/[(5).(12)-(6).(20)] = y/[(20).(3)-(12).(2)] = 1/[(5).(3)-(6).(2)]
x/(60-120) = y/(60 – 24) = 1/(15-12)
x/(-60) = y/36 = ⅓
Now,
x/-60 = ⅓
x= -20
And
y/36 = ⅓
y = 12
Therefore, x=-20 and y =12 is the point where the given equations intersect.
This is one of the methods for solving such linear equations. To unravel the world of innumerable possibilities and to learn more, please visit www.byjus.com and download BYJU’S -The Learning App.
Frequently Asked Questions – FAQs
What is a cross multiplication method?
Why we use cross multiplication method in linear algebra?
How to find the solution of linear equations in two variables using cross multiplication?
x(b1c2-b2c1) = y/(c1a2-c2a1) = 1/(b2a1-b1a2)
