Square root of 80 = √80 = 8.94427191
Before evaluating the value of the square root of 80, let’s recall the definition and representation of the square root. In mathematics, the square root of a number is a value that gives the original number on multiplication by itself. Suppose a is the square root of b, it is represented as a = √b, or we can express the same equation as a2 = b. Here,’√’ is the radical symbol used to denote the root of numbers. The positive number, when multiplied by itself, represents the square of the number. Thus, the square root of the square of a positive number gives the original number.
In this article, you will learn how to find the square root of 80 in various methods with detailed explanations along with representations and examples.
What is the Square Root of 80?
The square root of 80 is a number that, when multiplied by itself, gives the result as 80. The square root of 80 is symbolically expressed as √80.
Hence, √80 = √(Number × Number)
Let p be the number.
(i.e) √80 = √(p × p)
√80 = √(p)2
So, p2 = 80
We can find the possible value of p, which satisfies the above relation.
Let’s understand how to find the square root of 80.
| Read more: |
Square Root of 80 in Radical Form
To find the radical form of the square root of 80, we should use the prime factorisation of 80. As we know, the prime factorisation of 80 is 2 × 2 × 2 × 2 × 5. Let us write this as 16 × 5.
Here, 16 is a perfect square, whereas 5 is not. Thus, the square root of 80 in radical form is expressed as follows:
√80 = √(2 × 2 × 2 × 2 × 5)
√80 = √(2)2.√(2)2 √3.
√80 = 2 × 2 ×√5
√80 = 4√5.
Therefore, the square root of 80 in radical form is 4√5.
| Square Root of 80 in Radical Form: 4√5. |
Square Root of 80 in Decimal Form
The decimal form of the square root of 80 can be derived from the value of the radical form of the square root of 80.
As we already got the value of root 80 as 4√5.
√80 = 4√5
Now, by substituting the value of the square root of 5 = 2.236, we get;
√80 = 4 × 2.236 = 8.944
| The square root of 80 in Decimal Form: 8.944 |
How to Calculate the Square Root of 80
In mathematics, various methods are available to calculate the value of the square root of 80. They are:
- Repeated subtraction method
- Prime factorisation method
- Long division method
All these methods are explained below with detailed explanations.
Square Root of 80 by Repeated Subtraction Method
In this method, we should subtract the successive odd numbers, i.e. 1, 3, 5, 7,… till we obtain zero, starting from 80 and 1. The number of odd numbers we subtract in this process is treated as the square root of 80.
- 80 – 1 = 79
- 79 – 3 = 76
- 76 – 5 = 71
- 71 – 7 = 64
- 64 – 9 = 55
- 55 – 11 = 44
- 44 – 13 = 31
- 31 -15 = 16
- 16 – 17 = -1
A negative value cannot be possible; also, we didn’t get 0 in the above subtraction but reached almost. Thus, from the above process, we can say that the square root of 80 value is between 8 and 9 as well as it is nearer to 9.
Click here to learn more about the square root of a number by the repeated subtraction method.
Square Root of 80 by Prime Factorisation
In the prime factorisation method, we have to divide the number by prime numbers starting from 2. When it cannot be divided further with 2, divide it with the next prime number, i.e. 3 and continue this process till we get 1.
80 ÷ 2 = 40
Now, divide 40 by 2.
40 ÷ 2 = 20
Continue dividing by 2.
20 ÷ 2 = 10
10 ÷ 2 = 5
5 ÷ 2 = 2.5 (not a factor since the result is not a whole number)
Try dividing 5 by other prime numbers such as 3.
5 ÷ 3 = 1.6667 (not a factor since the result is not a whole number)
5 ÷ 5 = 1
Finally, we received the number 1 in the division process. So that we cannot proceed further. Hence, the prime factorisation of 80 can be written as 2 x 2 × 2 x 2 x 5 or 26 × 5.
Prime factors can also be expressed as given below:
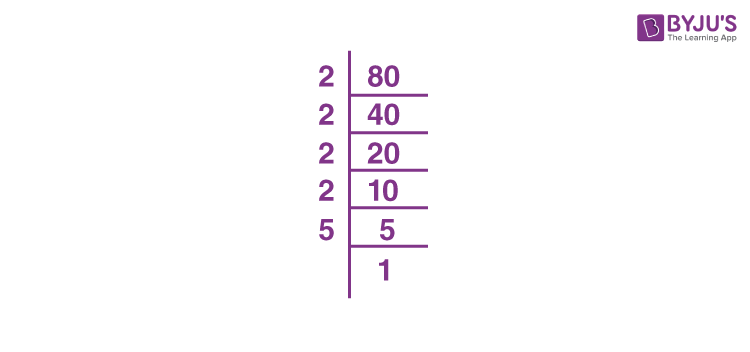
Therefore, the prime factorisation of 80 is 2 × 2 × 2 × 2 × 5.
Let us take these factors as pairs.
That means, 80 = (2 × 2) × (2 × 2) × (5)
Here, we got two pairs of the same numbers, and 5 is left alone.
Now, take the square root on both sides of the above representation.
√80 = √(2 × 2) × (2 × 2) × (5) = 2 × 2 × √5 = 4√5.
Hence, the square root of 80 is equal to 4√5.
Square Root of 80 by Long Division Method
Go through the steps given below to learn how to find the square root of 80 by the long division method:
Step 1: As we know, 80 is not a perfect square; we need to put the decimal point and write pairs of 0s.
Step 2: Find the largest number whose square is less than or equal to the number in the leftmost group, i.e. 80. We know that 82 < 80 < 92, so we can consider 8. Take this number as the divisor and the quotient with the number in the leftmost group as the dividend (80). By dividing the number, we get 16 as the remainder.
Step 3: Now, bring down 00 and add the divisor with the quotient and enter it with a blank on its right. Now, we need to identify the largest possible digit, which will also become the new digit in the quotient so that when the new divisor is multiplied by the new quotient, the product is less than or equal to the dividend. In this case, 169 × 9 = 1521, so we choose the new digit as 9. Then, perform the division and get the remainder.
Step 4: Similar to the previous step, bring down the next pair of 00 and follow the respective procedure. In this case, 1784 × 4 = 7136, so we choose the new digit as 4. Also, get the remainder.
Step 5: Again, bring down the next pair 00 and add the divisor with the quotient and enter it with a blank on its right as we did in the previous steps. In this case, 17884 × 4 = 71536, so we choose the new digit as 4. Finally, get the remainder.
We can repeat this process as many times as required.
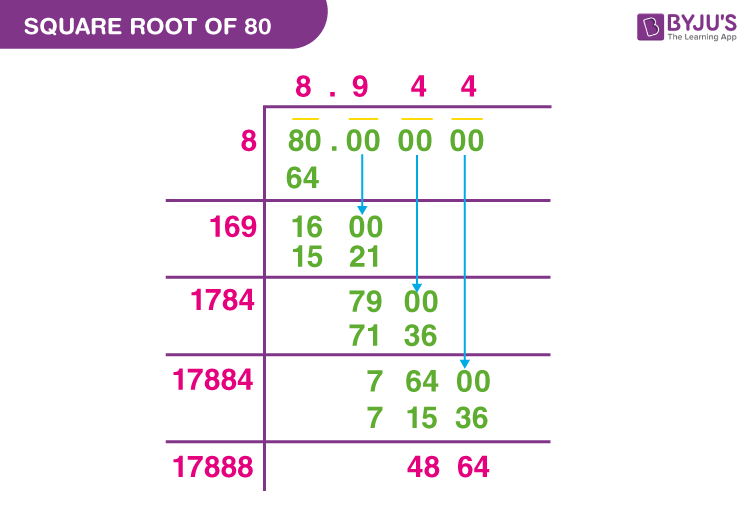
Therefore, the quotient is equal to the square root of the number 80 up to 3 decimal places, i.e. √80 = 8.944.
Get Square Root of More Numbers Here
Video Lessons on Square Roots
Visualising square roots

Finding Square roots

Solved Examples
Example 1:
Simplify: √5 × √80 – 16
Solution:
√5 × √80 – 16
= √5 × 4√5 – 16 {since in radical form √80 = 4√5}
= 4(√5 × √5) – 16
= (4 × 5) – 16
= 20 – 16
= 4
Therefore, √5 × √80 – 16 = 4.
Example 2:
Evaluate: 10 – √80 + √5
Solution:
10 – √80 + √5
= 10 – 4√5 + √5
= 10 + √5(1 – 4)
= 10 – 3√5
We can simplify it further by substituting the √5 value if required.
Frequently Asked Questions on Square Root of 80
What is the value of the square root of 80?
The value of the square root of 80 is 8.944271…
How do you find the value of root 80?
We can find the square root of 80 in multiple ways, such as repeated subtraction, prime factorisation and long division method.
Square root of 80 is rational or irrational?
The square root of 80 is an irrational number as we know that √80 = 8.944271.., not a rational number.
Is 80 a perfect square?
No, 80 is not a perfect square since the square root of 80 is not a whole number but a fraction value, i.e 8.8944…
What is the square of 80?
The square of 80 can be written as 80^2, and it can be calculated as 80^2 = 80 × 80 = 6400. Therefore, the square of 80 is equal to 6400.
Comments