* According to the revised NCERT Syllabus 2023-24 update, this chapter has been removed.
Construction of various shapes, especially in Geometry, is important as students learn various concepts through this topic. It is essential as it has significance in other fields of study too. Moreover, this particular concept is important from an academic perspective as it carries significant marks (28 marks from Unit 4, approximately). Therefore, it is mandatory to learn this concept for exams, and one of the best guides to use for the same is the NCERT Solutions for Class 9 Maths Chapter 11 Constructions Exercise 11.1 and 11.2. Also, NCERT Solutions is held in high regard by many students due to its ease of use and versatile content. This makes it one of the best guides for studies. We have ensured that the conceptual aspects in the chapter are well-articulated in these solutions. Problems are explained with easy examples, and a step-by-step method is used for tougher questions. Besides, content is regularly updated with immediate changes according to the CBSE guidelines (if any).
Download the PDF of NCERT Solutions for Class 9 Maths Chapter 11 – Constructions Exercise 11.2
Access Other Exercise Solutions of Class 9 Chapter 11 – Constructions
Access Answers to NCERT Class 9 Maths Chapter 11 – Constructions Exercise 11.2
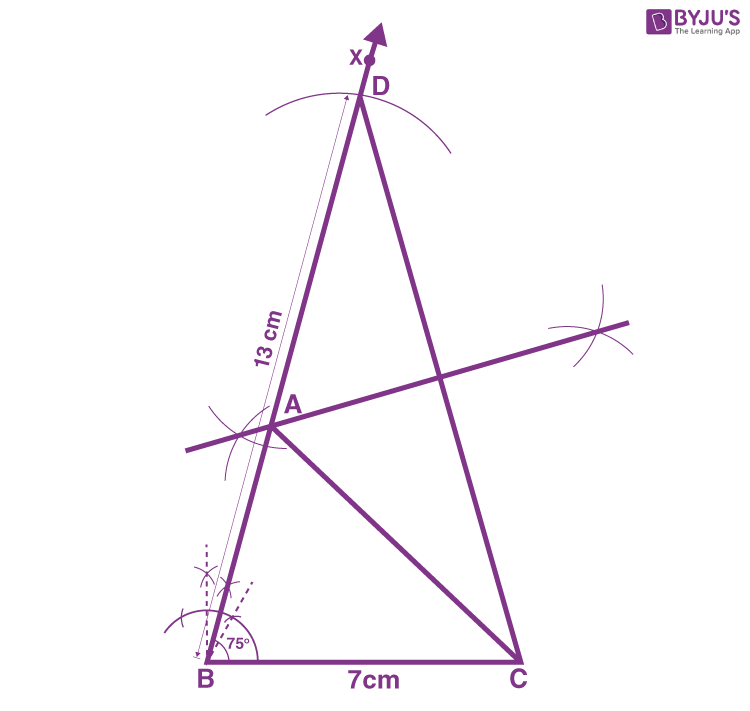
1. Construct a triangle ABC in which BC = 7 cm, ∠B = 75° and AB+AC = 13 cm.
Construction Procedure
The steps to draw the triangle of the given measurement are as follows:
1. Draw a line segment of base BC = 7 cm
2. Measure and draw ∠B = 75° and draw the ray BX
3. Take a compass and measure AB+AC = 13 cm.
4. With B as the centre, draw an arc at the point be D
5. Join DC
6. Now, draw the perpendicular bisector of the line DC, and the intersection point is taken as A
7. Then, join AC
8. Therefore, ABC is the required triangle.
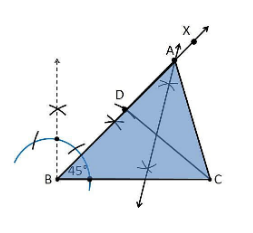
2. Construct a triangle ABC in which BC = 8 cm, ∠B = 45° and AB–AC = 3.5 cm.
Construction Procedure
The steps to draw the triangle of the given measurement are as follows:
1. Draw a line segment of base BC = 8 cm
2. Measure and draw ∠B = 45° and draw the ray BX
3. Take a compass and measure AB-AC = 3.5 cm
4. With B as the centre, draw an arc at point D on the ray BX
5. Join DC
6. Now, draw the perpendicular bisector of the line CD, and the intersection point is taken as A
7. Then, join AC
8. Therefore, ABC is the required triangle.
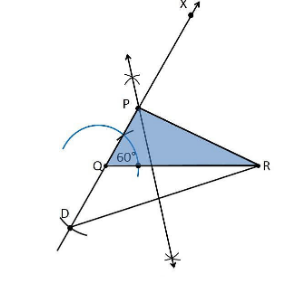
3. Construct a triangle PQR in which QR = 6 cm, ∠Q = 60° and PR–PQ = 2cm.
Construction Procedure
The steps to draw the triangle of the given measurement are as follows:
1. Draw a line segment of base QR = 6 cm
2. Measure and draw ∠Q = 60°, and let the ray be QX
3. Take a compass and measure PR–PQ = 2 cm.
4. Since PR–PQ is negative, QD will be below the line QR.
5. With Q as the centre, draw an arc at the point D on the ray QX
6. Join DR
7. Now, draw the perpendicular bisector of the line DR and the intersection point is taken as P.
8. Then, join PR
9. Therefore, PQR is the required triangle.
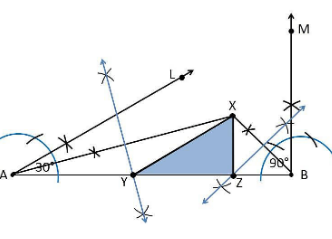
4. Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY+YZ+ZX = 11 cm.
Construction Procedure
The steps to draw the triangle of the given measurement are as follows:
1. Draw a line segment AB which is equal to XY+YZ+ZX = 11 cm.
2. Make an angle ∠LAB = 30° from the point A.
3. Make an angle ∠MBA = 90° from the point B.
4. Bisect ∠LAB and ∠MBA at point X.
5. Now, take the perpendicular bisector of the lines as XA and XB and the intersection point as Y and Z, respectively.
6. Join XY and XZ
7. Therefore, XYZ is the required triangle
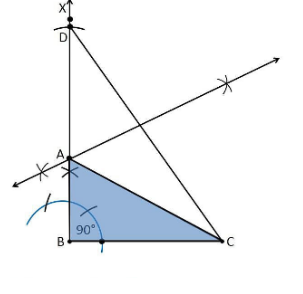
5. Construct a right triangle whose base is 12 cm, and the sum of its hypotenuse and other side is 18 cm.
Construction Procedure:
The steps to draw the triangle of the given measurement are as follows:
1. Draw a line segment of base BC = 12 cm
2. Measure and draw ∠B = 90°, and draw the ray BX
3. Take a compass and measure AB+AC = 18 cm
4. With B as the centre, draw an arc at the point D on the ray BX
5. Join DC
6. Now, draw the perpendicular bisector of the line CD, and the intersection point is taken as A.
7. Then, join AC
8. Therefore, ABC is the required triangle.
Constructions Exercise 11.2 includes 5 practical questions that are based on the concept of geometrical shapes and their process of construction. These exercise questions are crucial from an examination perspective as it helps the students to understand and solve the various questions that might be asked from the topic in the examinations. It also helps students to realise a particular concept’s real-world applications and its significance. Discover various concepts, such as a bisector, perpendicular bisector and more, only on NCERT Solutions for Class 9 Maths.
Key Features of NCERT Solutions for Class 9 Maths Chapter 11 – Constructions Exercise 11.2
- Well-articulated content
- Topics presented in an easy way
- Important formulas are explained
- Comprehensive content
- Content created by experienced teachers
Explore: NCERT Solutions Class 9






Comments