* According to the revised NCERT Syllabus 2023-24 update, this chapter has been removed.
It is important to learn the constructions of various shapes in Geometry as it has applications in various fields of study. Therefore, learning the concept and its applications is crucial from an academic perspective. One of the most efficient ways to learn this elementary concept is by referring to the NCERT Solutions for Class 9 Maths Chapter 11 Constructions Exercise 11.1 and 11.2.
Therefore, NCERT Solutions is the only study guide to consider for learning. Furthermore, the methodologies prescribed in the chapter are presented in an easy-to-understand format. In other words, this means that the instructions provided are unambiguous and precise. Moreover, content is refreshed if any changes are prescribed in the CBSE guidelines.
Download PDF of NCERT Solutions for Class 9 Maths Chapter 11 – Constructions Exercise 11.1
Access Another Exercise Solutions of Class 9 Maths Chapter 11 – Constructions
Access Answers to NCERT Class 9 Chapter 11 – Constructions Exercise 11.1
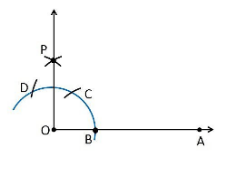
1. Construct an angle of 90° at the initial point of a given ray and justify the construction.
Construction Procedure:
To construct an angle 90°, follow the given steps:
1. Draw a ray OA
2. Take O as a centre with any radius, draw an arc DCB is that cuts OA at B.
3. With B as a centre with the same radius, mark a point C on the arc DCB.
4. With C as a centre and the same radius, mark a point D on the arc DCB.
5. Take C and D as centre, draw two arcs which intersect each other with the same radius at P.
6. Finally, the ray OP is joined which makes an angle 90° with OP is formed.
Justification
To prove ∠POA = 90°
In order to prove this, draw a dotted line from the point O to C and O to D and the angles formed are:
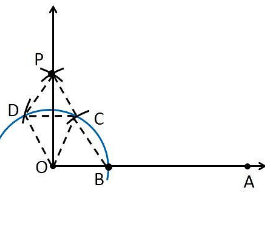
From the construction, it is observed that
OB = BC = OC
Therefore, OBC is an equilateral triangle
So that, ∠BOC = 60°.
Similarly,
OD = DC = OC
Therefore, DOC is an equilateral triangle
So that, ∠DOC = 60°.
From SSS triangle congruence rule
△OBC ≅ OCD
So, ∠BOC = ∠DOC [By C.P.C.T]
Therefore, ∠COP = ½ ∠DOC = ½ (60°).
∠COP = 30°
To find the ∠POA = 90°:
∠POA = ∠BOC+∠COP
∠POA = 60°+30°
∠POA = 90°
Hence, justified.
2. Construct an angle of 45° at the initial point of a given ray and justify the construction.
Construction Procedure:
1. Draw a ray OA
2. Take O as a centre with any radius, draw an arc DCB that cuts OA at B.
3. With B as a centre with the same radius, mark a point C on the arc DCB.
4. With C as a centre and the same radius, mark a point D on the arc DCB.
5. Take C and D as centre, draw two arcs which intersect each other with the same radius at P.
6. Finally, the ray OP is joined which makes an angle 90° with OP is formed.
7. Take B and Q as centre draw the perpendicular bisector which intersects at the point R
8. Draw a line that joins the point O and R
9. So, the angle formed ∠ROA = 45°

Justification
From the construction,
∠POA = 90°
From the perpendicular bisector from the point B and Q, which divides the ∠POA into two halves. So it becomes
∠ROA = ½ ∠POA
∠ROA = (½)×90° = 45°
Hence, justified

Solution:
(i) 30°
Construction Procedure:
1. Draw a ray OA
2. Take O as a centre with any radius, draw an arc BC which cuts OA at B.
3. With B and C as centres, draw two arcs which intersect each other at the point E and the perpendicular bisector is drawn.
4. Thus, ∠EOA is the required angle making 30° with OA.


Construction Procedure:
1. Draw an angle ∠POA = 90°
2. Take O as a centre with any radius, draw an arc BC which cuts OA at B and OP at Q
3. Now, draw the bisector from the point B and Q where it intersects at the point R such that it makes an angle ∠ROA = 45°.
4. Again, ∠ROA is bisected such that ∠TOA is formed which makes an angle of 22.5° with OA

(iii) 15°
Construction Procedure:
1. An angle ∠DOA = 60° is drawn.
2. Take O as centre with any radius, draw an arc BC which cuts OA at B and OD at C
3. Now, draw the bisector from the point B and C where it intersects at the point E such that it makes an angle ∠EOA = 30°.
4. Again, ∠EOA is bisected such that ∠FOA is formed which makes an angle of 15° with OA.
5. Thus, ∠FOA is the required angle making 15° with OA.

4. Construct the following angles and verify by measuring them by a protractor:
(i) 75° (ii) 105° (iii) 135°
Solution:
(i) 75°
Construction Procedure:
1. A ray OA is drawn.
2. With O as centre draw an arc of any radius and intersect at the point B on the ray OA.
3. With B as centre draw an arc C and C as centre draw an arc D.
4. With D and C as centre draw an arc, that intersect at the point P.
5. Join the points O and P
6. The point that arc intersect the ray OP is taken as Q.
7. With Q and C as centre draw an arc, that intersect at the point R.
8. Join the points O and R
9. Thus, ∠AOE is the required angle making 75° with OA.

(ii) 105°
Construction Procedure:
1. A ray OA is drawn.
2. With O as centre draw an arc of any radius and intersect at the point B on the ray OA.
3. With B as centre draw an arc C and C as centre draw an arc D.
4. With D and C as centre draw an arc, that intersect at the point P.
5. Join the points O and P
6. The point that arc intersect the ray OP is taken as Q.
7. With Q and D as centre draw an arc, that intersect at the point R.
8. Join the points O and R
9. Thus, ∠AOR is the required angle making 105° with OA.

(iii) 135°
Construction Procedure:
1. Draw a line AOA‘
2. Draw an arc of any radius that cuts the line AOA‘at the point B and B‘
3. With B as centre, draw an arc of same radius at the point C.
4. With C as centre, draw an arc of same radius at the point D
5. With D and C as centre, draw an arc that intersect at the point P
6. Join OP
7. The point that arc intersect the ray OP is taken as Q and it forms an angle 90°
8. With B‘ and Q as centre, draw an arc that intersects at the point R
9. Thus, ∠AOR is the required angle making 135° with OA.

5. Construct an equilateral triangle, given its side and justify the construction.
Construction Procedure:
1. Let us draw a line segment AB = 4 cm .
2. With A and B as centres, draw two arcs on the line segment AB and note the point as D and E.
3. With D and E as centres, draw the arcs that cuts the previous arc respectively that forms an angle of 60° each.
4. Now, draw the lines from A and B that are extended to meet each other at the point C.
5. Therefore, ABC is the required triangle.

Justification:
From construction, it is observed that
AB = 4 cm, ∠A = 60° and ∠B = 60°
We know that, the sum of the interior angles of a triangle is equal to 180°
∠A+∠B+∠C = 180°
Substitute the values
⇒ 60°+60°+∠C = 180°
⇒ 120°+∠C = 180°
⇒∠C = 60°
While measuring the sides, we get
BC = CA = 4 cm (Sides opposite to equal angles are equal)
AB = BC = CA = 4 cm
∠A = ∠B = ∠C = 60°
Hence, justified.
Chapter 11 – Constructions Exercise 11.1 contains practical questions based on the concept of shapes and their constructions.
Solving exercises is quite important as it helps the students to understand the conceptual basis and solve practical questions on the topic. It also helps students to realise a concept’s real-world implications and their applications.
Explore how to draw a perpendicular bisector and various other problems only on NCERT Solutions For Class 9 Maths. From an examination perspective, it is incredibly useful for last-minute preparations.
Key Features of NCERT Solutions for Class 9 Maths Chapter 11 – Constructions Exercise 11.1
- Content is presented in a well-structured format
- Formulas are explained and highlighted
- Use of easy-to-understand language throughout the content
- Content drafted by knowledgeable teachers
- Complete analysis of important questions
Explore: NCERT Solutions Class 9








Nice Solutions
nice