The vector addition is not as straightforward as the addition of scalars. Vectors have both magnitude and direction, and one cannot simply add two vectors to obtain their sum. To better understand this, let us consider an example of a car travelling 10 miles North and 10 miles South. Here, the total distance travelled is 20 miles, but the displacement is zero. The North and South displacements are each vector quantities, and the opposite directions cause the individual displacements to cancel each other out. In this article, let us explore ways to carry out vector addition and vector subtraction.
| Table of Contents |
Vector Addition: Triangle, Parallelogram and Polygon Law of Vectors
As already discussed, vectors cannot be added algebraically. Following are a few points to remember while adding vectors:
- Vectors are added geometrically and not algebraically.
- Vectors whose resultant have to be calculated behave independently.
- Vector Addition is nothing but finding the resultant of a number of vectors acting on a body.
- Vector Addition is commutative. This means that the resultant vector is independent of the order of vectors.
\(\begin{array}{l}\vec{A} + \vec{B} = \vec{B} + \vec{A}\end{array} \)
Triangle Law of Vector Addition
The vector addition is done based on the triangle law. Let us see what the triangle law of vector addition is:
Suppose there are two vectors, a and b.
Draw a line AB representing vector a with A as the tail and B as the head. Draw another line BC representing vector b with B as the tail and C as the head. Now join the line AC with A as the tail and C as the head. The line AC represents the resultant sum of the vectors a and b.

The line AC represents the resultant sum of the vectors a and b.
The magnitude of vectors a and b is:
Where,
a = magnitude of vector a
b = magnitude of vector b
θ = angle between vector a and b
Let the resultant make an angle of Φ with vector a, then:
Let us understand this using an example. Suppose two vectors have equal magnitude A, and they make an angle θ with each other. Now, to find the magnitude and direction of the resultant, we will use the formulas mentioned above.
Let the magnitude of the resultant vector be B.
Let’s say that the resultant vector makes an angle Ɵ with the first vector.
Or,
Read More: Triangle Law of Vector Addition
Parallelogram Law of Vector Addition
The vector addition may also be understood by the law of parallelogram. The law states, “If two vectors acting simultaneously at a point are represented in magnitude and direction by the two sides of a parallelogram drawn from a point, their resultant is given in magnitude and direction by the diagonal of the parallelogram passing through that point.”
According to this law, if two vectors, P and Q, are represented by two adjacent sides of a parallelogram pointing outwards, as shown in the figure below, then the diagonal drawn through the intersection of the two vectors represent the resultant.

In the Parallelogram Law of Vector Addition, the magnitude of the resultant is given by:
The direction of the resultant vector is determined as follows:
Polygon Law of Vector
According to the polygon law of vector addition, if the number of vectors can be represented in magnitude and direction by the sides of a polygon taken in the same order, then their resultant is represented by magnitude and direction such that the closing side of the polygon is taken in the opposite direction.
Let vector A, vector B, vector C and vector D be the four vectors for which the resultant has to be obtained.
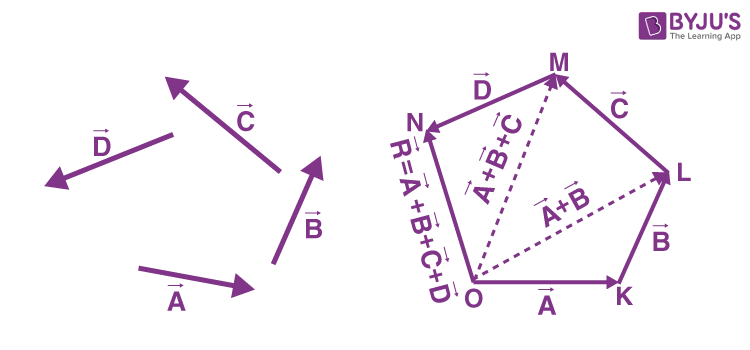
Consider triangle OKL, in which the vectors A and B are represented by sides OK, KL and are taken in the same order. Therefore, from the triangle law of vector addition, we know that the closing side OL is considered in the opposite direction such that it represents the resultant vector OR and KL.
Therefore,
From the triangle law of vector addition, we know that triangle OLM can be expressed as vector OM is the resultant of the vectors OL and LM.
That is,
From eq.1,
Again, applying the triangle law of vector addition to triangle OMN,
From eq.2, we get,
Therefore,
Considering vector ON=vector R, the equation becomes
Click the below video to understand the application of the polygon law of vector addition

Properties of Vector Addition
The vector addition is the sum of multiple (two or more) vectors. Two laws related to the addition of vectors are parallelogram law and triangle law. Similarly, the properties related to vector addition are:
- Associative Property
- Commutative Property
Vector Subtraction
The subtraction of two vectors is similar to addition. Suppose vector a is to be subtracted from vector b.
vector a – vector b can be said as the addition of vectors a and -b. Thus, the addition formula can be applied as:
vector (-b) is nothing but vector b reversed in direction.
Related articles:
| Scalar and Vectors |
| Vectors and Their General Properties |
| Visualizing Unit Vectors |
Frequently Asked Questions – FAQs
What is the maximum and minimum sum of two vectors?
The maximum sum of two vectors is obtained when the two vectors are directed in the same direction. The minimum sum is obtained when the two vectors are directed in the opposite direction.
Is vector addition commutative?
Yes, vector addition is commutative.
Is vector addition applicable to any two vectors?
No, vector addition does not apply to any two vectors. Two vectors are added only when they are of the same type and nature. For instance, two velocity vectors can be added, but one velocity vector and one force vector cannot be added.
State the associative property of vector addition.
The associative property of vector addition states that the sum of the vectors remains the same regardless of the order in which they are arranged.
Can the sum of two vectors have a zero?
Yes, two vectors with equal magnitude and pointing in opposite directions will have the sum equal to zero.
Watch the video and learn about the analytical method of Vector Addition

Stay tuned with BYJU’S to learn more about vectors, vector notation and much more.

Well explained