Band theory of solids is a theoretical model explaining the states of electrons, in solid materials, that can have values of energy only within certain specific ranges. This article examines the band theory of solids in detail.
What is the Band Theory of Solids?
Band theory of solids describes the quantum state that an electron takes inside a metal solid. Every molecule comprises various discrete energy levels. The way electrons behave inside a molecule is well explained through band theory. Band Theory was developed from the knowledge gained during the quantum revolution in science. In 1928, Felix Bloch applied quantum theory to solids.
In atoms, electrons are filled in respective energy orbits following Pauli’s exclusion principle. Two atomic orbitals combine to form a molecular orbit with two distinct energy levels. In solids, 1023 stacked up lines confined in a tiny space would look like a band. Thereby forming an energy continuum called energy bands. Band theory helps to visualise the difference between a conductor, semiconductor, and an insulator by plotting available energies for an electron in a material.
Energy Bands in Solids
In the band theory of solids, there are many energy bands but the following are the three most important energy bands in solids:
- Valence Band
- Conduction Band
- Forbidden Band
Valence band
The energy band that consists of valence electrons energy levels, is known as the valence band. The valence band is present below the conduction band and the electrons of this band are loosely bound to the nucleus of the atom.
Conduction band
The energy band that consists of free electrons energy levels, is known as the conduction band. For electrons to be free, external energy must be applied such that the valence electrons get pushed to the conduction band and become free.
Forbidden band
The energy gap between the valence band and the conduction band is known as the forbidden band which is also known as the forbidden gap. The electrical conductivity of a solid is determined by the forbidden gap and also the classification of the materials as conductors, semiconductors, and insulators.
Energy Band inside an atom
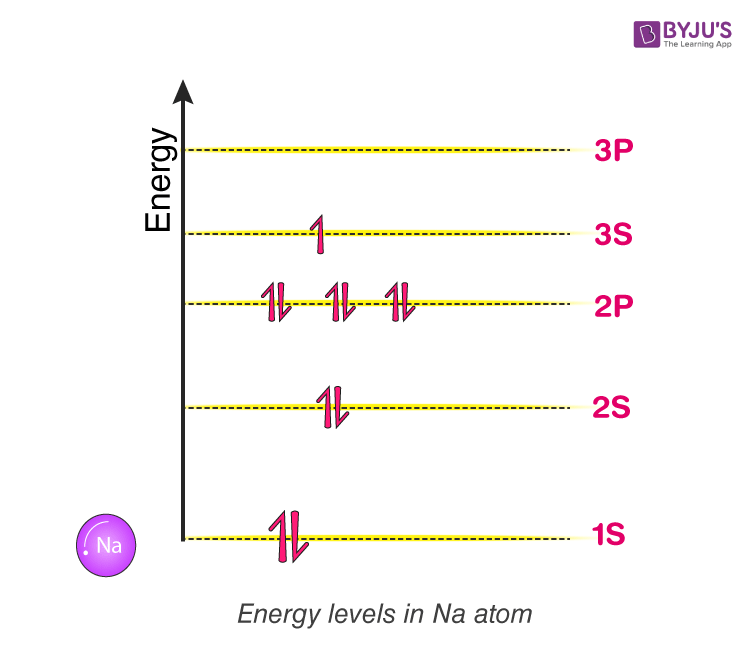
Figure(1)
Consider a Sodium atom. It comprises 11 electrons. They fill up the energy level following Pauli’s exclusion principle. Refer to Figure (1).
Energy levels inside a molecule made up of two atoms
What happens when two sodium atoms are very close to each other, almost forming a molecule? Now each atom cannot have the configuration as it follows as an individual atom. If they do, they will violate Pauli’s exclusion principle and end up with many electrons of the same energy levels.
When two atoms come very close to each other, What is going to happen to this system? The answer is that their respective energy bands will overlap with each other and transform into what we call Molecular orbit. That is, the 1s orbit of individual Sodium atoms combines to form 1s molecular orbital. As two atomic orbitals are overlapping, the molecular orbit ends up having two discrete energy levels. The Lower energy level is called a bonding orbital, and the Higher energy level is called an anti-bonding orbital. This will repeat for all orbits. Refer to figure (2) for the visualisation of energy levels and molecular orbits.
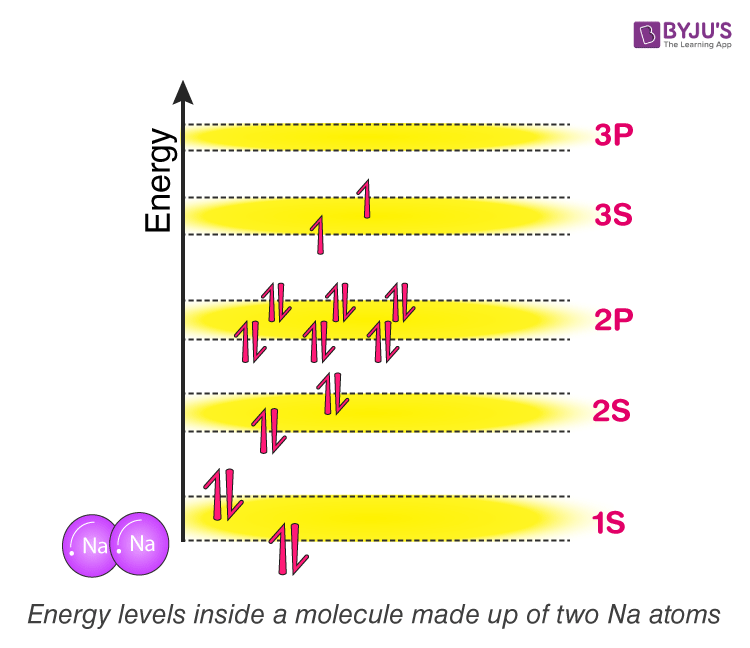
Figure (2)
Energy levels inside a molecule made up of three atoms
Now try to picture what will happen if we add a third sodium atom to the mix? Well, according to the theory we learned just now. Here three atomic orbitals will be overlapping, forming a single molecular orbital with three discrete energy levels. Each molecular orbital here will inherit three energy levels. In general, the more we add atoms, the more energy levels the molecular orbit will have. Refer figure (3)
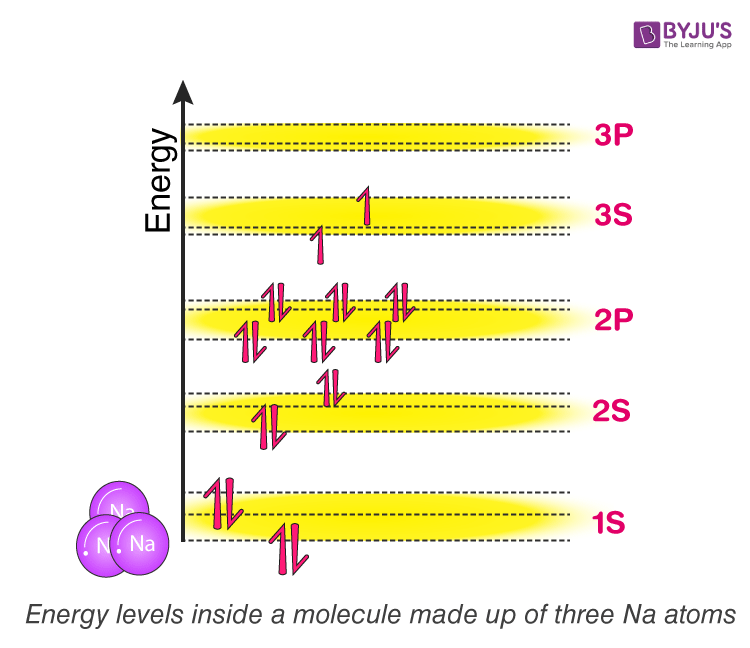
Figure (3)
Energy levels inside a solid made up of Avogadro number of atoms
Eventually, if we have an entire solid made of sodium with something like 1023 atoms packed together, Each molecular orbital of this solid will now have 1023 discrete energy levels. For better understanding purposes, think about drawing 1s orbital of Sodium solid block, draw lower energy level and upper energy level, and in between stack it with 1023 energy levels! Refer to figure(4). The gaps between them will be tiny such that, we no longer can we notice individual energy levels. As a result, It is convenient to think of it as continuous energy or energy continuum. We can call them an energy band instead of a molecular orbit when we think in this way.
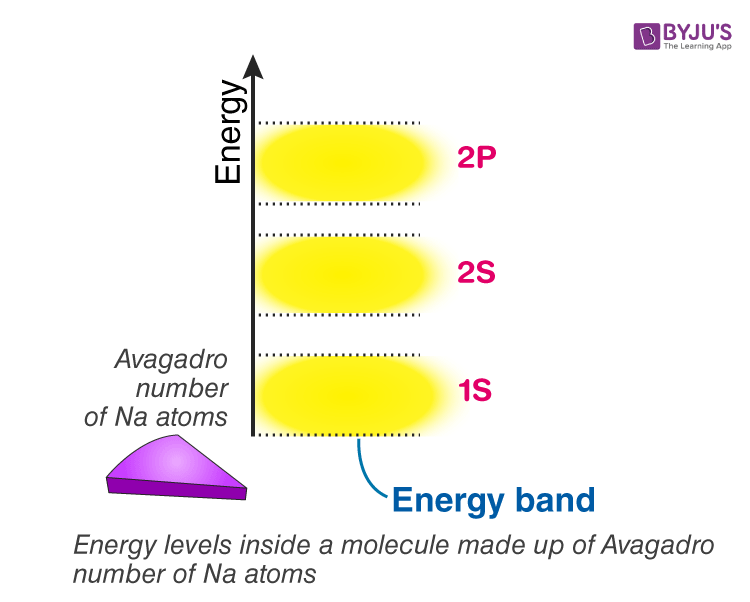
Energy levels inside a solid made up of n-number of atoms
In general, if there are n-number of atoms, there will be n discrete energy levels in each energy band. In such a system of n number of atoms, the molecular orbitals are called energy bands. Single 1s orbital and 2s orbital can fit 2 electrons each. Thus, the total number of electrons a 1s and 2s energy band can fit is 2n. A single 2p level can fit 6 electrons so that a 2p energy band can fit 6n electrons so on and so forth.
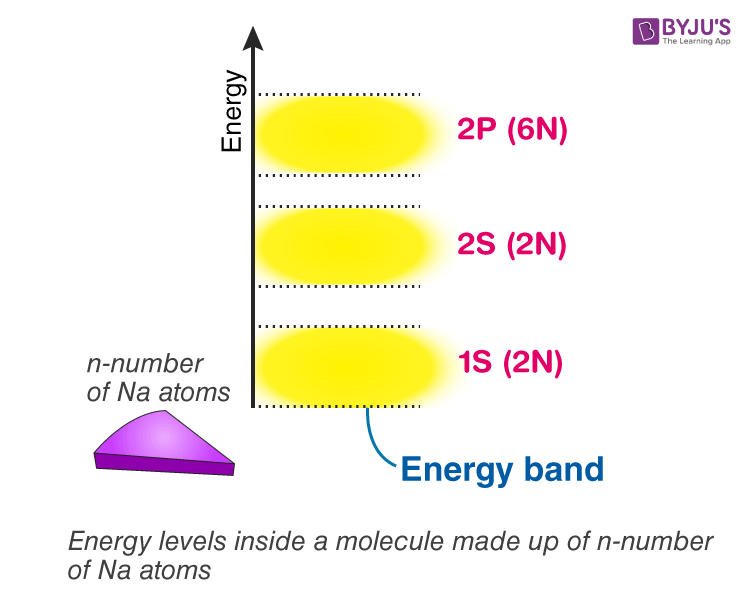
Energy levels inside material of different states of matter
If you have a single atom or if you have gas. In gas, atoms are apart/infinitely apart; we can assume them as single atoms. Here every atom has a discrete energy level, if an electron wants to go from one level to another, it really has to jump as no continuous energy is available(It is similar to steps).
As atoms come close to each other and eventually form a solid, they form an energy continuum, and we name that continuum bands. Within the bands, available energy levels are continuous. Thus, the name of this theory without any surprise is “The band theory of solids.”
Using this theory, we can understand how free electrons are generated and why certain materials readily have free electrons available, making them a conductor and why others don’t?
|
Related Links: |
Frequently Asked Questions – FAQs
What is the band theory of Solids?
Who proposed the band theory of solids?
Which are the three important energy bands in solids?
How are solids classified based on the band theory?
Which band determines the electrical conductivity of a solid?
The Solid State is a chapter that requires a lot of visualisation. The theory is concise, but the students usually struggle with the 3D visualisation of all the lattice points and atoms that fit into them. If you get the visualisation right, this chapter is just a matter of some simple math and formulae! The video discusses some handpicked ones from solid-state.
Stay tuned to BYJU’S for the latest updates. Also, register to “BYJU’S the learning app” to get unlimited physics interactive and engaging video lectures.
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
How the energy bands are formed ?
As discussed in the article, “Two atomic orbitals combine to form a molecular orbit with two distinct energy levels. In solids, 1023 stacked up lines confined in a tiny space would look like a band. Thereby forming an energy continuum called energy bands.”