Magnetic Quantum Number Definition
The magnetic quantum number of an electron is one of the four quantum numbers that state the position of the electron with respect to the nucleus. The other three are-
- Principal quantum number
- Azimuthal quantum number
- Spin quantum number
The magnetic quantum number is the third on the list between spin and azimuthal quantum number. It splits the sub-shells (such as s,p,d,f) into individual orbitals and places the electron in one of them. It defines the orientation in space of a given orbital of particular energy (n) and shape (I).
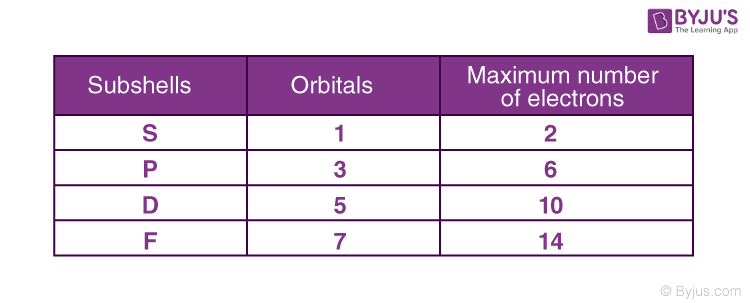
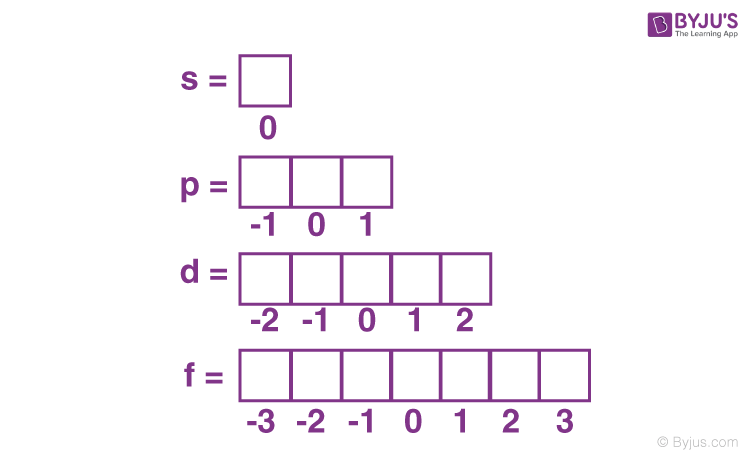
In each sub-shell, the number of orbitals is given as 2+1, where is the azimuthal quantum number. By that process, we can find out the orbital in every sub-shell.
Since the magnetic quantum number is dependent on the azimuthal quantum number, its value ranges from – to +, including 0.
For example, the s sub-shell has only one orbital. The p sub-shell has 3 and d has 5, and so on.
How to find Magnetic Quantum Number?
Quantum numbers in general and magnetic quantum numbers in particular can be derived while solving the Schrodinger equation. However, boundaries or constraints need to be put in place to match the equations with the physical world. The magnetic quantum number can be derived from solving the azimuthal equation of the hydrogen Schrodinger equation.
What does the Magnetic Quantum Number Determine?
The magnetic quantum number primarily determines the number of orbitals and the orientation of orbitals in a given sub-shell. Consequently, it is dependent on the orbital angular momentum quantum number, also known as the azimuthal quantum number.
Among the various proposed models over the years, the Quantum Mechanical Model seems to best fit all properties. Why? Find out all this and more in this intriguing video!


Comments