Polyhedron

In geometry, we may come across different shapes such as one-dimensional, two-dimensional and three-dimensional. Each of these geometric shapes possesses some special properties and applications. A polyhedron is a three-dimensional solid shape with a certain number of faces, edges and vertices. In this article, you will learn polyhedron definition, types, formulas and examples in detail.

Table of Contents:

• Definition
• Shape
• Examples
• Types
• Formula
• Faces edges vertices
• FAQs

Polyhedron Meaning

The word polyhedron has several meanings imperceptibly in geometry and algebraic geometry. In geometry, a polyhedron is just a three-dimensional solid consisting of a group of polygons, ordinarily connected at their edges. In other words, a polyhedron is a three-dimensional variant of the most common polytope, which defines an arbitrary dimension. The plural name of a polyhedron is “polyhedra” or sometimes “polyhedrons”.

The term “polyhedron” is used somewhat differently in algebraic topology. Here, it is defined as a space built from such “building blocks” as line segments, triangles, tetrahedra, and their higher-dimensional analogues by “fixing them together” along with their faces. A polyhedron can be observed as an intersection of half-spaces, whereas a polytope is a bounded polyhedron as shown in the figure below.

Polyhedron Shape

A three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices is called a polyhedron. The word ‘polyhedron’ originates from two Greek words: poly and hedron. Here, “poly” means many and “hedron” indicates surface. The names of polyhedrons are defined by the number of faces it has. The below table shows the names and shapes of different polyhedrons based on the number of faces.

Number of faces	Name of polyhedron	Shape
4	Tetrahedron
5	Pentahedron
6	Hexahedron
7	Heptahedron
8	Octahedron
9	Nonahedron
10	Decahedron
12	Dodecahedron
20	Icosahedron

Polyhedron Examples

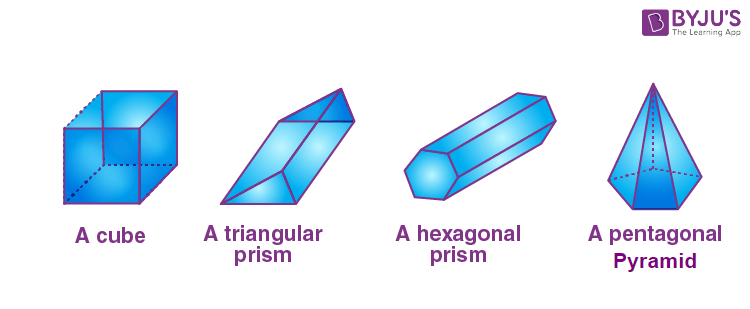
We can observe (as given in the below figure) several polyhedrons in our daily existence such as Rubik’s cube, dice, Buckyball, pyramids and so on.

Diamond is also an example of a polyhedron.

Polyhedron Types

Polyhedrons are classified into two types based on the edges they have. They are:

• Regular polyhedron
• Irregular polyhedron

Let us understand these types of polygons along with the examples here.

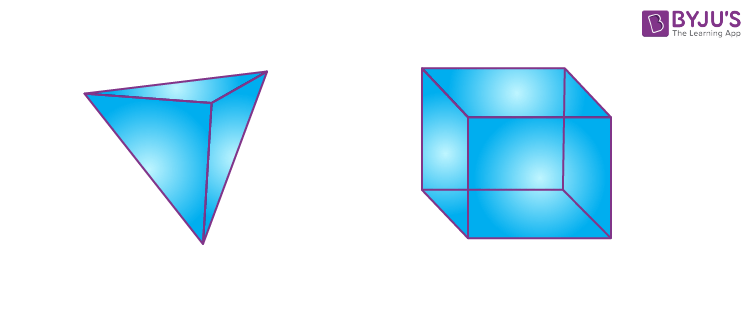
Regular Polyhedron

A regular polyhedron is made up of regular polygons, i.e. all the edges are congruent. These solids are also called platonic solids.

Examples: Triangular pyramid and cube

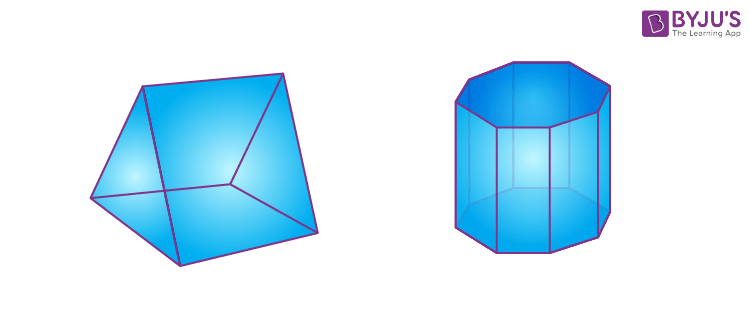
Irregular polyhedron

An irregular polyhedron is formed by polygons having different shapes where all the elements are not the same. In this case, all the sides of an irregular polyhedron are not congruent.

Examples: Triangular prism and Octagonal prism

Polyhedron Formula

If the number of faces and the vertex of a polyhedron are given, we can find the edges using the polyhedron formula. This formula is also known as ‘Euler’s formula’.

F + V = E + 2

Here,

F = Number of faces of the polyhedron

V = Number of vertices of the polyhedron

E = Number of edges of the polyhedron

If we know any two among F, V and E, we can find the third value.

Polyhedron Faces, Edges and Vertices

Every polyhedron has three significant components viz faces edges and vertices.

Faces: The flat surfaces that form a polyhedron are called its faces. These faces are two-dimensional polygons.

Edges: The line segments formed by two regions or two flat surfaces (faces) are known as the edges.

Vertices: The point of intersection of the edges is called the vertex of the polyhedron. A polyhedron can have multiple vertices. These are also known as corners of a polyhedron.

The below figure depicts the faces, edges and vertices of a hexahedron.

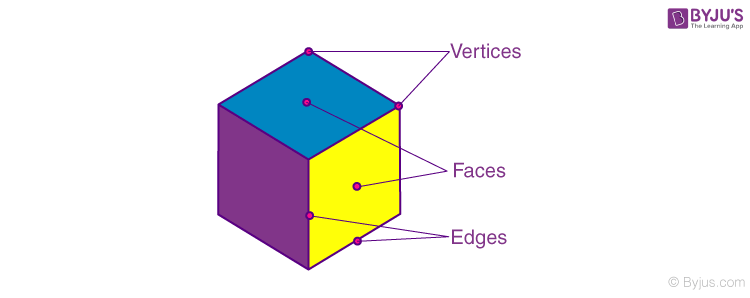
Here,

The number of faces = 6

The number of edges = 12

The number of vertices = 8

Verification using Euler’s formula:

F = 6, E = 12, V = 8

F + V = E + 2

6 + 8 = 12 + 2

14 = 14

In the same way, we can identify the vertices, faces and edges of all the polyhedrons.