In geometry, Scalene Triangle is a triangle that has all its sides of different lengths. It means all the sides of a scalene triangle are unequal and all the three angles are also of different measures. This is one of the three types of triangles, based on sides.
We are going to discuss here its definition, formulas for perimeter and area and its properties. The triangles are defined based on their sides and angles. In geometry, a triangle is a closed two-dimensional plane figure with three sides and three angles and is shown as a three-sided polygon. It has three vertices and three edges.

What is a Scalene Triangle?
A scalene triangle is a triangle in which all three sides are in different lengths, and all three angles are of different measures. However, the sum of all the interior angles is always equal to 180 degrees. Thus, it meets the angle sum property of the triangle.

Classification of Triangles
Based on the sides and the interior angles of a triangle, there are different types of triangle. According to the interior angles of the triangle, it can be classified into three types, namely:
According to the sides of the triangle, the triangle can be classified into three types, namely;
- Scalene Triangle
- Isosceles Triangle
- Equilateral Triangle
Types of Scalene Triangles
A scalene triangle can be classified into three categories:
- Acute-angled scalene triangle: Circumcenter lie inside the triangle
- Obtuse-angled scalene triangle: Circumcenter lie outside the triangle
- Right-angled scalene triangle: Circumcenter is at the midpoint of the hypotenuse
Properties of Scalene Triangle
Some of the important properties of the scalene triangle are as follows:
- It has no equal sides.
- It has no equal angles.
- It has no line of symmetry.
- It has no point symmetry.
- The angles inside this triangle can be an acute, obtuse or right angle.
- If all the angles of the triangle are less than 90 degrees(acute), then the center of the circumscribing circle will lie inside a triangle.
- In a scalene obtuse triangle, the circumcenter will lie outside the triangle.
- A scalene triangle can be an obtuse-angled, acute-angled or right-angled triangle.
Difference Between Scalene, Isosceles and Equilateral Triangles
The basic difference between isosceles, equilateral and scalene triangles are given below in the table. Here, we have compared their angles and sides.
| Scalene Triangle | Isosceles Triangle | Equilateral Triangle |
| All three sides are unequal | Any two sides are equal | All three sides are equal |
| All three angles are different | Angles opposite to equal sides are equal | All three angles equal to 60 degrees |
Formulas of Scalene Triangle
Let us learn the formulas to find the area and perimeter of a triangle that has unequal sides and angles, or we can say the scalene triangle.
Area of a Scalene Triangle

Area = (1/2) x b x h square units
Where,
“b” refers to the base of the triangle
“h” refers to the height of the triangle
If the sides of the triangle are given, then apply Heron’s formula.
Where, s is the semi perimeter of a triangle, which can be found using the formula
s = (a+b+c)/2
Here,
a, b, and c denotes the sides of the triangle
Perimeter of a Scalene Triangle
The perimeter of a triangle is equal to the sum of the length of sides of a triangle and it is given as:
Perimeter = a + b + c units
Example: Consider a given triangle
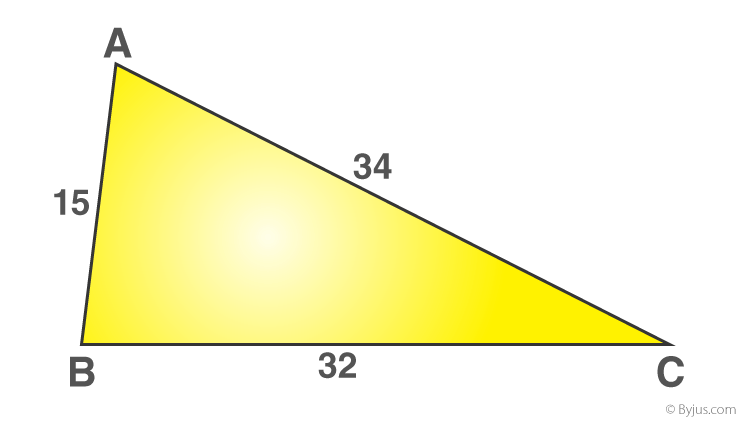
To find the perimeter for the given triangle, add the sides of a triangle
Therefore, perimeter = 15 + 34 + 32 = 81 cm
Video Lesson on Types of Triangles

Solved Examples on Scalene Triangle
Ques.1: Find the area of the scalene triangle ABC with the sides 8 cm, 6 cm and 4 cm.
Solution:
Let a= 8 cm
b = 6 cm
c = 4 cm
If all the sides of a triangle are given, then use Heron’s formula.
Now, find the semi perimeter value
s = (a+b+c)/2
s = (8+6+4)/2
s = 18/2
s = 9
Now substitute the value of S in the area formula,
=√135
=11.6
Therefore, the area of the scalene triangle = 11.6 cm2
Ques.2: If the sides of a triangle are 9cm, 13 cm and 14cm. Find its perimeter.
Solution: Given, length of sides of the triangle are 9cm, 13cm and 14cm.
Perimeter = 9 + 13 + 14 = 36 cms
Practice Questions
Find the area and perimeter of a triangle, for the length of three sides, given below:
- 3cm, 4cm and 5cm
- 8 in., 4in. and 12in
- 3cm, 6cm and 8cm
- 8cm, 11cm and 13cm
Download BYJU’S – The Learning App and learn all the Maths topics from personalised videos.
Frequently Asked Questions on Scalene triangle
What are scalene triangles?
What is the unique property of the scalene triangle?
Does the scalene triangle obey the angle-sum property?
What is a right-scalene triangle?
What is the area and perimeter of scalene triangle?
Perimeter is equal to the sum of its three unequal sides.

Thanks for helping me to solve out my final exam will be great God bless you
Very nice information is provided it helps me a lot for doing my school’s term-1 maths assignment