Exercise 8.1 Solutions: 13 Questions (8 Long Answers, 3 Short, 2 MCQs)
Exercise 8.2 Solutions : 7 Questions(5 Long Answers, 2 MCQs)
Also, explore –
NCERT Solutions for Class 12 Maths Chapter 8
NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals contains solutions for all Exercise 8.3 questions. The textbook questions are answered in a clear and precise manner to help students in their CBSE Board exam preparation. Download the NCERT Maths Solutions of Class 12 from BYJU’S and learn all the concepts effortlessly.
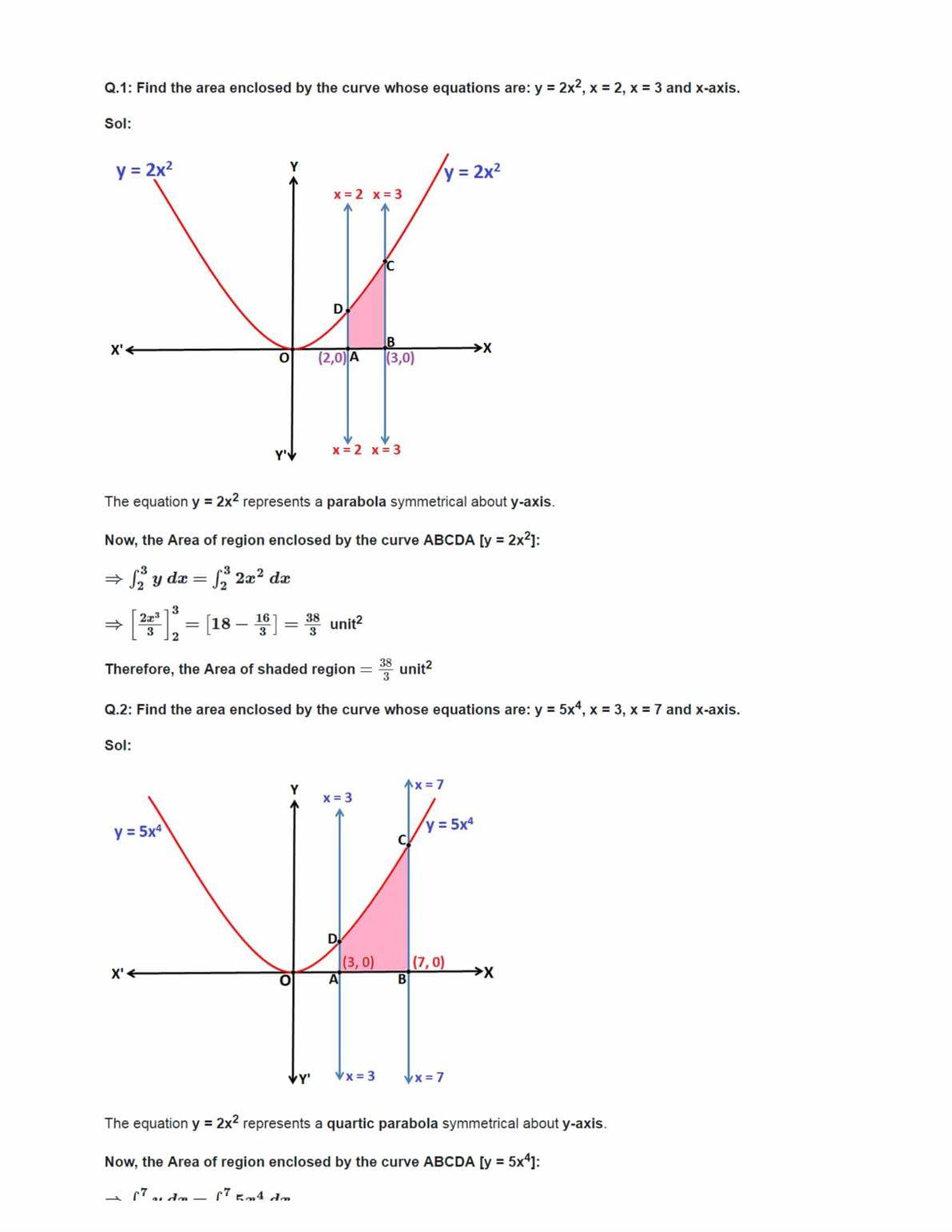




















Exercise 8.1 Solutions: 13 Questions (8 Long Answers, 3 Short, 2 MCQs)
Exercise 8.2 Solutions : 7 Questions(5 Long Answers, 2 MCQs)
Also, explore –
NCERT Solutions for Class 12 Maths Chapter 8
Comments