NCERT Solutions for Class 8 Maths Chapter 14 – Factorisation provides solutions for all the questions listed under the chapter and explains the concepts in simple language. By practising all NCERT questions of Class 8, students will be able to get a good grip on the various concepts and understand the shortcuts thoroughly. It helps in boosting their confidence level, which is essential to ace the exam. NCERT Class 8 Exercise 14.1 solutions make students familiar with the factorisation of numbers as well as algebraic expressions. Download Class 8 Mathematics NCERT Solutions and sharpen your skills.
NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Exercise 14.1
Access Other Exercise Solutions of Class 8 Maths Chapter 14 Factorisation
Exercise 14.2 Solutions: 5 Questions (Short answer type)
Exercise 14.3 Solutions: 5 Questions (Short answer type)
Exercise 14.4 Solutions: 21 Questions (Short answer type)
Access Answers to NCERT Class 8 Maths Chapter 14 Factorisation Exercise 14.1 Page number 220
1. Find the common factors of the given terms.
(i) 12x, 36
(ii) 2y, 22xy
(iii) 14 pq, 28p2q2
(iv) 2x, 3x2, 4
(v) 6 abc, 24ab2, 12a2b
(vi) 16 x3, – 4x2 , 32 x
(vii) 10 pq, 20qr, 30 rp
(viii) 3x2y3 , 10x3y2 , 6x2y2z
Solution:
(i) Factors of 12x and 36
12x = 2×2×3×x
36 = 2×2×3×3
Common factors of 12x and 36 are 2, 2, 3
and , 2×2×3 = 12
(ii) Factors of 2y and 22xy
2y = 2×y
22xy = 2×11×x×y
Common factors of 2y and 22xy are 2, y
and ,2×y = 2y
(iii) Factors of 14pq and 28p2q2
14pq = 2x7xpxq
28p2q2 = 2x2x7xpxpxqxq
Common factors of 14pq and 28 p2q2 are 2, 7 , p , q
and, 2x7xpxq = 14pq
(iv) Factors of 2x, 3x2and 4
2x = 2×x
3x2= 3×x×x
4 = 2×2
Common factors of 2x, 3x2 and 4 is 1.
(v) Factors of 6abc, 24ab2 and 12a2b
6abc = 2×3×a×b×c
24ab2 = 2×2×2×3×a×b×b
12 a2 b = 2×2×3×a×a×b
Common factors of 6abc, 24ab2 and 12a2b are 2, 3, a, b
and, 2×3×a×b = 6ab
(vi) Factors of 16x3 , -4x2and 32x
16 x3 = 2×2×2×2×x×x×x
– 4x2 = -1×2×2×x×x
32x = 2×2×2×2×2×x
Common factors of 16x3 , – 4x2 and 32x are 2,2, x
and, 2×2×x = 4x
(vii) Factors of 10pq, 20qr and 30rp
10 pq = 2×5×p×q
20qr = 2×2×5×q×r
30rp= 2×3×5×r×p
Common factors of 10 pq, 20qr and 30rp are 2, 5
and, 2×5 = 10
(viii) Factors of 3x2y3 , 10x3y2 and 6x2y2z
3x2y3 = 3×x×x×y×y×y
10x3 y2 = 2×5×x×x×x×y×y
6x2y2z = 3×2×x×x×y×y×z
Common factors of 3x2y3, 10x3y2 and 6x2y2z are x2, y2
and, x2×y2 = x2y2
2. Factorise the following expressions
(i) 7x–42
(ii) 6p–12q
(iii) 7a2+ 14a
(iv) -16z+20 z3
(v) 20l2m+30alm
(vi) 5x2y-15xy2
(vii) 10a2-15b2+20c2
(viii) -4a2+4ab–4 ca
(ix) x2yz+xy2z +xyz2
(x) ax2y+bxy2+cxyz
Solution:


(vii) 10a2-15b2+20c2
10a2 = 2×5×a×a
– 15b2 = -1×3×5×b×b
20c2 = 2×2×5×c×c
Common factor of 10 a2 , 15b2 and 20c2 is 5
10a2-15b2+20c2 = 5(2a2-3b2+4c2 )
(viii) – 4a2+4ab-4ca
– 4a2 = -1×2×2×a×a
4ab = 2×2×a×b
– 4ca = -1×2×2×c×a
Common factor of – 4a2 , 4ab , – 4ca are 2, 2, a i.e. 4a
So,
– 4a2+4 ab-4 ca = 4a(-a+b-c)
(ix) x2yz+xy2z+xyz2
x2yz = x×x×y×z
xy2z = x×y×y×z
xyz2 = x×y×z×z
Common factor of x2yz , xy2z and xyz2 are x, y, z i.e. xyz
Now, x2yz+xy2z+xyz2 = xyz(x+y+z)
(x) ax2y+bxy2+cxyz
ax2y = a×x×x×y
bxy2 = b×x×y×y
cxyz = c×x×y×z
Common factor of ax2y ,bxy2 and cxyz is xy
Now, ax2y+bxy2+cxyz = xy(ax+by+cz)
3. Factorise.
(i) x2+xy+8x+8y
(ii) 15xy–6x+5y–2
(iii) ax+bx–ay–by
(iv) 15pq+15+9q+25p
(v) z–7+7xy–xyz
Solution:
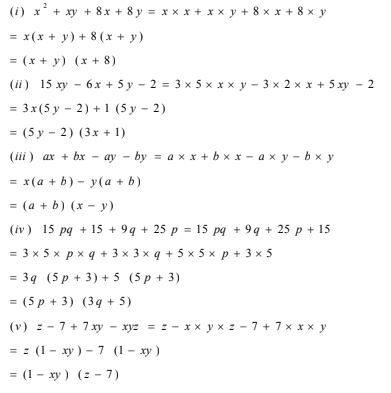
NCERT Class 8 Maths Chapter 14 Factorisation Exercise 14.1 is based on factors of natural numbers, factors of algebraic expressions, methods of common factors, and factorisation by regrouping terms. At the end of this exercise, students will be able to solve any question based on these concepts at their own pace. We have also provided some easy tricks to save your time while working on such problems.
Also, explore –







These extra questions are very helpful in exam time they can understand the concept in better way and these all questions method are very useful and easy
Thank you for these extra questions .😊😊😊