The NCERT Solutions are aimed at helping students master the concepts and acquire comprehensive knowledge about the various types of questions asked in CBSE Class 8 Mathematics Examinations. All the questions are provided with appropriate solutions, which will come in handy in revising the CBSE Class 8 Mathematics syllabus. Solutions for Maths Class 8 are designed by highly knowledgeable subject experts, as per the CBSE curriculum. Class 8 Maths NCERT Solutions are helpful for the students to streamline their last-minute revision. Students can download the PDF and study offline.
NCERT Solutions for Class 8 Maths Chapter 14 Factorisation
Access Answers to NCERT Class 8 Maths Chapter 14 Factorisation
Exercise 14.1 Page No: 208
1. Find the common factors of the given terms.
(i) 12x, 36
(ii) 2y, 22xy
(iii) 14 pq, 28p2q2
(iv) 2x, 3x2, 4
(v) 6 abc, 24ab2, 12a2b
(vi) 16 x3, – 4x2 , 32 x
(vii) 10 pq, 20qr, 30 rp
(viii) 3x2y3 , 10x3y2 , 6x2y2z
Solution:
(i) Factors of 12x and 36
12x = 2×2×3×x
36 = 2×2×3×3
Common factors of 12x and 36 are 2, 2, 3
and , 2×2×3 = 12
(ii) Factors of 2y and 22xy
2y = 2×y
22xy = 2×11×x×y
Common factors of 2y and 22xy are 2, y
and ,2×y = 2y
(iii) Factors of 14pq and 28p2q2
14pq = 2x7xpxq
28p2q2 = 2x2x7xpxpxqxq
Common factors of 14 pq and 28 p2q2 are 2, 7 , p , q
and, 2x7xpxq = 14pq
(iv) Factors of 2x, 3x2and 4
2x = 2×x
3x2= 3×x×x
4 = 2×2
Common factors of 2x, 3x2 and 4 is 1.
(v) Factors of 6abc, 24ab2 and 12a2b
6abc = 2×3×a×b×c
24ab2 = 2×2×2×3×a×b×b
12 a2 b = 2×2×3×a×a×b
Common factors of 6 abc, 24ab2 and 12a2b are 2, 3, a, b
and, 2×3×a×b = 6ab
(vi) Factors of 16x3 , -4x2and 32x
16 x3 = 2×2×2×2×x×x×x
– 4x2 = -1×2×2×x×x
32x = 2×2×2×2×2×x
Common factors of 16 x3 , – 4x2 and 32x are 2,2, x
and, 2×2×x = 4x
(vii) Factors of 10 pq, 20qr and 30rp
10 pq = 2×5×p×q
20qr = 2×2×5×q×r
30rp= 2×3×5×r×p
Common factors of 10 pq, 20qr and 30rp are 2, 5
and, 2×5 = 10
(viii) Factors of 3x2y3 , 10x3y2 and 6x2y2z
3x2y3 = 3×x×x×y×y×y
10x3 y2 = 2×5×x×x×x×y×y
6x2y2z = 3×2×x×x×y×y×z
Common factors of 3x2y3, 10x3y2 and 6x2y2z are x2, y2
and, x2×y2 = x2y2
2.Factorise the following expressions.
(i) 7x–42
(ii) 6p–12q
(iii) 7a2+ 14a
(iv) -16z+20 z3
(v) 20l2m+30alm
(vi) 5x2y-15xy2
(vii) 10a2-15b2+20c2
(viii) -4a2+4ab–4 ca
(ix) x2yz+xy2z +xyz2
(x) ax2y+bxy2+cxyz
Solution:


(vii) 10a2-15b2+20c2
10a2 = 2×5×a×a
– 15b2 = -1×3×5×b×b
20c2 = 2×2×5×c×c
Common factor of 10 a2 , 15b2 and 20c2 is 5
10a2-15b2+20c2 = 5(2a2-3b2+4c2 )
(viii) – 4a2+4ab-4ca
– 4a2 = -1×2×2×a×a
4ab = 2×2×a×b
– 4ca = -1×2×2×c×a
Common factor of – 4a2 , 4ab , – 4ca are 2, 2, a i.e. 4a
So,
– 4a2+4 ab-4 ca = 4a(-a+b-c)
(ix) x2yz+xy2z+xyz2
x2yz = x×x×y×z
xy2z = x×y×y×z
xyz2 = x×y×z×z
Common factor of x2yz , xy2z and xyz2 are x, y, z i.e. xyz
Now, x2yz+xy2z+xyz2 = xyz(x+y+z)
(x) ax2y+bxy2+cxyz
ax2y = a×x×x×y
bxy2 = b×x×y×y
cxyz = c×x×y×z
Common factors of a x2y ,bxy2 and cxyz are xy
Now, ax2y+bxy2+cxyz = xy(ax+by+cz)
3. Factorise.
(i) x2+xy+8x+8y
(ii) 15xy–6x+5y–2
(iii) ax+bx–ay–by
(iv) 15pq+15+9q+25p
(v) z–7+7xy–xyz
Solution:
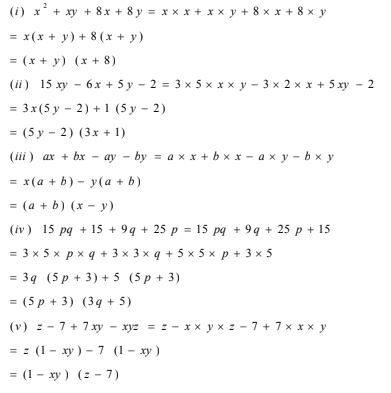
Exercise 14.2 Page No: 223
1. Factorise the following expressions.
(i) a2+8a+16
(ii) p2–10p+25
(iii) 25m2+30m+9
(iv) 49y2+84yz+36z2
(v) 4x2–8x+4
(vi) 121b2–88bc+16c2
(vii) (l+m)2–4lm (Hint: Expand (l+m)2 first)
(viii) a4+2a2b2+b4
Solution:
(i) a2+8a+16
= a2+2×4×a+42
= (a+4)2
Using the identity (x+y)2 = x2+2xy+y2
(ii) p2–10p+25
= p2-2×5×p+52
= (p-5)2
Using the identity (x-y)2 = x2-2xy+y2
(iii) 25m2+30m+9
= (5m)2+2×5m×3+32
= (5m+3)2
Using the identity (x+y)2 = x2+2xy+y2
(iv) 49y2+84yz+36z2
=(7y)2+2×7y×6z+(6z)2
= (7y+6z)2
Using the identity (x+y)2 = x2+2xy+y2
(v) 4x2–8x+4
= (2x)2-2×4x+22
= (2x-2)2
Using the identity (x-y)2 = x2-2xy+y2
(vi) 121b2-88bc+16c2
= (11b)2-2×11b×4c+(4c)2
= (11b-4c)2
Using the identity (x-y)2 = x2-2xy+y2
(vii) (l+m)2-4lm (Hint: Expand (l+m)2 first)
Expand (l+m)2 using the identity (x+y)2 = x2+2xy+y2
(l+m)2-4lm = l2+m2+2lm-4lm
= l2+m2-2lm
= (l-m)2
Using the identity (x-y)2 = x2-2xy+y2
(viii) a4+2a2b2+b4
= (a2)2+2×a2×b2+(b2)2
= (a2+b2)2
Using the identity (x+y)2 = x2+2xy+y2
2. Factorise.
(i) 4p2–9q2
(ii) 63a2–112b2
(iii) 49x2–36
(iv) 16x5–144x3 differ
(v) (l+m)2-(l-m) 2
(vi) 9x2y2–16
(vii) (x2–2xy+y2)–z2
(viii) 25a2–4b2+28bc–49c2
Solution:
(i) 4p2–9q2
= (2p)2-(3q)2
= (2p-3q)(2p+3q)
Using the identity x2-y2 = (x+y)(x-y)
(ii) 63a2–112b2
= 7(9a2 –16b2)
= 7((3a)2–(4b)2)
= 7(3a+4b)(3a-4b)
Using the identity x2-y2 = (x+y)(x-y)
(iii) 49x2–36
= (7x)2 -62
= (7x+6)(7x–6)
Using the identity x2-y2 = (x+y)(x-y)
(iv) 16x5–144x3
= 16x3(x2–9)
= 16x3(x2–9)
= 16x3(x–3)(x+3)
Using the identity x2-y2 = (x+y)(x-y)
(v) (l+m) 2-(l-m) 2
= {(l+m)-(l–m)}{(l +m)+(l–m)}
Using the identity x2-y2 = (x+y)(x-y)
= (l+m–l+m)(l+m+l–m)
= (2m)(2l)
= 4 ml
(vi) 9x2y2–16
= (3xy)2-42
= (3xy–4)(3xy+4)
Using the identity x2-y2 = (x+y)(x-y)
(vii) (x2–2xy+y2)–z2
= (x–y)2–z2
Using the identity (x-y)2 = x2-2xy+y2
= {(x–y)–z}{(x–y)+z}
= (x–y–z)(x–y+z)
Using the identity x2-y2 = (x+y)(x-y)
(viii) 25a2–4b2+28bc–49c2
= 25a2–(4b2-28bc+49c2 )
= (5a)2-{(2b)2-2(2b)(7c)+(7c)2}
= (5a)2-(2b-7c)2
Using the identity x2-y2 = (x+y)(x-y) , we have
= (5a+2b-7c)(5a-2b+7c)
3. Factorise the expressions.
(i) ax2+bx
(ii) 7p2+21q2
(iii) 2x3+2xy2+2xz2
(iv) am2+bm2+bn2+an2
(v) (lm+l)+m+1
(vi) y(y+z)+9(y+z)
(vii) 5y2–20y–8z+2yz
(viii) 10ab+4a+5b+2
(ix)6xy–4y+6–9x
Solution:
(i) ax2+bx = x(ax+b)
(ii) 7p2+21q2 = 7(p2+3q2)
(iii) 2x3+2xy2+2xz2 = 2x(x2+y2+z2)
(iv) am2+bm2+bn2+an2 = m2(a+b)+n2(a+b) = (a+b)(m2+n2)
(v) (lm+l)+m+1 = lm+m+l+1 = m(l+1)+(l+1) = (m+1)(l+1)
(vi) y(y+z)+9(y+z) = (y+9)(y+z)
(vii) 5y2–20y–8z+2yz = 5y(y–4)+2z(y–4) = (y–4)(5y+2z)
(viii) 10ab+4a+5b+2 = 5b(2a+1)+2(2a+1) = (2a+1)(5b+2)
(ix) 6xy–4y+6–9x = 6xy–9x–4y+6 = 3x(2y–3)–2(2y–3) = (2y–3)(3x–2)
4.Factorise.
(i) a4–b4
(ii) p4–81
(iii) x4–(y+z) 4
(iv) x4–(x–z) 4
(v) a4–2a2b2+b4
Solution:
(i) a4–b4
= (a2)2-(b2)2
= (a2-b2) (a2+b2)
= (a – b)(a + b)(a2+b2)
(ii) p4–81
= (p2)2-(9)2
= (p2-9)(p2+9)
= (p2-32)(p2+9)
=(p-3)(p+3)(p2+9)
(iii) x4–(y+z) 4 = (x2)2-[(y+z)2]2
= {x2-(y+z)2}{ x2+(y+z)2}
= {(x –(y+z)(x+(y+z)}{x2+(y+z)2}
= (x–y–z)(x+y+z) {x2+(y+z)2}
(iv) x4–(x–z) 4 = (x2)2-{(x-z)2}2
= {x2-(x-z)2}{x2+(x-z)2}
= { x-(x-z)}{x+(x-z)} {x2+(x-z)2}
= z(2x-z)( x2+x2-2xz+z2)
= z(2x-z)( 2x2-2xz+z2)
(v) a4–2a2b2+b4 = (a2)2-2a2b2+(b2)2
= (a2-b2)2
= ((a–b)(a+b))2
= (a – b)2 (a + b)2
5. Factorise the following expressions.
(i) p2+6p+8
(ii) q2–10q+21
(iii) p2+6p–16
Solution:
(i) p2+6p+8
We observed that 8 = 4×2 and 4+2 = 6
p2+6p+8 can be written as p2+2p+4p+8
Taking Common terms, we get
p2+6p+8 = p2+2p+4p+8 = p(p+2)+4(p+2)
Again, p+2 is common in both the terms.
= (p+2)(p+4)
This implies that p2+6p+8 = (p+2)(p+4)
(ii) q2–10q+21
We observed that 21 = -7×-3 and -7+(-3) = -10
q2–10q+21 = q2–3q-7q+21
= q(q–3)–7(q–3)
= (q–7)(q–3)
This implies that q2–10q+21 = (q–7)(q–3)
(iii) p2+6p–16
We observed that -16 = -2×8 and 8+(-2) = 6
p2+6p–16 = p2–2p+8p–16
= p(p–2)+8(p–2)
= (p+8)(p–2)
So, p2+6p–16 = (p+8)(p–2)
Exercise 14.3 Page No: 227
1. Carry out the following divisions.
(i) 28x4 ÷ 56x
(ii) –36y3 ÷ 9y2
(iii) 66pq2r3 ÷ 11qr2
(iv) 34x3y3z3 ÷ 51xy2z3
(v) 12a8b8 ÷ (– 6a6b4)
Solution:
(i)28x4 = 2×2×7×x×x×x×x
56x = 2×2×2×7×x
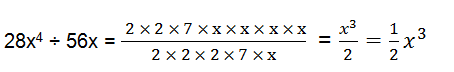
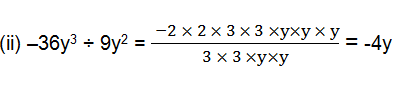
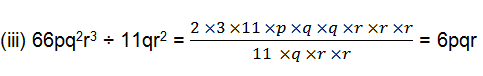
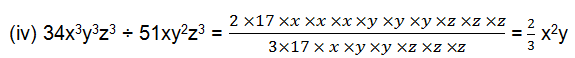
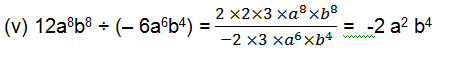
2. Divide the given polynomial by the given monomial.
(i)(5x2–6x) ÷ 3x
(ii)(3y8–4y6+5y4) ÷ y4
(iii) 8(x3y2z2+x2y3z2+x2y2z3)÷ 4x2 y2 z2
(iv)(x3+2x2+3x) ÷2x
(v) (p3q6–p6q3) ÷ p3q3
Solution:
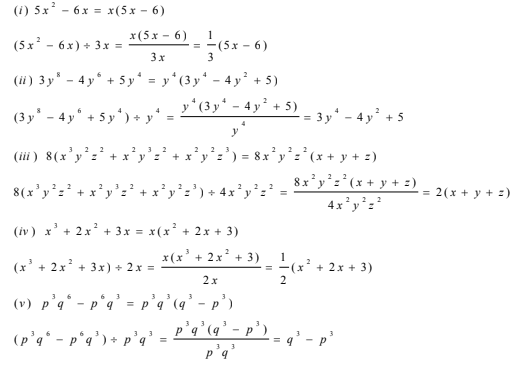
3. Work out the following divisions.
(i) (10x–25) ÷ 5
(ii) (10x–25) ÷ (2x–5)
(iii) 10y(6y+21) ÷ 5(2y+7)
(iv) 9x2y2(3z–24) ÷ 27xy(z–8)
(v) 96abc(3a–12)(5b–30) ÷ 144(a–4)(b–6)
Solution:
(i) (10x–25) ÷ 5 = 5(2x-5)/5 = 2x-5
(ii) (10x–25) ÷ (2x–5) = 5(2x-5)/( 2x-5) = 5
(iii) 10y(6y+21) ÷ 5(2y+7) = 10y×3(2y+7)/5(2y+7) = 6y
(iv) 9x2y2(3z–24) ÷ 27xy(z–8) = 9x2y2×3(z-8)/27xy(z-8) = xy
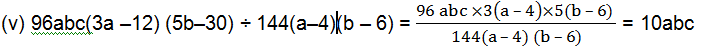
4. Divide as directed.
(i) 5(2x+1)(3x+5)÷ (2x+1)
(ii) 26xy(x+5)(y–4)÷13x(y–4)
(iii) 52pqr(p+q)(q+r)(r+p) ÷ 104pq(q+r)(r+p)
(iv) 20(y+4) (y2+5y+3) ÷ 5(y+4)
(v) x(x+1) (x+2)(x+3) ÷ x(x+1)
Solution:
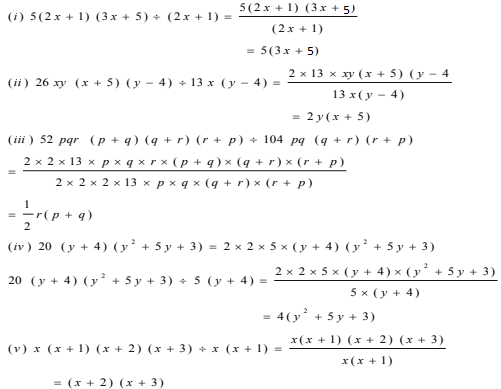
5. Factorise the expressions and divide them as directed.
(i) (y2+7y+10)÷(y+5)
(ii) (m2–14m–32)÷(m+2)
(iii) (5p2–25p+20)÷(p–1)
(iv) 4yz(z2+6z–16)÷2y(z+8)
(v) 5pq(p2–q2)÷2p(p+q)
(vi) 12xy(9x2–16y2)÷4xy(3x+4y)
(vii) 39y3(50y2–98) ÷ 26y2(5y+7)
Solution:
(i) (y2+7y+10)÷(y+5)
First, solve the equation (y2+7y+10)
(y2+7y+10) = y2+2y+5y+10 = y(y+2)+5(y+2) = (y+2)(y+5)
Now, (y2+7y+10)÷(y+5) = (y+2)(y+5)/(y+5) = y+2
(ii) (m2–14m–32)÷ (m+2)
Solve for m2–14m–32, we have
m2–14m–32 = m2+2m-16m–32 = m(m+2)–16(m+2) = (m–16)(m+2)
Now, (m2–14m–32)÷(m+2) = (m–16)(m+2)/(m+2) = m-16
(iii) (5p2–25p+20)÷(p–1)
Step 1: Take 5 common from the equation, 5p2–25p+20, we get
5p2–25p+20 = 5(p2–5p+4)
Step 2: Factorise p2–5p+4
p2–5p+4 = p2–p-4p+4 = (p–1)(p–4)
Step 3: Solve original equation
(5p2–25p+20)÷(p–1) = 5(p–1)(p–4)/(p-1) = 5(p–4)
(iv) 4yz(z2 + 6z–16)÷ 2y(z+8)
Factorising z2+6z–16,
z2+6z–16 = z2-2z+8z–16 = (z–2)(z+8)
Now, 4yz(z2+6z–16) ÷ 2y(z+8) = 4yz(z–2)(z+8)/2y(z+8) = 2z(z-2)
(v) 5pq(p2–q2) ÷ 2p(p+q)
p2–q2 can be written as (p–q)(p+q) using the identity.
5pq(p2–q2) ÷ 2p(p+q) = 5pq(p–q)(p+q)/2p(p+q) = 5q(p–q)/2
(vi) 12xy(9x2–16y2) ÷ 4xy(3x+4y)
Factorising 9x2–16y2 , we have
9x2–16y2 = (3x)2–(4y)2 = (3x+4y)(3x-4y) using the identity p2–q2 = (p–q)(p+q)
Now, 12xy(9x2–16y2) ÷ 4xy(3x+4y) = 12xy(3x+4y)(3x-4y) /4xy(3x+4y) = 3(3x-4y)
(vii) 39y3(50y2–98) ÷ 26y2(5y+7)
st solve for 50y2–98, we have
50y2–98 = 2(25y2–49) = 2((5y)2–72) = 2(5y–7)(5y+7)
Now, 39y3(50y2–98) ÷ 26y2(5y+7) =
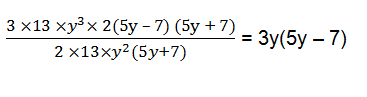
Exercise 14.4 Page No: 228
1. 4(x–5) = 4x–5
Solution:
4(x- 5)= 4x – 20 ≠ 4x – 5 = RHS
The correct statement is 4(x-5) = 4x–20
2. x(3x+2) = 3x2+2
Solution:
LHS = x(3x+2) = 3x2+2x ≠ 3x2+2 = RHS
The correct solution is x(3x+2) = 3x2+2x
3. 2x+3y = 5xy
Solution:
LHS= 2x+3y ≠ R. H. S
The correct statement is 2x+3y = 2x+3 y
4. x+2x+3x = 5x
Solution:
LHS = x+2x+3x = 6x ≠ RHS
The correct statement is x+2x+3x = 6x
5. 5y+2y+y–7y = 0
Solution:
LHS = 5y+2y+y–7y = y ≠ RHS
The correct statement is 5y+2y+y–7y = y
6. 3x+2x = 5x2
Solution:
LHS = 3x+2x = 5x ≠ RHS
The correct statement is 3x+2x = 5x
7. (2x) 2+4(2x)+7 = 2x2+8x+7
Solution:
LHS = (2x) 2+4(2x)+7 = 4x2+8x+7 ≠ RHS
The correct statement is (2x) 2+4(2x)+7 = 4x2+8x+7
8. (2x) 2+5x = 4x+5x = 9x
Solution:
LHS = (2x) 2+5x = 4x2+5x ≠ 9x = RHS
The correct statement is(2x) 2+5x = 4x2+5x
9. (3x + 2) 2 = 3x2+6x+4
Solution:
LHS = (3x+2) 2 = (3x)2+22+2x2x3x = 9x2+4+12x ≠ RHS
The correct statement is (3x + 2) 2 = 9x2+4+12x
10. Substituting x = – 3 in
(a) x2 + 5x + 4 gives (– 3) 2+5(– 3)+4 = 9+2+4 = 15
(b) x2 – 5x + 4 gives (– 3) 2– 5( – 3)+4 = 9–15+4 = – 2
(c) x2 + 5x gives (– 3) 2+5(–3) = – 9–15 = – 24
Solution:
(a) Substituting x = – 3 in x2+5x+4, we have
x2+5x+4 = (– 3) 2+5(– 3)+4 = 9–15+4 = – 2. This is the correct answer.
(b) Substituting x = – 3 in x2–5x+4
x2–5x+4 = (–3) 2–5(– 3)+4 = 9+15+4 = 28. This is the correct answer
(c) Substituting x = – 3 in x2+5x
x2+5x = (– 3) 2+5(–3) = 9–15 = -6. This is the correct answer
11.(y–3)2 = y2–9
Solution:
LHS = (y–3)2 , which is similar to (a–b)2 identity, where (a–b) 2 = a2+b2-2ab
(y – 3)2 = y2+(3) 2–2y×3 = y2+9 –6y ≠ y2 – 9 = RHS
The correct statement is (y–3)2 = y2 + 9 – 6y
12. (z+5) 2 = z2+25
Solution:
LHS = (z+5)2 , which is similar to (a +b)2 identity, where (a+b) 2 = a2+b2+2ab
(z+5) 2 = z2+52+2×5×z = z2+25+10z ≠ z2+25 = RHS
The correct statement is (z+5) 2 = z2+25+10z
13. (2a+3b)(a–b) = 2a2–3b2
Solution:
LHS = (2a+3b)(a–b) = 2a(a–b)+3b(a–b)
= 2a2–2ab+3ab–3b2
= 2a2+ab–3b2
≠ 2a2–3b2 = RHS
The correct statement is (2a +3b)(a –b) = 2a2+ab–3b2
14. (a+4)(a+2) = a2+8
Solution:
LHS = (a+4)(a+2) = a(a+2)+4(a+2)
= a2+2a+4a+8
= a2+6a+8
≠ a2+8 = RHS
The correct statement is (a+4)(a+2) = a2+6a+8
15. (a–4)(a–2) = a2–8
Solution:
LHS = (a–4)(a–2) = a(a–2)–4(a–2)
= a2–2a–4a+8
= a2–6a+8
≠ a2-8 = RHS
The correct statement is (a–4)(a–2) = a2–6a+8
16. 3x2/3x2 = 0
Solution:
LHS = 3x2/3x2 = 1 ≠ 0 = RHS
The correct statement is 3x2/3x2 = 1
17. (3x2+1)/3x2 = 1 + 1 = 2
Solution:
LHS = (3x2+1)/3x2 = (3x2/3x2)+(1/3x2) = 1+(1/3x2) ≠ 2 = RHS
The correct statement is (3x2+1)/3x2 = 1+(1/3x2)
18. 3x/(3x+2) = ½
Solution:
LHS = 3x/(3x+2) ≠ 1/2 = RHS
The correct statement is 3x/(3x+2) = 3x/(3x+2)
19. 3/(4x+3) = 1/4x
Solution:
LHS = 3/(4x+3) ≠ 1/4x
The correct statement is 3/(4x+3) = 3/(4x+3)
20. (4x+5)/4x = 5
Solution:
LHS = (4x+5)/4x = 4x/4x + 5/4x = 1 + 5/4x ≠ 5 = RHS
The correct statement is (4x+5)/4x = 1 + (5/4x)

Solution:
LHS = (7x+5)/5 = (7x/5)+ 5/5 = (7x/5)+1 ≠ 7x = RHS
The correct statement is (7x+5)/5 = (7x/5) +1
| Also Access |
| CBSE Notes for Class 8 Maths Chapter 14 |
NCERT Solutions for Class 8 Maths Chapter 14 Factorisation
Class 8 NCERT exercise-wise questions and answers will help students frame a perfect solution in the Maths exam. These exercise questions can provide students with a topic-wise preparation strategy. Some of the important topics introduced in Class 8 NCERT Solutions Maths are Factorisation, Factors of natural numbers, Factors of algebraic expressions and Division of Algebraic Expressions.
NCERT Solutions for Class 8 Maths Chapter 14 Exercises
Get detailed solutions for all the questions below.
Exercise 14.1 Solutions: 3 Questions (Short answer type)
Exercise 14.2 Solutions: 5 Questions (Short answer type)
Exercise 14.3 Solutions: 5 Questions (Short answer type)
Exercise 14.4 Solutions: 21 Questions (Short answer type)
NCERT Solutions for Class 8 Maths Chapter 14 Factorisation
NCERT Class 8 Maths Chapter 14 deals primarily with the factorisation of numbers and algebraic expressions using algebraic identities. Students will also learn about, Division of Algebraic Expressions, Division of a monomial by another monomial, Division of a polynomial by a monomial and Division of Polynomial by Polynomial.
The main topics covered in this chapter include
| Exercise | Topic |
| 14.1 | Introduction |
| 14.2 | What Is Factorisation? |
| 14.3 | Division of Algebraic Expressions |
| 14.4 | Division of Algebraic Expressions |
| 14.5 | Can You Find the Error? |
Key Features of NCERT Solutions for Class 8 Maths Chapter 14 Factorisation
- These NCERT solutions help students understand the concepts clearly.
- Simple and precise language is used to explain the topics.
- All concepts have been explained in detail.
- Subject experts have consolidated all exercise questions in one place for practice.
- NCERT Solutions are helpful for the preparation of competitive exams.
Disclaimer:
Dropped Topics – 14.5 Can you find the error?
Frequently Asked Questions on NCERT Solutions for Class 8 Maths Chapter 14
Are NCERT Solutions for Class 8 Maths Chapter 14 important for the exam?
How many exercises are there in NCERT Solutions for Class 8 Maths Chapter 14?
What are the main topics covered in the NCERT Solutions for Class 8 Maths Chapter 14?
14.1 – Introduction
14.2 – Definition of Factorisation
14.3 – Division of Algebraic Expressions
14.4 – Division of Algebraic Expressions
14.5 – Can You Find the Error?























Nice aap
It helps in learn
Nice app😄😄😄