NCERT Solutions Class 8 Maths Chapter 11 – Free PDF Download
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration is a very important resource for CBSE students. It helps them get a fair idea of the chapter, specifically, the sort of questions that are possibly asked in the exam and the method of answering them. BYJU’S provides all exercise-wise NCERT Class 8 Maths Solutions to help students prepare for the exams and clear doubts.
Download Exclusively Curated Chapter Notes for Class 8 Maths Chapter – 11 Mensuration
Download Most Important Questions for Class 8 Maths Chapter – 11 Mensuration
The branch of Mathematics that deals with geometric figures and their parameters like length, volume, shape, surface area, lateral surface area, etc., is known as Mensuration. Here, the questions related to the concepts of mensuration are well explained in these NCERT Solutions for Class 8 Maths covering all the important mensuration formulas and properties of different geometric shapes and figures. The problems related to the perimeter and area of other plane closed figures like quadrilaterals are solved by subject experts at BYJU’S.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration
Access Answers of NCERT Class 8 Maths Chapter 11 Mensuration
Exercise 11.1 Page No: 171
1. A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
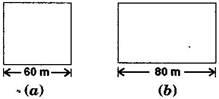
Solution:
Side of a square = 60 m (Given)
And the length of the rectangular field, l = 80 m (Given)
According to the question,
The perimeter of the rectangular field = Perimeter of the square field
2(l+b) = 4×Side (using formulas)
2(80+b) = 4×60
160+2b = 240
b = 40
The breadth of the rectangle is 40 m.
Now, the Area of the Square field
= (side)2
= (60)2 = 3600 m2
And the Area of the Rectangular field
= length×breadth = 80×40
= 3200 m2
Hence, the area of the square field is larger.
2. Mrs.Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of Rs. 55 per m2.
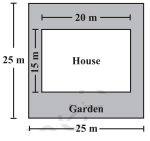
Solution:
Side of the square plot = 25 m
Formula: Area of the square plot = square of the side = (side)2
= (25)2 = 625
Therefore the area of the square plot is 625 m2
Length of the house = 20 m and
The breadth of the house = 15 m
Area of the house = length×breadth
= 20×15 = 300 m2
Area of the garden = Area of the square plot – Area of the house
= 625–300 = 325 m2
∵ The cost of developing the garden per sq. m is Rs. 55
The cost of developing the garden 325 sq. m = Rs. 55×325
= Rs. 17,875
Hence the total cost of developing a garden is around Rs. 17,875.
3. The shape of a garden is rectangular in the middle and semi-circular at the ends as shown in the diagram. Find the area and the perimeter of this garden [Length of rectangle is 20 – (3.5 + 3.5 meters]

Solution::
Given: Total length = 20 m
Diameter of the semi-circle = 7 m
Radius of the semi-circle = 7/2 = 3.5 m
Length of the rectangular field
= 20-(3.5+3.5) = 20-7 = 13 m
Breadth of the rectangular field = 7 m
Area of rectangular field = l×b
= 13×7= 91m2
Area of the two semi-circles = 2×(1/2)×π×r2
= 2×(1/2)×22/7×3.5×3.5
= 38.5 m2
Area of garden = 91+38.5 = 129.5 m2
Now, the perimeter of the two semi-circles = 2πr = 2×(22/7)×3.5 = 22 m
And the perimeter of the garden = 22+13+13
= 48 m. Answer
4. A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? [If required you can split the tiles in whatever way you want to fill up the corners]
Solution:
Given: Base of flooring tile = 24 cm = 0.24 m
Corresponding height of a flooring tile= 10 cm = 0.10 m
Now Area of flooring tile= Base×Altitude
= 0.24×0.10
= 0.024
Area of flooring tile is 0.024m2
Number of tiles required to cover the floor= Area of floor/Area of one tile = 1080/0.024
= 45000 tiles
Hence 45000 tiles are required to cover the floor.
5. An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression C = 2πr ,where r is the radius of the circle.

Solution:
(a) Radius = Diameter/2 = 2.8/2 cm = 1.4 cm
Circumference of semi-circle = πr
= (22/7)×1.4 = 4.4
Circumference of the semi-circle is 4.4 cm
Total distance covered by the ant= Circumference of semi -circle+Diameter
= 4.4+2.8 = 7.2 cm
(b) Diameter of semi-circle = 2.8 cm
Radius = Diameter/2 = 2.8/2 = 1.4 cm
Circumference of semi-circle = r
= (22/7)×1.4 = 4.4 cm
Total distance covered by the ant= 1.5+2.8+1.5+4.4 = 10.2 cm
(c) Diameter of semi-circle = 2.8 cm
Radius = Diameter/2 = 2.8/2
= 1.4 cm
Circumference of semi-circle = π r
= (22/7)×1.4
= 4.4 cm
Total distance covered by the ant = 2+2+4.4 = 8.4 cm
After analyzing the results of three figures, we concluded that for figure (b) food piece, the ant would take a longer round.
Exercise 11.2 Page No: 177
1.The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.

Solution: One parallel side of the trapezium (a) = 1 m
And second side (b) = 1.2 m and
height (h) = 0.8 m
Area of top surface of the table= (½)×(a+b)h
= (½)×(1+1.2)0.8
= (½)×2.2×0.8 = 0.88
Area of top surface of the table is 0.88 m2 .
2. The area of a trapezium is 34 cm2and the length of one of the parallel sides is 10 cm and its height is 4 cm Find the length of the other parallel side.

Solution: Let the length of the other parallel side be b.
Length of one parallel side, a = 10 cm
height, (h) = 4 cm and
Area of a trapezium is 34 cm2
Formula for, Area of trapezium = (1/2)×(a+b)h
34 = ½(10+b)×4
34 = 2×(10+b)
After simplifying, b = 7
Hence another required parallel side is 7 cm.
3. Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.
Solution:

Given: BC = 48 m, CD = 17 m,
AD = 40 m and perimeter = 120 m
∵ Perimeter of trapezium ABCD
= AB+BC+CD+DA
120 = AB+48+17+40
120 = AB = 105
AB = 120–105 = 15 m
Now, Area of the field= (½)×(BC+AD)×AB
= (½)×(48 +40)×15
= (½)×88×15
= 660
Hence, area of the field ABCD is 660m2 .
4. The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.

Solution:

Consider, h1 = 13 m, h2 = 8 m and AC = 24 m
Area of quadrilateral ABCD = Area of triangle ABC+Area of triangle ADC
= ½( bh1)+ ½(bh2)
= ½ ×b(h1+h2)= (½)×24×(13+8)
= (½)×24×21 = 252
Hence, the required area of the field is 252 m2
5. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Solution:
Given: d1 = 7.5 cm and d2 = 12 cm
We know that the area of a rhombus = (½ )×d1×d2
= (½)×7.5×12 = 45
Therefore, the area of the rhombus is 45 cm2 .
6. Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of the diagonals is 8 cm long, find the length of the other diagonal.
Solution: Since a rhombus is also a kind of parallelogram,
The formula for Area of rhombus = Base×Altitude
Putting values, we have
Area of rhombus = 6×4 = 24
Area of rhombus is 24 cm2
Also, Formula for Area of rhombus = (½)×d1d2
After substituting the values, we get
24 = (½)×8×d2
d2 = 6
Hence, the length of the other diagonal is 6 cm.
7. The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2is Rs. 4.
Solution:
Length of one diagonal, d1 = 45 cm and d2= 30 cm
∵ Area of one tile = (½)d1d2
= (½)×45×30 = 675
Area of one tile is 675 cm2
Area of 3000 tiles is
= 675×3000 = 2025000 cm2
= 2025000/10000
= 202.50 m2 [∵ 1m2 = 10000 cm2]
∵ Cost of polishing the floor per sq. meter = 4
Cost of polishing the floor per 202.50 sq. meter = 4×202.50 = 810
Hence the total cost of polishing the floor is Rs. 810.
8. Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.

Solution:
Perpendicular distance (h) = 100 m (Given)
Area of the trapezium-shaped field = 10500 m2 (Given)
Let the side along the road be ‘x’ m and the side along the river = 2x m
Area of the trapezium field = (½)×(a+b)×h
10500 = (½)×(x+2x)×100
10500 = 3x×50
After simplifying, we have x = 70, which means the side along the river is 70 m
Hence, the side along the river = 2x = 2( 70) = 140 m.
9. Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

Solution:
The octagon has eight equal sides, each 5 m. (given)
Divide the octagon as shown in the below figure, 2 trapeziums whose parallel and perpendicular sides are 11 m and 4 m respectively and 3rd one is rectangle having length and breadth 11 m and 5 m respectively.

Now, Area of two trapeziums = 2 [(½)×(a+b)×h]
= 2×(½)×(11+5 )×4
= 4×16 = 64
Area of two trapeziums is 64 m2
Also, Area of rectangle = length×breadth
= 11×5 = 55
Area of rectangle is 55 m2
Total area of octagon = 64+55
= 119 m2
10. There is a pentagonal shaped park as shown in the figure.
For finding its area Jyoti and Kavita divided it in two different ways.

Find the area of this park using both ways. Can you suggest some other way of finding its area?
Solution:
First way: By Jyoti’s diagram,
Area of pentagon = Area of trapezium ABCP + Area of trapezium AEDP
= (½)(AP+BC)×CP+(1/2)×(ED+AP)×DP
= (½)(30+15)×CP+(1/2)×(15+30)×DP
= (½)×(30+15)×(CP+DP)
= (½)×45×CD
= (1/2)×45×15
=337.5 m2
Area of pentagon is 337.5 m2
Second way: By Kavita’s diagram

Here, a perpendicular AM is drawn to BE.
AM = 30–15 = 15 m
Area of pentagon = Area of triangle ABE+Area of square BCDE (from above figure)
= (½)×15×15+(15×15)
= 112.5+225.0
= 337.5
Hence, the total area of pentagon-shaped park = 337.5 m2
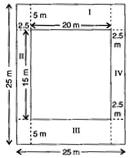
11. Diagram of the adjacent picture frame has outer dimensions = 24 cm×28 cm and inner dimensions 16 cm×20 cm. Find the area of each section of the frame, if the width of each section is same.

Solution:
Divide given figure into 4 parts, as shown below:

Here two of the given figures (I) and (II) are similar in dimensions.
And also, figures (III) and (IV) are similar in dimensions.
Area of figure (I) = Area of trapezium
= (½)×(a+b)×h
= (½)×(28+20)×4
= (½)×48×4 = 96
Area of figure (I) = 96 cm2
Also, Area of figure (II) = 96 cm2
Now, Area of figure (III) = Area of trapezium
= (½)×(a+b)×h
= (½)×(24+16)4
= (½)×40×4 = 80
Area of figure (III) is 80 cm2
Also, Area of figure (IV) = 80 cm2
Exercise 11.3 Page No: 186
1. There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?

Solution:
(a) Given: Length of cuboidal box (l) = 60 cm
Breadth of cuboidal box (b) = 40 cm
Height of cuboidal box (h) = 50 cm
Total surface area of cuboidal box = 2×(lb+bh+hl)
= 2×(60×40+40×50+50×60)
= 2×(2400+2000+3000)
= 14800 cm2
(b) Length of cubical box (l) = 50 cm
Breadth of cubicalbox (b) = 50 cm
Height of cubicalbox (h) = 50 cm
Total surface area of cubical box = 6(side)2
= 6(50×50)
= 6×2500
= 15000
Surface area of the cubical box is 15000 cm2
From the result of (a) and (b), cuboidal box requires the lesser amount of material to make.
2. A suitcase with measures 80 cm x 48 cm x 24 cm is to be covered with a tarpaulin cloth. How many meters of tarpaulin of width 96 cm is required to cover 100 such suitcases?
Solution:
Length of suitcase box, l = 80 cm,
Breadth of suitcase box, b= 48 cm
And Height of cuboidal box , h = 24 cm
Total surface area of suitcase box = 2(lb+bh+hl)
= 2(80×48+48×24+24×80)
= 2 (3840+1152+1920)
= 2×6912
= 13824
Total surface area of suitcase box is 13824 cm2
Area of Tarpaulin cloth = Surface area of suitcase
l×b = 13824
l ×96 = 13824
l = 144
Required tarpaulin for 100 suitcases = 144×100 = 14400 cm = 144 m
Hence tarpaulin cloth required to cover 100 suitcases is 144 m.
3. Find the side of a cube whose surface area is 600cm^2 .
Solution:
Surface area of cube = 600 cm2 (Given)
Formula for surface area of a cube = 6(side)2
Substituting the values, we get
6(side)2 = 600
(side)2 = 100
Or side = ±10
Since side cannot be negative, the measure of each side of a cube is 10 cm
4. Rukshar painted the outside of the cabinet of measure 1 m ×2 m ×1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet?

Solution:
Length of cabinet, l = 2 m, Breadth of cabinet, b = 1 m and Height of cabinet, h = 1.5 m
Area painted = Total surface area of the cabinet – Area of bottom
Total surface area of the cabinet = 2(lb+bh+hl )
= 2(2×1+1×1.5+1.5×2)
= 2(2+1.5+3.0)
= 13 m2
Area of bottom = Length × Breadth
= 2 × 1
= 2 m2
Area painted = 13 – 2 = 11 m2
The required surface area of the cabinet is 11m2.
5. Daniel is paining the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 m^2of area is painted. How many cans of paint will she need to paint the room?
Solution:
Length of wall, l = 15 m, Breadth of wall, b = 10 m and Height of wall, h = 7 m
Total Surface area of classroom = lb+2(bh+hl )
= 15×10+2(10×7+7×15)
= 150+2(70+105)
= 150+350
= 500
Now, Required number of cans = Area of hall/Area of one can
= 500/100 = 5
Therefore, 5 cans are required to paint the room.
6. Describe how the two figures below are alike and how they are different. Which box has larger lateral surface areas?

Solution:
Similarity
Both figures have the same length and the same height
Difference
The first figure has circular bottom and top
The second figure has square bottom and top
The first figure is a cylinder and the second figure is a cube
Diameter of cylinder = 7 cm (Given)
Radius of cylinder, r = 7/2 cm
Height of cylinder, h = 7 cm
Lateral surface area of cylinder = 2πrh
= 2×(22/7)×(7/2)×7 = 154
So, Lateral surface area of cylinder is 154 cm2
Now, lateral surface area of cube = 4 (side)2=4×72 = 4×49 = 196
Lateral surface area of cube is 196 cm2
Hence, the cube has a larger lateral surface area.
7. A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required?
Solution:

Radius of cylindrical tank, r = 7 m
Height of cylindrical tank , h = 3 m
Total surface area of cylindrical tank = 2πr(h+r)
= 2×(22/7)×7(3+7)
= 44×10 = 440
Therefore, 440 m2 metal sheet is required.
8. The lateral surface area of a hollow cylinder is 4224cm2. It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of rectangular sheet?
Solution:
Lateral surface area of hollow cylinder = 4224 cm2
Width of rectangular sheet = 33 cm and say l be the length of the rectangular sheet
Lateral surface area of cylinder = Area of the rectangular sheet
4224 = b × l
4224 = 33 × l
l = 4224/33 = 128 cm
So the length of the rectangular sheet is 128 cm.
Also, Perimeter of rectangular sheet = 2(l+b)
= 2(128+33)
= 322 cm
The perimeter of the rectangular sheet is 322 cm.
9. A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length 1 m.

Solution:
Diameter of road roller, d = 84 cm
Radius of road roller, r = d/2 = 84/2 = 42 cm
Length of road roller, h = 1 m = 100 cm
Formula for Curved surface area of road roller = 2πrh
= 2×(22/7)×42×100 = 26400
Curved surface area of the road roller is 26400 cm2
Again, Area covered by the road roller in 750 revolutions = 26400×750cm2
= 1,98,00,000cm2
= 1980 m2 [∵ 1 m2= 10,000 cm2]
Hence the area of the road is 1980 m2.
10. A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in figure). If the label is placed 2 cm from top and bottom, what is the area of the label?

Solution:
Diameter of the cylindrical container , d = 14 cm
Radius of cylindrical container, r = d/2 = 14/2 = 7 cm
Height of cylindrical container = 20 cm
Height of the label, say h = 20–2–2 (from the figure)
= 16 cm
Curved surface area of label = 2πrh
= 2×(22/7)×7×16
= 704
Hence, the area of the label is 704 cm2.
Exercise 11.4 Page No: 191
1.Given a cylindrical tank, in which situation will you find surface are and in which situation volume.
(a) To find how much it can hold.
(b) Number of cement bags required to plaster it.
(c) To find the number of smaller tanks that can be filled with water from it.
Solution: We find an area when a region is covered by a boundary, such as the outer and inner surface area of a cylinder, a cone, a sphere and surface of wall or floor.
To find the amount of space occupied by an object such as water, milk, coffee, tea, etc., we have to find out the volume of the object.
(a) Volume (b) Surface area (c) Volume
2. Diameter of cylinder A is 7 cm and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area.

Solution:
Yes, we can say that volume of cylinder B is greater, since radius of cylinder B is greater than that of cylinder A.
Find Volume for cylinders A and B
Diameter of cylinder A = 7 cm
Radius of cylinder A = 7/2 cm
And Height of cylinder A = 14 cm
Volume of cylinder A = πr2h
= (22/7 )×(7/2)×(7/2)×14 = 539
Volume of cylinder A is 539 cm3
Now, Diameter of cylinder B = 14 cm
Radius of cylinder B = 14/2 = 7 cm
And Height of cylinder B = 7 cm
Volume of cylinder B = πr2h
= (22/7)×7×7×7 = 1078
Volume of cylinder B is 1078 cm3
Find the surface area of cylinders A and B
Surface area of cylinder A = 2πr(r+h )
= 2 x 22/7 x 7/2 x (7/2 + 14) = 385
Surface area of cylinder A is385 cm2
Surface area of cylinder B = 2πr(r+h)
= 2×(22/7)×7(7+7) = 616
Surface area of cylinder B is 616 cm2
Yes, the cylinder with greater volume also has a greater surface area.
3. Find the height of a cuboid whose base area is 180 cm2 and volume is 900 cm3?
Solution:
Given, Base area of cuboid = 180 cm2 and Volume of cuboid = 900 cm3
We know that, Volume of cuboid = lbh
900 = 180×h (substituting the values)
h= 900/180 = 5
Hence the height of the cuboid is 5 cm.
4. A cuboid is of dimensions 60 cm×54 cm×30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
Solution:
Given, Length of cuboid, l = 60 cm, Breadth of cuboid, b = 54 cm and
Height of cuboid, h = 30 cm
We know that, Volume of cuboid = lbh = 60 ×54×30 = 97200 cm3
And Volume of cube = (Side)3
= 6×6×6 = 216 cm3
Also, the Number of small cubes = volume of cuboid / volume of cube
= 97200/216
= 450
Hence , the required number of cubes is 450.
5. Find the height of the cylinder whose volume if 1.54 m3 and diameter of the base is 140 cm.
Solution:
Given: Volume of cylinder = 1.54 m3and Diameter of cylinder = 140 cm
Radius ( r )= d/2 = 140/2 = 70 cm
Volume of cylinder = πr2h
1.54 = (22/7)×0.7×0.7×h
After simplifying, we get the value of h, which is,
h = (1.54×7)/(22×0.7×0.7)
h = 1
Hence, the height of the cylinder is 1 m.
6. A milk tank is in the form of cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in liters that can be stored in the tank.

Solution:
Given, Radius of cylindrical tank, r = 1.5 m and Height of cylindrical tank, h = 7 m
Volume of cylindrical tank, V = πr2h
= (22/7)×1.5×1.5 ×7
= 49.5 cm3
= 49.5×1000 liters = 49500 liters
[∵ 1 m3= 1000 litres]Hence, the required quantity of milk is 49500 litres.
7. If each edge of a cube is doubled,
(i) how many times will its surface area increase?
(ii) how many times will its volume increase?
Solution:
(i) Let the edge of the cube be “ l” .
Formula for Surface area of the cube, A = 6 l2
When the edge of the cube is doubled, then
Surface area of the cube, say A’ = 6(2l)2 = 6×4l2 = 4(6 l2)
A’ = 4A
Hence, the surface area will increase by four times.
(ii) Volume of a cube, V = l3
When the edge of the cube is doubled, then
Volume of the cube, say V’ = (2l)3 = 8( l3)
V’ = 8×V
Hence, the volume will increase 8 times.
8. Water is pouring into a cuboidal reservoir at the rate of 60 liters per minute. If the volume of reservoir is 108 m^3, find the number of hours it will take to fill the reservoir.
Solution:
Given, the volume of the reservoir = 108 m3
Rate of pouring water into cuboidal reservoir = 60 litres/minute
= 60/1000 m3 per minute
Since 1 liter = (1/1000 )m3
= (60×60)/1000 m3 per hour
Therefore, (60×60)/1000 m3 water filled in reservoir will take = 1 hour
Therefore 1 m3 water filled in reservoir will take = 1000/(60×60) hours
Therefore, 108 m3 water filled in reservoir will take = (108×1000)/(60×60) hours = 30 hours
Answer: It will take 30 hours to fill the reservoir.
| Also Access |
| NCERT Exemplar for Class 8 Maths Chapter 11 |
| CBSE Notes for Class 8 Maths Chapter 11 |
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration
In the previous grade, students learnt about the area and perimeter of closed plane figures such as circles, squares, triangles, rectangles etc. In Class 8 CBSE Maths Chapter 11, students will learn about the surface area and volume of solids such as cube, cuboid and cylinder, area of trapezium, area of quadrilateral, area of special quadrilaterals, area of a polygon, solid shapes, volume and capacity. Students can access this chapter’s NCERT Solutions for Class 8 for solving the exercise problems.
Try NCERT Solutions for Class 8 Maths Chapter 11 problems with answers to understand the concepts, because Mensuration is a topic with real-life applications. All the NCERT Solutions are designed by subject experts according to the latest CBSE Syllabus to help students fetch high marks.
The topics discussed in the chapter revolve around:
1. Area of:
(i) a trapezium = half of the sum of the lengths of parallel sides × perpendicular distance between
them.
(ii) a rhombus = half the product of its diagonals.
2. Surface area of a solid is the sum of the areas of its faces.
3. Surface area of
a cuboid = 2(lb + bh + hl)
a cube = 6l2
a cylinder = 2πr(r + h)
4. Amount of region occupied by a solid is called its volume.
5. Volume of
a cuboid = l × b × h
a cube = l3
a cylinder = πr2h
6. (i) 1 cm3= 1 mL
(ii) 1L = 1000 cm3
(iii) 1 m3 = 1000000 cm3 = 1000L
NCERT Solutions For Class 8 Maths Chapter 11 Exercises:
Get detailed solutions for all the questions listed under the below exercises:
Exercise 11.1 Solutions: 5 Questions (Long answers)
Exercise 11.2 Solutions: 11 Questions (Long answers)
Exercise 11.3 Solutions: 10 Questions (2 Short answers, 8 Long answers)
Exercise 11.4 Solutions: 8 Questions (2 Short answers, 6 Long answers)
Try these NCERT Solutions for Class 8 Maths Chapter 11 about surface area and volume of solids such as cubes, cuboids and cylinders, and the relationship between various geometrical solids. Students will also learn about different mathematical formulas while dealing with mensuration problems.
The main topics covered in this chapter include:
| Exercise | Topic |
| 11.1 | Introduction |
| 11.2 | Let us Recall |
| 11.3 | Area of Trapezium |
| 11.4 | Area of a General Quadrilateral |
| 11.5 | Area of a Polygon |
| 11.6 | Solid Shapes |
| 11.7 | Surface Area of Cube, Cuboid and Cylinder |
| 11.8 | Volume of Cube, Cuboid and Cylinder |
| 11.9 | Volume and Capacity |
Disclaimer:
Dropped Topics – 11.2 Let us Recall, 11.3 Area of Trapezium and 11.4 Area of a General Quadrilateral.
Frequently Asked Questions on NCERT Solutions for Class 8 Maths Chapter 11
How can we score full marks in Class tests of NCERT Solutions for Class 8 Maths Chapter 11?
What are the main concepts covered in NCERT Solutions for Class 8 Maths Chapter 11?
11.1 – Introduction
11.2 – Let us Recall
11.3 – Area of Trapezium
11.4 – Area of a General Quadrilateral
11.5 – Area of a Polygon
11.6 – Solid Shapes
11.7 – Surface Area of Cube, Cuboid and Cylinder
11.8 – Volume of Cube, Cuboid and Cylinder
11.9 – Volume and Capacity.



























Super