NCERT Solutions Class 8 Maths Chapter 8 – Free PDF Download
NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities are developed by subject experts, ensuring the requirements of a CBSE Class 8 student. These NCERT Solutions for Class 8 are to the point and do not confuse students; instead, they help them in reaching a conclusion using the ideal problem-solving method. Solving the exercise questions in the NCERT textbook will offer the students the advantage of preparing themselves adequately well ahead of the final CBSE exams.
Download Exclusively Curated Chapter Notes for Class 8 Maths Chapter – 8 Comparing Quantities
Download Most Important Questions for Class 8 Maths Chapter – 8 Comparing Quantities
BYJU’S NCERT Solutions for Class 8 Maths aims to bring out the best in students by providing skill-building exercises that are apt to their class, strengths and interests. Referring to these solutions will boost confidence among students for taking up CBSE Class 8 Maths exams. The Grade 8 NCERT Solutions are an invaluable aid to students for their exam preparations.
NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities
Access Answers of NCERT Class 8 Maths Chapter 8 – Comparing Quantities
Exercise 8.1 Page No: 119
1. Find the ratio of the following:
(a) Speed of a cycle 15 km per hour to the speed of a scooter 30 km per hour.
(b) 5 m to 10 km
(c) 50 paise to ₹ 5
Solution:
a) Ratio of the speed of the cycle to the speed of the scooter = 15/30 = ½ = 1:2
b) Since 1 km = 1000 m
5m/10 km = 5 m/(10 x 1000)m = 5/10000 = 1/2000 = 1:2000
The required ratio is 1:2000
c) Since, ₹1 = 100 paise
50 paise/₹5 = 50/(5 x 100) = 50/500 = 1/10 = 1:10
The required ratio is 1:10
2. Convert the following ratio to percentages:
a) 3:4
b) 2:3
Solution:
a) 3:4 = ¾ = ¾ x 100% = 0.75 x 100% = 75%
b) 2:3 = 2/3 = 2/3 x 100% = 0.666 x 100% = 66.66% = 66⅔%
3. 72% of 25 students are good in mathematics. How many are not good in mathematics?
Solution:
It’s given that 72% of 25 students are good in mathematics
So, the percentage of students who are not good in mathematics = (100 – 72)%
= 28%
Here, the number of students who are good in mathematics = 72/100 x 25 = 18
Thus, the number of students who are not good in mathematics = 25 – 18 = 7
[Also, 28% of 25 = 28/100 x 25 = 7]Therefore, 7 students are not good in mathematics.
4. A football team won 10 matches out of the total number of matches they played. If their win percentage was 40, then how many matches did they play in all?
Solution:
Let the total number of matches played by the team be x.
Given that the team won 10 matches and the winning percentage of the team was 40%.
⇒ 40/100 × x = 10
40x = 10 × 100
40x = 1000
x = 1000/40
= 100/4
= 25
Therefore, the team played 25 matches.
5. If Chameli had ₹600 left after spending 75% of her money, how much did she have in the beginning?
Solution:
Let the amount of money which Chameli had, in the beginning, be x
Given that, after spending 75% of ₹x, she was left with ₹600
So, (100 – 75)% of x = ₹600
Or, 25% of x = ₹600
25/100 × x = ₹600
x = ₹600 × 4
= ₹2400
Therefore, Chameli had ₹2400 in the beginning.
6. If 60% of people in the city like cricket, 30% like football and the remaining like other games, then what per cent of the people like other games? If the total number of people is 50 lakhs, find the exact number who like each type of game.
Solution:
Percentage of people who like other games = (100 – 60 – 30)%
= (100 – 90)%
= 10%
Total number of people = 50 lakhs
So,
Number of people who like cricket = 60/100 x 50 = 30 lakhs
Number of people who like football = 30/100 x 50 = 15 lakhs
Number of people who like other games = 10/100 x 50 = 5 lakhs
Exercise 8.2 Page No: 125
1. A man got a 10% increase in his salary. If his new salary is ₹1,54,000, find his original salary.
Solution:
Let the original salary be x
Given that, the new salary is ₹1,54,000
Original salary + Increment = New salary
Given that the increment is 10% of the original salary
So, (x + 10/100 × x) = 154000
x + x/10 = 154000
11x/10 = 154000
x = 154000 × 10/11
= 140000
Therefore, the original salary was ₹1,40,000.
2. On Sunday, 845 people went to the zoo. On Monday, only 169 people went. What is the per cent decrease in the number of people visiting the zoo on Monday?
Solution:
Given that on Sunday, 845 people went to the zoo, and on Monday, 169 people went to the zoo.
Decrease in the number of people = 845 – 169 = 676
Thus,
Percentage decrease = (Decrease in the number of people/Number of people who went to the zoo on Sunday) x 100%
= (676/845 x 100)%
= 80%
3. A shopkeeper buys 80 articles for ₹ 2,400 and sells them for a profit of 16%. Find the selling price of one article.
Solution:
Given that the shopkeeper buys 80 articles for ₹ 2,400
Cost of one article = 2400/80 = ₹ 30
Profit percentage = 16%
Profit percentage = Profit/C.P. x 100
16 = Profit/30 x 100
Profit = (16 x 30)/100
= ₹ 4.8
Therefore, the selling price of one article = C.P. + Profit
= ₹ (30 + 4.80)
= ₹ 34.80
4. The cost of an article was ₹ 15,500. ₹ 450 was spent on its repairs. If it is sold for a profit of 15%, find the selling price of the article.
Solution:
The total cost of an article = Cost + Overhead expenses
= ₹15500 + ₹450
= ₹15950
Profit percentage = 15%
Profit percentage = Profit/C.P. x 100
15 = Profit/15950 x 100
Profit = (15 x 15950)/100
= 2392.50
Therefore, the selling price of the article = C.P. + Profit
= ₹(15950 + 2392.50)
= ₹18342.50
5. A VCR and TV were bought for ₹ 8,000 each. The shopkeeper made a loss of 4% on the VCR and a profit of 8% on the TV. Find the gain or loss per cent on the whole transaction.
Solution:
C.P. of a VCR = ₹ 8000
The shopkeeper made a loss of 4 % on VCR
This means if C.P. is ₹ 100, then S.P. is ₹ 96.
When C.P. is ₹ 8000,
S.P. = (96/100 x 8000) = ₹ 7680
C.P. of a TV = ₹ 8000
The shopkeeper made a profit of 8 % on TV.
This means that if C.P. is ₹ 100, then S.P. is ₹ 108.
When C.P. is ₹ 8000,
S.P. = (108/100 x 8000) = ₹ 8640
Total S.P. = ₹ 7680 + ₹ 8640 = ₹ 16320
Total C.P. = ₹ 8000 + ₹ 8000 = ₹ 16000
Since, total S.P.> total C.P. ⇒ profit
Profit = ₹ 16320 − ₹ 16000 = ₹ 320
Profit % on the whole transaction = Profit/Total CP x 100
= 320/16000 x 100
= 2%
Therefore, the shopkeeper had a gain of 2% on the whole transaction.
6. During a sale, a shop offered a discount of 10% on the marked prices of all the items. What would a customer have to pay for a pair of jeans marked at ₹ 1450 and two shirts marked at ₹ 850 each?
Solution:
Total marked price = ₹ (1,450 + 2 × 850)
= ₹ (1,450 +1,700)
= ₹ 3,150
Given that, the discount percentage = 10%
Discount = ₹ (10/100 x 3150) = ₹ 315
Also, Discount = Marked price − Sale price
₹ 315 = ₹ 3150 − Sale price
∴ Sale price = ₹ (3150 − 315)
= ₹ 2835
Therefore, the customer will have to pay ₹ 2,835.
7. A milkman sold two of his buffaloes for ₹ 20,000 each. On one, he made a gain of 5% and on the other, a loss of 10%. Find his overall gain or loss.
(Hint: Find the C.P. of each)
Solution:
S.P. of each buffalo = ₹ 20,000
The milkman made a gain of 5% while selling one buffalo
This means if C.P. is ₹ 100, then S.P. is ₹ 105.
C.P. of one buffalo = 100/105 × 20000
= ₹ 19,047.62
Also, the second buffalo was sold at a loss of 10%
This means if C.P. is ₹ 100, then S.P. is ₹ 90
∴ C.P. of other buffalo = 100/90 × 20000
= ₹ 22222.22
Total C.P. = ₹ 19047.62 + ₹ 22222.22 = ₹ 41269.84
Total S.P. = ₹ 20000 + ₹ 20000 = ₹ 40000
Loss = ₹ 41269.84 − ₹ 40000 = ₹ 1269.84
Therefore, the overall loss of milkman was ₹ 1,269.84
8. The price of a TV is ₹ 13,000. The sales tax charged on it is at the rate of 12%. Find the amount that Vinod will have to pay if he buys it.
Solution:
On ₹ 100, the tax to be paid = ₹ 12
Here, on ₹ 13000, the tax to be paid will be = 12/100 × 13000
= ₹ 1560
Required amount = Cost + Sales Tax
= ₹ 13000 + ₹ 1560
= ₹ 14560
Therefore, Vinod will have to pay ₹ 14,560 for the TV.
9. Arun bought a pair of skates at a sale where the discount given was 20%. If the amount he pays is ₹ 1,600, find the marked price.
Solution:
Let the marked price be x
Discount percent = Discount/Marked Price x 100
20 = Discount/x × 100
Discount = 20/100 × x
= x/5
Also,
Discount = Marked price – Sale price
x/5 = x – ₹ 1600
x – x/5 = 1600
4x/5 = 1600
x = 1600 x 5/4
= 2000
Therefore, the marked price was ₹ 2000.
10. I purchased a hair dryer for ₹ 5,400, including 8% VAT. Find the price before VAT was added.
Solution:
The price includes VAT
So, 8% VAT means that if the price without VAT is ₹ 100,
Then, the price including VAT will be ₹ 108
When price including VAT is ₹ 108, original price = ₹ 100
When price including VAT is ₹ 5400, original price = ₹ (100/108 × 5400)
= ₹ 5000
Therefore, the price of the hair dryer before the addition of VAT was ₹ 5,000.
Exercise 8.3 Page No: 133
1. Calculate the amount and compound interest on
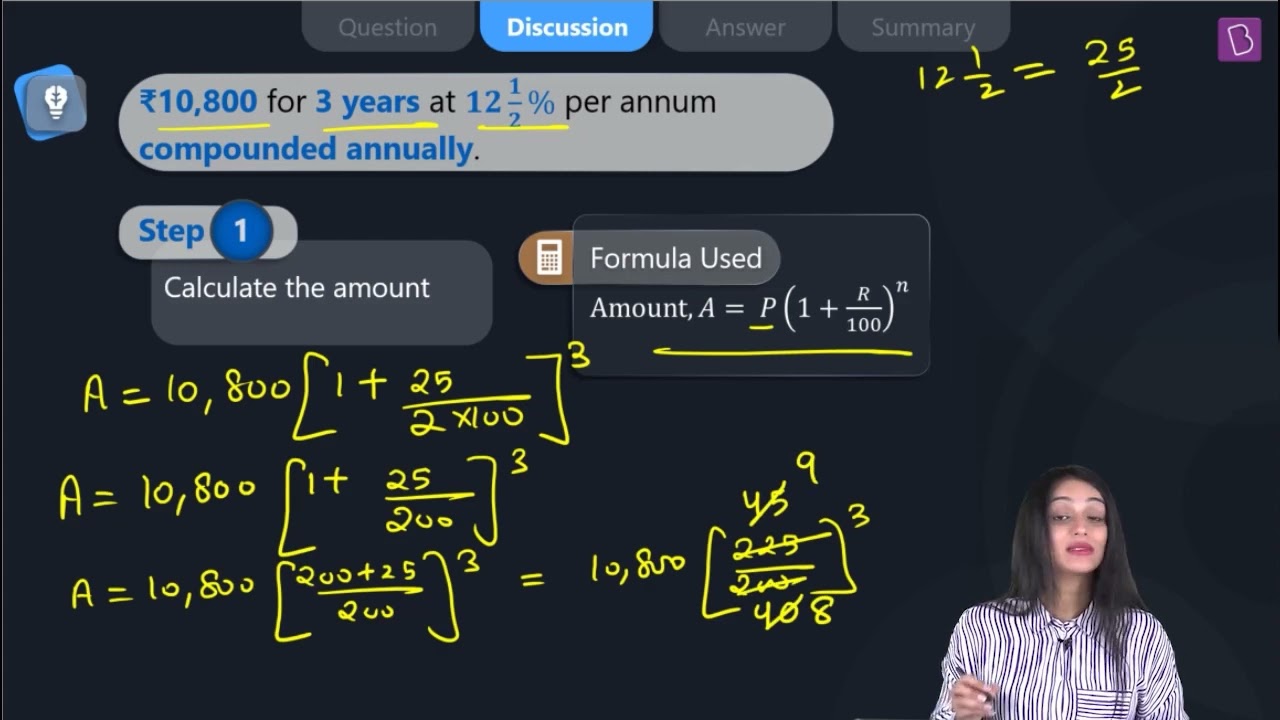
(a) ₹ 10,800 for 3 years at 12½ % per annum compounded annually.
Solution:
Principal (P) = ₹ 10,800
Rate (R) = 12½ % = 25/2 % (annual)
Number of years (n) = 3
Amount (A) = P(1 + R/100)n
= 10800(1 + 25/200)3
= 10800(225/200)3
= 15377.34375
= ₹ 15377.34 (approximately)
C.I. = A – P = ₹ (15377.34 – 10800) = ₹ 4,577.34
(b) ₹ 18000 for 2½ years at 10% per annum compounded annually.
Solution:
Principal (P) = ₹ 18,000
Rate (R) = 10% annual
Number of years (n) = 2½
The amount for 2 years and 6 months can be calculated by calculating the amount for 2 years using the compound interest formula, then calculating the simple interest for 6 months on the amount obtained at the end of 2 years.
First, the amount for 2 years has to be calculated
Amount, A = P(1 + R/100)n
= 18000(1 + 1/10)2
= 18000(11/10)2
= ₹ 21780
By taking ₹ 21780 as principal, the S.I. for the next ½ year will be calculated
S.I. = (21780 x ½ x 10)/100
= ₹ 1089
Hence, the interest for the first 2 years = ₹ (21780 – 18000) = ₹ 3780
And, interest for the next ½ year = ₹ 1089
Total C.I. = ₹ 3780 + ₹ 1089
= ₹ 4,869
Therefore,
Amount, A = P + C.I.
= ₹ 18000 + ₹ 4869
= ₹ 22,869
(c) ₹ 62500 for 1½ years at 8% per annum compounded half yearly.
Solution:
Principal (P) = ₹ 62,500
Rate = 8% per annum or 4% per half-year
Number of years = 1½
There will be 3 half-years in 1½ years
Amount, A = P(1 + R/100)n
= 62500(1 + 4/100)3
= 62500(104/100)3
= 62500(26/25)3
= ₹ 70304
C.I. = A – P = ₹ 70304 – ₹ 62500 = ₹ 7,804
(d) ₹ 8000 for 1 year at 9% per annum compound half yearly.
(You can use the year-by-year calculation using S.I. formula to verify)
Solution:
Principal (P) = ₹ 8000
Rate of interest = 9% per annum or 9/2% per half-year
Number of years = 1 year
There will be 2 half-years in 1 year
Amount, A = P(1 + R/100)n
= 8000(1 + 9/200)2
= 8000(209/200)2
= 8736.20
C.I. = A – P = ₹ 8736.20 – ₹ 8000 = ₹ 736.20
(e) ₹ 10000 for 1 year at 8% per annum compounded half yearly.
Solution:
Principal (P) = ₹ 10,000
Rate = 8% per annum or 4% per half-year
Number of years = 1 year
There are 2 half-years in 1 year
Amount, A = P(1 + R/100)n
= 10000(1 + 4/100)2
= 10000(1 + 1/25)2
= 10000(26/25)2
= ₹ 10816
C.I. = A – P = ₹ 10816 – ₹ 10000 = ₹ 816
2. Kamala borrowed ₹ 26400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?
(Hint: Find A for 2 years with interest compounded yearly and then find S.I. on the 2nd year amount for 4/12 years.)
Solution:
Principal (P) = ₹ 26,400
Rate (R) = 15% per annum
Number of years (n) = 2 4/12
The amount for 2 years and 4 months can be calculated by first calculating the amount for 2 years using the compound interest formula, then calculating the simple interest for 4 months on the amount obtained at the end of 2 years.
First, the amount for 2 years has to be calculated
Amount, A = P(1 + R/100)n
= 26400(1 + 15/100)2
= 26400(1 + 3/20)2
= 26400(23/20)2
= ₹ 34914
By taking ₹ 34,914 as principal, the S.I. for the next 1/3 years will be calculated
S.I. = (34914 × 1/3 x 15)/100 = ₹ 1745.70
Interest for the first two years = ₹ (34914 – 26400) = ₹ 8,514
And interest for the next 1/3 year = ₹ 1,745.70
Total C.I. = ₹ (8514 + ₹ 1745.70) = ₹ 10,259.70
Amount = P + C.I. = ₹ 26400 + ₹ 10259.70 = ₹ 36,659.70
3. Fabina borrows ₹ 12,500 at 12% per annum for 3 years at simple interest, and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest, and by how much?
Solution:
Interest paid by Fabina = (P x R x T)/100
= (12500 x 12 x 3)/100
= 4500
Amount paid by Radha at the end of 3 years = A = P(1 + R/100)n
A = 12500(1 + 10/100)3
= 12500(110/100)3
= ₹ 16637.50
C.I. = A – P = ₹ 16637.50 – ₹ 12500 = ₹ 4,137.50
The interest paid by Fabina is ₹ 4,500 and by Radha is ₹ 4,137.50
Thus, Fabina pays more interest
₹ 4500 − ₹ 4137.50 = ₹ 362.50
Hence, Fabina will have to pay ₹ 362.50 more.
4. I borrowed ₹ 12000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?
Solution:
P = ₹ 12000
R = 6% per annum
T = 2 years
S.I. = (P x R x T)/100
= (12000 x 6 x 2)/100
= ₹ 1440
To find the compound interest, the amount (A) has to be calculated
Amount, A = P(1 + R/100)n
= 12000(1 + 6/100)2
= 12000(106/100)2
= 12000(53/50)2
= ₹ 13483.20
∴ C.I. = A − P
= ₹ 13483.20 − ₹ 12000
= ₹ 1,483.20
C.I. − S.I. = ₹ 1,483.20 − ₹ 1,440
= ₹ 43.20
Therefore, the extra amount to be paid is ₹ 43.20.
5. Vasudevan invested ₹ 60000 at an interest rate of 12% per annum compounded half yearly. What amount would he get
(i) after 6 months?
(ii) after 1 year?
Solution:
(i) P = ₹ 60,000
Rate = 12% per annum = 6% per half-year
n = 6 months = 1 half-year
Amount, A = P(1 + R/100)n
= 60000(1 + 6/100)1
= 60000(106/100)
= 60000(53/50)
= ₹ 63600
(ii) There are 2 half-years in 1 year
So, n = 2
Amount, A = P(1 + R/100)n
= 60000(1 + 6/100)2
= 60000(106/100)2
= 60000(53/50)2
= ₹ 67416
6. Arif took a loan of ₹ 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after 1½ years if the interest is
(i) Compounded annually
(ii) Compounded half yearly
Solution:
(i) P = ₹ 80,000
R = 10% per annum
n = 1½ years
The amount for 1 year and 6 months can be calculated by first calculating the amount for 1 year using the compound interest formula, then calculating the simple interest for 6 months on the amount obtained at the end of 1 year.
First, the amount for 1 year has to be calculated
Amount, A = P(1 + R/100)n
= 80000(1 + 10/100)1
= 80000 x 11/100
= ₹ 88000
By taking ₹ 88,000 as principal, the S.I. for the next ½ year will be calculated as
S.I. = (P x R x T)/100
= (88000 x 10 x ½)/100
= ₹ 4400
Interest for the first year = ₹ 88000 – ₹ 80000 = ₹ 8000
And interest for the next ½ year = ₹ 4,400
Total C.I. = ₹ 8,000 + ₹ 4,400 = ₹ 12,400
A = P + C.I.= ₹ (80000 + 12400)
= ₹ 92,400
(ii) The interest is compounded half yearly
Rate = 10% per annum = 5% per half-year
There will be three half-years in 1½ years
Amount, A = P(1 + R/100)n
= 80000(1 + 5/100)3
= 80000(105/100)3
= ₹ 92610
Thus, the difference between the amounts = ₹ 92,610 – ₹ 92,400 = ₹ 210
7. Maria invested ₹ 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find
(i) The amount credited against her name at the end of the second year
(ii) The interest for the 3rd year
Solution:
(i) P = ₹ 8,000
R = 5% per annum
n = 2 years
Amount, A = P(1 + R/100)n
= 8000(1 + 5/100)2
= 8000(105/100)2
= ₹ 8820
(ii) The interest for the next year, i.e. the third year, has to be calculated. By taking ₹ 8,820 as principal, the S.I. for the next year will be calculated.
S.I. = (P x R x T)/100
= (8820 x 5 x 1)/100
= ₹ 441
8. Find the amount and the compound interest on ₹ 10,000 for 1½ years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually?
Solution:
P = ₹ 10,000
Rate = 10% per annum = 5% per half-year
n = 1½ years
There will 3 half-years in 1½ years
Amount, A = P(1 + R/100)n
= 10000(1 + 5/100)3
= 10000(105/100)3
= ₹ 11576.25
C.I. = A − P
= ₹ 11576.25 − ₹ 10000
= ₹ 1,576.25
The amount for 1 year and 6 months can be calculated by first calculating the amount for 1 year using the compound interest formula, then calculating the simple interest for 6 months on the amount obtained at the end of 1 year.
Amount, A = P(1 + R/100)n
= 10000(1 + 10/100)1
= 10000(110/100)
= ₹ 11000
By taking ₹ 11,000 as the principal, the S.I. for the next ½ year will be calculated as
S.I. = (P x R x T)/100
= (11000 x 10 x ½)/100
= ₹ 550
So, the interest for the first year = ₹ 11000 − ₹ 10000 = ₹ 1,000
Hence, Total compound interest = ₹ 1000 + ₹ 550 = ₹ 1,550
So the difference between two interests = 1576.25 – 1550 = 26.25
Therefore, the interest would be 26.25 more when compounded half yearly than the interest when compounded annually.
9. Find the amount which Ram will get on ₹ 4,096, if he gave it for 18 months at 12½ per annum, interest being compounded half-yearly.
Solution:
P = ₹ 4,096
R = 12½ per annum = 25/2 per annum = 25/4 per half-year
n = 18 months
There will be 3 half-years in 18 months
Therefore, amount A = P(1 + R/100)n
= 4096(1 + 25/(4 x 100))3
= 4096 x (1 + 1/16)3
= 4096 x (17/16)3
= ₹ 4913
Therefore, the required amount is ₹ 4,913.
10. The population of a place increased to 54000 in 2003 at a rate of 5% per annum
(i) find the population in 2001
(ii) what would be its population in 2005?
Solution:
(i) It’s given that population in the year 2003 = 54,000
54,000 = (Population in 2001) (1 + 5/100)2
54,000 = (Population in 2001) (105/100)2
Population in 2001 = 54000 x (100/105)2
= 48979.59
Therefore, the population in the year 2001 was approximately 48,980
(ii) Population in 2005 = 54000(1 + 5/100)2
= 54000(105/100)2
= 54000(21/20)2
= 59535
Therefore, the population in the year 2005 would be 59,535.
11. In a laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.
Solution:
The initial count of bacteria is given as 5,06,000
Bacteria at the end of 2 hours = 506000(1 + 2.5/100)2
= 506000(1 + 1/40)2
= 506000(41/40)2
= 531616.25
Therefore, the count of bacteria at the end of 2 hours will be 5,31,616 (approx.).
12. A scooter was bought at ₹ 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.
Solution:
Principal = Cost price of the scooter = ₹ 42,000
Depreciation = 8% of ₹ 42,000 per year
= (P x R x T)/100
= (42000 x 8 x 1)/100
= ₹ 3360
Thus, the value after 1 year = ₹ 42000 − ₹ 3360 = ₹ 38,640.
| Also Access |
| NCERT Exemplar for Class 8 Maths Chapter 8 |
| CBSE Notes for Class 8 Maths Chapter 8 |
NCERT Solutions for Class 8 Maths Chapter 8 – Comparing Quantities Summary
Chapter 8 of NCERT Class 8 Maths deals with the concept of ratios and percentages, along with other main topics and concepts.
The major concepts covered in this chapter include the following:
8.1 Recalling Ratios and Percentages
8.2 Finding the Increase or Decrease Per cent
8.3 Finding Discounts
8.3.1 Estimation in Percentages
8.4 Prices Related to Buying and Selling (Profit and Loss)
8.4.1 Finding Cost Price/Selling Price, Profit % Loss %
8.5 Sales Tax/Value Added Tax
8.6 Compound Interest
8.7 Deducing a Formula for Compound Interest
8.8 Rate Compounded Annually or Half Yearly (Semi-annually)
8.9 Applications of Compound Interest Formula
Access exercise-wise NCERT Solutions for Class 8 Maths Chapter 8 from the below links:
Exercise 8.1 Solutions 6 Questions (1 Long Answer Question, 5 Short Answer Questions)
Exercise 8.2 Solutions 10 Questions (4 Long Answer Questions, 6 Short Answer Questions)
Exercise 8.3 Solutions 12 Questions (6 Long Answer Questions, 6 Short Answer Questions)
NCERT Solutions for Class 8 Maths Chapter 8 – Comparing Quantities
Chapter 8 of NCERT Solutions for Class 8 Maths is really important to learn as the basic knowledge of tax, interest, profit, loss and much more are conveyed in this chapter. The concepts discussed in this chapter are:
- Discount is a reduction given on marked price. Discount = Marked Price – Sale Price.
- Discount can be calculated when the discount percentage is given. Discount = Discount % of the Marked Price
- Additional expenses made after buying an article are included in the cost price and are known as overhead expenses. C.P. = Buying price + Overhead expenses
- Sales tax is charged on the sale of an item by the government and is added to the Bill Amount. Sales tax = Tax% of Bill Amount.
- GST stands for Goods and Services Tax and is levied on the supply of goods or services or both.
- Compound interest is the interest calculated on the previous year’s amount (A = P + I)
Key Features of NCERT Solutions for Class 8 Maths Chapter 8 – Comparing Quantities
Learning the chapter Comparing Quantities familiarises students with:
- Slightly advanced problems involving applications on percentages, profit & loss, overhead expenses, discount, and tax.
- Difference between simple and compound interest (compounded yearly up to 3 years or half-yearly up to 3 steps only), arriving at the formula for compound interest through patterns and using it for simple problems.
- Direct variation – Simple and direct word problems
- Inverse variation – Simple and direct word problems
- Time & work problems– Simple and direct word problems
Disclaimer:
Dropped Topics – 8.2 Finding the Increase or decrease per cent, 8.4 Prices related to buying and selling, 8.4.1 Finding cost price/selling price, profit%/loss% and 8.8 Rate compounded annually or half
yearly.
Frequently Asked Questions on NCERT Solutions for Class 8 Maths Chapter 8
List out the concepts present in Frequently Asked Questions on NCERT Solutions for Class 8 Maths Chapter 8.
The major concepts are listed below:
8.1 Recalling Ratios and Percentages
8.2 Finding the Increase or Decrease Per cent
8.3 Finding Discounts
8.3.1 Estimation in percentages
8.4 Prices Related to Buying and Selling (Profit and Loss)
8.4.1 Finding Cost Price/Selling Price, Profit % Loss %
8.5 Sales Tax/Value Added Tax
8.6 Compound Interest
8.7 Deducing a Formula for Compound Interest
8.8 Rate Compounded Annually or Half Yearly (Semi-annually)
8.9 Applications of Compound Interest Formula



















Nice