NCERT Solutions Class 8 Maths Chapter 12 – Free PDF Download
NCERT Solutions for Class 8 Chapter 12 Exponents and Powers will help students aim for high marks in their examinations. Refer to the NCERT Class 8 Mathematics Exercise Solutions and practise the questions and answers based on the CBSE curriculum to understand the concepts covered in the chapter. We can say that an expression that represents repeated multiplication of the same factor is called a power. For example, in case of 42, the number 4 is called the base, and the number 2 is the exponent. An exponent corresponds to the number of times the base is utilised as a factor in an expression.
Download Exclusively Curated Chapter Notes for Class 8 Maths Chapter – 12 Exponents and Powers
Download Most Important Questions for Class 8 Maths Chapter – 12 Exponents and Powers
NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers
Access Answers of Maths NCERT Chapter 12 Exponents and Powers
Exercise 12.1 Page No: 197
1. Evaluate:
(i) 3-2 (ii) (-4)-2 (iii) (1/2)-5
Solution:
(i) 3-2 = (1/3)2
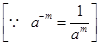
= 1/9
(ii) (-4)-2 = (1/-4)2
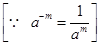
= 1/16
(iii) (1/2)-5 = (2/1)5
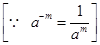
= 25
= 32
2. Simplify and express the result in power notation with a positive exponent:
(i) (-4)4 ÷(-4)8
(ii) (1/23)2
(iii) -(3)4×(5/3)4
(iv) (3-7÷3-10)×3-5
(v) 2-3×(-7)-3
Solution:
(i)
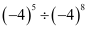
= (-4)5/(-4)8
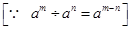
= (-4)5-8
= 1/(-4)3
(ii) (1/23)2
= 12/(23)2
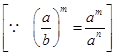
= 1/23×2 = 1/26
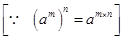
(iii) -(3)4×(5/3)4
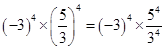
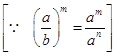
= (-1)4×34×(54/34 )
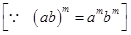
= 3(4-4)×54
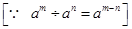
= 30×54 = 54
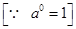
(iv) 
= (3-7/3-10)× 3-5
= 3-7 – (-10) × 3-5
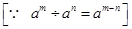
= 3(-7+10)×3-5
= 33×3-5
= 3(3+-5)
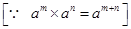
= 3-2
=1/32
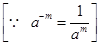
(v) 2-3×(-7) – 3
= (2×-7)-3
(Because am×bm = (ab)m)
= 1/(2×-7)3
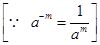
= 1/(-14)3
3. Find the value of:
(i) (30+4-1)×22
(ii) (2-1×4-1)÷2 – 2
(iii) (1/2)-2+(1/3)-2+(1/4)-2
(iv) (3-1+4-1+5-1)0
(v) {(-2/3)-2}2
Solution:
(i)(30+4– 1)×22 = (1+(1/4))×22

= ((4+1)/4 )×22
= (5/4)×22
= (5/22)×22
= 5×2(2-2)

= 5×20
= 5×1 = 5

(ii)(2-1×4-1)÷2-2
= [(1/2)×(1/4)] ÷(1/4)

= (1/2×1/22 )÷ 1/4
= 1/23÷1/4
= (1/8)×(4)
= 1/2
(iii) (1/2)-2+(1/3)-2+(1/4)-2
= (2-1)-2+(3-1)-2+(4-1)-2

= 2(-1×-2)+3(-1×-2)+4(-1×-2)

= 22+32+42
= 4+9+16
=29
(iv) (3-1+4-1+5-1)0
= 1

(v) {(-2/3)-2}2 = (-2/3)-2×2

= (-2/3)-4
= (-3/2)4

= 81/16
4. Evaluate:
(i) (8-1×53)/2-4
(ii) (5-1×2-2)×6-1
Solution:
(i) (8-1×53)/2-4


=


= 2×125 = 250
(ii) (5-1×2-2)×6-1


= (1/10)×1/6
= 1/60
5. Find the value of m for which 5m ÷ 5-3 = 55
Solution:
5m ÷ 5-3 = 55
5(m-(-3) ) = 55

5m+3 =55
Comparing exponents on both sides, we get
m+3 = 5
m = 5-3
m = 2
6. Evaluate:
(i)

(ii)

Solution:
(i)


= 3-4
= -1
(ii)


=


=

 =
=


= 512/125
7. Simplify the following:
(i)

(ii)

Solution:
(i)




=
 =
=

(ii)




=


=


=
 =
=

= 1×1×3125

= 3125
Exercise 12.2 Page No: 200
1. Express the following numbers in standard form.
(i) 0.0000000000085
(ii) 0.00000000000942
(iii) 6020000000000000
(iv) 0.00000000837
(v) 31860000000
Solution:
(i) 0.0000000000085 = 0.0000000000085×(1012/1012) = 8.5 ×10-12
(ii) 0.00000000000942 = 0.00000000000942×(1012/1012) = 9.42×10-12
(iii) 6020000000000000 = 6020000000000000×(1015/1015) = 6.02×1015
(iv) 0.00000000837 = 0.00000000837×(109/109) = 8.37×10-9
(v) 31860000000 = 31860000000×(1010/1010) = 3.186×1010
2. Express the following numbers in the usual form.
(i) 3.02×10-6
(ii) 4.5×104
(iii) 3×10-8
(iv) 1.0001×109
(v) 5.8×1012
(vi) 3.61492×106
Solution:
(i) 3.02×10-6 = 3.02/106 = 0 .00000302
(ii) 4.5×104 = 4.5×10000 = 45000
(iii) 3×10-8 = 3/108 = 0.00000003
(iv) 1.0001×109 = 1000100000
(v) 5.8×1012 = 5.8×1000000000000 = 5800000000000
(vi) 3.61492×106 = 3.61492×1000000 = 3614920
3. Express the number appearing in the following statements in standard form.
(i) 1 micron is equal to 1/1000000 m.
(ii) Charge of an electron is 0.000, 000, 000, 000, 000, 000, 16 coulomb.
(iii) Size of bacteria is 0.0000005 m
(iv) Size of a plant cell is 0.00001275 m
(v) Thickness of a thick paper is 0.07 mm
Solution:
(i) 1 micron = 1/1000000
= 1/106
= 1×10-6
(ii) Charge of an electron is 0.00000000000000000016 coulombs
= 0.00000000000000000016×1019/1019
= 1.6×10-19 coulomb
(iii) Size of bacteria = 0.0000005
= 5/10000000 = 5/107 = 5×10-7 m
(iv) Size of a plant cell is 0.00001275 m
= 0.00001275×105/105
= 1.275×10-5m
(v) Thickness of a thick paper = 0.07 mm
0.07 mm = 7/100 mm = 7/102 = 7×10-2 mm
4. In a stack, there are 5 books, each having a thickness of 20 mm and 5 paper sheets, each having a thickness of 0.016 mm. What is the total thickness of the stack?
Solution:
Thickness of one book = 20 mm
Thickness of 5 books = 20×5 = 100 mm
Thickness of one paper = 0.016 mm
Thickness of 5 papers = 0.016×5 = 0.08 mm
Total thickness of a stack = 100+0.08 = 100.08 mm
= 100.08×102/102 mm
 mm
mm
| Also Access |
| NCERT Exemplar for Class 8 Maths Chapter 12 |
| CBSE Notes for Class 8 Maths Chapter 12 |
NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers
These NCERT Solutions help students to gain a better understanding of the topic and learn the concepts easily. This learning material is designed by subject experts as per the latest CBSE syllabus prescribed by the Board. In Class 8 CBSE Chapter 12 of Maths, students will learn about how to write large numbers more conveniently using exponents and powers, express numbers in standard form, deal with negative exponents, various laws of exponents and many more.
NCERT Solutions for Class 8 Maths Chapter 12 Exercises:
Get detailed solutions for all the questions listed under below exercises:
Exercise 12.1 Solutions: 7 Questions (Short answers)
Exercise 12.2 Solutions: 4 Questions (Short answers)
NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers
NCERT Solutions for Class 8 Maths Chapter 12, Exponents and Powers, is about the law of exponents, powers and their applications.
The main topics covered in this chapter include the following:
| Exercise | Topic |
| 12.1 | Introduction |
| 12.2 | Powers with Negative Exponents |
| 12.3 | Laws of Exponents |
| 12.4 | Use of Exponents to Express Small Numbers in Standard Form |
Key Features of NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers
- The easy and simple language used will help students comprehend effortlessly.
- NCERT Solutions will help in boosting the confidence level of students.
- Subject experts have consolidated all exercise questions in one place, which could feature in the exam.
- All solutions are structured in an easy and logical language for quick revisions.
- NCERT Solutions are helpful for the preparation of competitive exams.













Very nice