NCERT Solutions for Class 8 Maths Chapter 11, Mensuration, consist of a set of questions and answers for all the textbook problems. All the solutions are prepared by BYJU’S experts, based on the latest CBSE syllabus and guidelines. The main aim is to give students the advantage of quality NCERT Solutions and a kick-start to their education. Our goal is to bring out the very best in students through additional skill-building exercises that are tailored to their grade levels, abilities and interests. Download free NCERT Solutions for Maths Chapter 11 and start practising offline.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Exercise 11.1
Access Other Exercise Solutions of Class 8 Maths Chapter 11 Mensuration
Exercise 11.2 Solutions : 11 Questions (Long answers)
Exercise 11.3 Solutions : 10 Questions (2 Short answers, 8 Long answers)
Exercise 11.4 Solutions : 8 Questions (2 Short answers, 6 Long answers)
Access Answers to NCERT Class 8 Maths Chapter 11 Mensuration Exercise 11.1 Page number 171
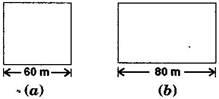
1. A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
Solution:
Side of a square = 60 m (Given)
And the length of rectangular field, l = 80 m (Given)
According to the question,
Perimeter of rectangular field = Perimeter of square field
2(l+b) = 4×Side (using formulas)
2(80+b) = 4×60
160+2b = 240
b = 40
Breadth of the rectangle is 40 m.
Now, Area of Square field
= (side)2
= (60)2 = 3600 m2
And Area of Rectangular field
= length×breadth = 80×40
= 3200 m2
Hence, area of the square field is larger.
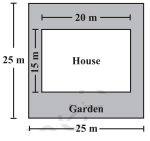
2. Mrs.Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of Rs. 55 per m2.
Solution:
Side of a square plot = 25 m
Formula: Area of square plot = square of a side = (side)2
= (25)2 = 625
Therefore the area of a square plot is 625 m2
Length of the house = 20 m and
Breadth of the house = 15 m
Area of the house = length×breadth
= 20×15 = 300 m2
Area of garden = Area of square plot – Area of house
= 625–300 = 325 m2
∵ Cost of developing the garden per sq. m is Rs. 55
Cost of developing the garden 325 sq. m = Rs. 55×325
= Rs. 17,875
Hence, total cost of developing a garden around is Rs. 17,875.
3. The shape of a garden is rectangular in the middle and semi-circular at the ends as shown in the diagram. Find the area and the perimeter of this garden [Length of rectangle is 20 – (3.5 + 3.5 meters)]

Solution::
Given: Total length = 20 m
Diameter of semi circle = 7 m
Radius of semi circle = 7/2 = 3.5 m
Length of the rectangular field
= 20-(3.5+3.5) = 20-7 = 13 m
Breadth of the rectangular field = 7 m
Area of the rectangular field = l×b
= 13×7= 91m2
Area of two semi circles = 2×(1/2)×π×r2
= 2×(1/2)×22/7×3.5×3.5
= 38.5 m2
Area of garden = 91+38.5 = 129.5 m2
Now Perimeter of two semi circles = 2πr = 2×(22/7)×3.5 = 22 m
And Perimeter of the garden = 22+13+13
= 48 m. Answer
4. A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? [If required you can split the tiles in whatever way you want to fill up the corners]
Solution:
Given: Base of flooring tile = 24 cm = 0.24 m
Corresponding height of a flooring tile= 10 cm = 0.10 m
Now Area of flooring tile= Base×Altitude
= 0.24×0.10
= 0.024
Area of flooring tile is 0.024m2
Number of tiles required to cover the floor= Area of floor/Area of one tile = 1080/0.024
= 45000 tiles
Hence, 45000 tiles are required to cover the floor.
5. An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression C = 2πr ,where r is the radius of the circle.

Solution:
(a) Radius = Diameter/2 = 2.8/2 cm = 1.4 cm
Circumference of semi-circle = πr
= (22/7)×1.4 = 4.4
Circumference of semi-circle is 4.4 cm
Total distance covered by the ant= Circumference of semi -circle+Diameter
= 4.4+2.8 = 7.2 cm
(b) Diameter of semi-circle = 2.8 cm
Radius = Diameter/2 = 2.8/2 = 1.4 cm
Circumference of semi-circle = r
= (22/7)×1.4 = 4.4 cm
Total distance covered by the ant= 1.5+2.8+1.5+4.4 = 10.2 cm
(c) Diameter of semi-circle = 2.8 cm
Radius = Diameter/2 = 2.8/2
= 1.4 cm
Circumference of semi-circle = π r
= (22/7)×1.4
= 4.4 cm
Total distance covered by the ant = 2+2+4.4 = 8.4 cm
After analysing the results of three figures, we concluded that for figure (b) food piece, the ant would take a longer round.
This exercise is based on the areas of geometrical shapes and their combinations if certain measurements are given. At the end of the section, students can understand the concepts easily and solve real-life problems at their own pace such as; What is the total length of the fence surrounding a rectangular park whose dimensions are given, how many flooring tiles are required to cover a floor of an area if base and height of a parallelogram tile are given and many more. Download NCERT Class 8 Maths Solutions and practise such problems.
Also, explore –






Nice
Very good
Nice 🙂