NCERT Solutions for Class 9 Maths Chapter 2 - Polynomials Exercise 2.5

NCERT Solutions Class 9 Maths Chapter 2 – Polynomials Exercise 2.5 are given here. These NCERT Maths solutions are created by our subject experts, who make it easy for students to learn. The students use NCERT Class 9 Maths Solutions for reference while solving the exercise problems. The fifth exercise in Polynomials- Exercise 2.5 discusses the Algebraic Identities.

The experts provide a detailed and stepwise explanation of each answer to the questions given in the exercises in the NCERT textbook for Class 9. The NCERT solutions are always prepared by following NCERT guidelines so that it should cover the whole syllabus accordingly. These are very helpful in scoring well in board examinations.

NCERT Solutions for Class 9 Maths Chapter 2- Polynomials Exercise 2.5

Download PDF

carouselExampleControls111

Previous



Next

Access Other Exercise Solutions of Class 9 Maths Chapter 2- Polynomials

The Exercise wise links for NCERT Class 9 Solutions Maths Chapter 2 are given below.

Exercise 2.1 Solutions 5 Questions
Exercise 2.2 Solutions 4 Questions
Exercise 2.3 Solutions 3 Questions
Exercise 2.4 Solutions 5 Questions

Access Answers to NCERT Class 9 Maths Chapter 2 – Polynomials Exercise 2.5

1. Use suitable identities to find the following products:

(i) (x+4)(x +10) 

Solution:

Using the identity, (x+a)(x+b) = x ²+(a+b)x+ab

We get,

(x+4)(x+10) = x²+(4+10)x+(4×10)

= x²+14x+40

(ii) (x+8)(x –10)     

Solution:

Using the identity, (x+a)(x+b) = x ²+(a+b)x+ab

We get,

(x+8)(x−10) = x²+(8+(−10))x+(8×(−10))

= x²+(8−10)x–80

= x²−2x−80

(iii) (3x+4)(3x–5)

Solution:

Using the identity, (x+a)(x+b) = x ²+(a+b)x+ab

We get,

(3x+4)(3x−5) = (3x)²+[4+(−5)]3x+4×(−5)

= 9x²+3x(4–5)–20

= 9x²–3x–20

(iv) (y²+3/2)(y²-3/2)

Solution:

Using the identity, (x+y)(x–y) = x²–y ²

We get,

(y²+3/2)(y²–3/2) = (y²)²–(3/2)²

= y⁴–9/4

2. Evaluate the following products without multiplying directly:

(i) 103×107

Solution:

103×107= (100+3)×(100+7)

Using identity, [(x+a)(x+b) = x²+(a+b)x+ab

Here, x = 100

a = 3

b = 7

We get, 103×107 = (100+3)×(100+7)

= (100)²+(3+7)100+(3×7)

= 10000+1000+21

= 11021

(ii) 95×96  

Solution:

95×96 = (100-5)×(100-4)

Using identity, [(x-a)(x-b) = x²-(a+b)x+ab

Here, x = 100

a = -5

b = -4

We get, 95×96 = (100-5)×(100-4)

= (100)²+100(-5+(-4))+(-5×-4)

= 10000-900+20

= 9120

(iii) 104×96

Solution:

104×96 = (100+4)×(100–4)

Using identity, [(a+b)(a-b)= a²-b²]

Here, a = 100

b = 4

We get, 104×96 = (100+4)×(100–4)

= (100)²–(4)²

= 10000–16

= 9984

3. Factorize the following using appropriate identities:

(i) 9x²+6xy+y²

Solution:

9x²+6xy+y² = (3x)²+(2×3x×y)+y²

Using identity, x²+2xy+y² = (x+y)²

Here, x = 3x

y = y

9x²+6xy+y² = (3x)²+(2×3x×y)+y²

= (3x+y)²

= (3x+y)(3x+y)

(ii) 4y²−4y+1

Solution:

4y²−4y+1 = (2y)²–(2×2y×1)+1

Using identity, x² – 2xy + y² = (x – y)²

Here, x = 2y

y = 1

4y²−4y+1 = (2y)²–(2×2y×1)+1²

= (2y–1)²

= (2y–1)(2y–1)

(iii)  x²–y²/100

Solution:

x²–y²/100 = x²–(y/10)²

Using identity, x²-y² = (x-y)(x+y)

Here, x = x

y = y/10

x²–y²/100 = x²–(y/10)²

= (x–y/10)(x+y/10)

4. Expand each of the following, using suitable identities:

(i) (x+2y+4z)²

(ii) (2x−y+z)²

(iii) (−2x+3y+2z)²

(iv) (3a –7b–c)²

(v) (–2x+5y–3z)²

(vi) ((1/4)a-(1/2)b +1)²

Solution:

(i) (x+2y+4z)²

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = x

y = 2y

z = 4z

(x+2y+4z)² = x²+(2y)²+(4z)²+(2×x×2y)+(2×2y×4z)+(2×4z×x)

= x²+4y²+16z²+4xy+16yz+8xz

(ii) (2x−y+z)² 

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = 2x

y = −y

z = z

(2x−y+z)² = (2x)²+(−y)²+z²+(2×2x×−y)+(2×−y×z)+(2×z×2x)

= 4x²+y²+z²–4xy–2yz+4xz

(iii) (−2x+3y+2z)²

Solution:

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = −2x

y = 3y

z = 2z

(−2x+3y+2z)² = (−2x)²+(3y)²+(2z)²+(2×−2x×3y)+(2×3y×2z)+(2×2z×−2x)

= 4x²+9y²+4z²–12xy+12yz–8xz

(iv) (3a –7b–c)²

Solution:

Using identity (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = 3a

y = – 7b

z = – c

(3a –7b– c)² = (3a)²+(– 7b)²+(– c)²+(2×3a ×– 7b)+(2×– 7b ×– c)+(2×– c ×3a)

= 9a² + 49b² + c²– 42ab+14bc–6ca

(v) (–2x+5y–3z)²

Solution:

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = –2x

y = 5y

z = – 3z

(–2x+5y–3z)² = (–2x)²+(5y)²+(–3z)²+(2×–2x × 5y)+(2× 5y×– 3z)+(2×–3z ×–2x)

= 4x²+25y² +9z²– 20xy–30yz+12zx

(vi) ((1/4)a-(1/2)b+1)²

Solution:

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

Here, x = (1/4)a

y = (-1/2)b

z = 1

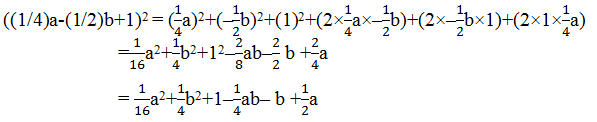
5. Factorize:

(i) 4x²+9y²+16z²+12xy–24yz–16xz

(ii ) 2x²+y²+8z²–2√2xy+4√2yz–8xz

Solution:

(i) 4x²+9y²+16z²+12xy–24yz–16xz

Using identity, (x+y+z)² = x²+y²+z²+2xy+2yz+2zx

We can say that, x²+y²+z²+2xy+2yz+2zx = (x+y+z)²

4x²+9y²+16z²+12xy–24yz–16xz = (2x)²+(3y)²+(−4z)²+(2×2x×3y)+(2×3y×−4z)+(2×−4z×2x)

= (2x+3y–4z)²

= (2x+3y–4z)(2x+3y–4z)

(ii) 2x²+y²+8z²–2√2xy+4√2yz–8xz

Using identity, (x +y+z)² = x²+y²+z²+2xy+2yz+2zx

We can say that, x²+y²+z²+2xy+2yz+2zx = (x+y+z)²

2x²+y²+8z²–2√2xy+4√2yz–8xz

= (-√2x)²+(y)²+(2√2z)²+(2×-√2x×y)+(2×y×2√2z)+(2×2√2×−√2x)

= (−√2x+y+2√2z)²

= (−√2x+y+2√2z)(−√2x+y+2√2z)

6. Write the following cubes in expanded form:

(i) (2x+1)³

(ii) (2a−3b)³

(iii) ((3/2)x+1)³

(iv) (x−(2/3)y)³

Solution:

(i) (2x+1)³

Using identity,(x+y)³ = x³+y³+3xy(x+y)

(2x+1)³= (2x)³+1³+(3×2x×1)(2x+1)

= 8x³+1+6x(2x+1)

= 8x³+12x²+6x+1

(ii) (2a−3b)³

Using identity,(x–y)³ = x³–y³–3xy(x–y)

(2a−3b)³ = (2a)³−(3b)³–(3×2a×3b)(2a–3b)

= 8a³–27b³–18ab(2a–3b)

= 8a³–27b³–36a²b+54ab²

(iii) ((3/2)x+1)³

Using identity,(x+y)³ = x³+y³+3xy(x+y)

((3/2)x+1)³=((3/2)x)³+1³+(3×(3/2)x×1)((3/2)x +1)

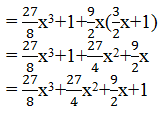
(iv)  (x−(2/3)y)³

Using identity, (x –y)³ = x³–y³–3xy(x–y)

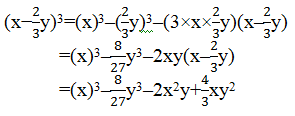
7. Evaluate the following using suitable identities: 

(i) (99)³

(ii) (102)³

(iii) (998)³

Solutions:

(i) (99)³

Solution:

We can write 99 as 100–1

Using identity, (x –y)³ = x³–y³–3xy(x–y)

(99)³ = (100–1)³

= (100)³–1³–(3×100×1)(100–1)

= 1000000 –1–300(100 – 1)

= 1000000–1–30000+300

= 970299

(ii) (102)³

Solution:

We can write 102 as 100+2

Using identity,(x+y)³ = x³+y³+3xy(x+y)

(100+2)³ =(100)³+2³+(3×100×2)(100+2)

= 1000000 + 8 + 600(100 + 2)

= 1000000 + 8 + 60000 + 1200

= 1061208

(iii) (998)³

Solution:

We can write 99 as 1000–2

Using identity,(x–y)³ = x³–y³–3xy(x–y)

(998)³ =(1000–2)³

=(1000)³–2³–(3×1000×2)(1000–2)

= 1000000000–8–6000(1000– 2)

= 1000000000–8- 6000000+12000

= 994011992

8. Factorise each of the following:

(i) 8a³+b³+12a²b+6ab²

(ii) 8a³–b³–12a²b+6ab²

(iii) 27–125a³–135a +225a²   

(iv) 64a³–27b³–144a²b+108ab²

(v) 27p³–(1/216)−(9/2) p²+(1/4)p

Solutions:

(i) 8a³+b³+12a²b+6ab²

Solution:

The expression, 8a³+b³+12a²b+6ab² can be written as (2a)³+b³+3(2a)²b+3(2a)(b)²

8a³+b³+12a²b+6ab² = (2a)³+b³+3(2a)²b+3(2a)(b)²

= (2a+b)³

= (2a+b)(2a+b)(2a+b)

Here, the identity, (x +y)³ = x³+y³+3xy(x+y) is used.

(ii) 8a³–b³–12a²b+6ab²

Solution:

The expression, 8a³–b³−12a²b+6ab² can be written as (2a)³–b³–3(2a)²b+3(2a)(b)²

8a³–b³−12a²b+6ab² = (2a)³–b³–3(2a)²b+3(2a)(b)²

= (2a–b)³

= (2a–b)(2a–b)(2a–b)

Here, the identity,(x–y)³ = x³–y³–3xy(x–y) is used.

(iii) 27–125a³–135a+225a² 

Solution:

The expression, 27–125a³–135a +225a² can be written as 3³–(5a)³–3(3)²(5a)+3(3)(5a)²

27–125a³–135a+225a² =
3³–(5a)³–3(3)²(5a)+3(3)(5a)²

= (3–5a)³

= (3–5a)(3–5a)(3–5a)

Here, the identity, (x–y)³ = x³–y³-3xy(x–y) is used.

(iv) 64a³–27b³–144a²b+108ab²

Solution:

The expression, 64a³–27b³–144a²b+108ab²can be written as (4a)³–(3b)³–3(4a)²(3b)+3(4a)(3b)²

64a³–27b³–144a²b+108ab²=
(4a)³–(3b)³–3(4a)²(3b)+3(4a)(3b)²

=(4a–3b)³

=(4a–3b)(4a–3b)(4a–3b)

Here, the identity, (x – y)³ = x³ – y³ – 3xy(x – y) is used.

(v) 27p³– (1/216)−(9/2) p²+(1/4)p

Solution:

The expression, 27p³–(1/216)−(9/2) p²+(1/4)p can be written as

(3p)³–(1/6)³−(9/2) p²+(1/4)p = (3p)³–(1/6)³−3(3p)(1/6)(3p – 1/6)

Using (x – y)³ = x³ – y³ – 3xy (x – y)

27p³–(1/216)−(9/2) p²+(1/4)p = (3p)³–(1/6)³−3(3p)(1/6)(3p – 1/6)

Taking x = 3p and y = 1/6

= (3p–1/6)³

= (3p–1/6)(3p–1/6)(3p–1/6)

9. Verify:

(i) x³+y³ = (x+y)(x²–xy+y²)

(ii) x³–y³ = (x–y)(x²+xy+y²)

Solutions:

(i) x³+y³ = (x+y)(x²–xy+y²)

We know that, (x+y)³ = x³+y³+3xy(x+y)

⇒ x³+y³ = (x+y)³–3xy(x+y)

⇒ x³+y³ = (x+y)[(x+y)²–3xy]

Taking (x+y) common ⇒ x³+y³ = (x+y)[(x²+y²+2xy)–3xy]

⇒ x³+y³ = (x+y)(x²+y²–xy)

(ii) x³–y³ = (x–y)(x²+xy+y²) 

We know that,(x–y)³ = x³–y³–3xy(x–y)

⇒ x³−y³ = (x–y)³+3xy(x–y)

⇒ x³−y³ = (x–y)[(x–y)²+3xy]

Taking (x+y) common ⇒ x³−y³ = (x–y)[(x²+y²–2xy)+3xy]

⇒ x³+y³ = (x–y)(x²+y²+xy)

10. Factorize each of the following:

(i) 27y³+125z³

(ii) 64m³–343n³

Solutions:

(i) 27y³+125z³

The expression, 27y³+125z³ can be written as (3y)³+(5z)³

27y³+125z³ = (3y)³+(5z)³

We know that, x³+y³ = (x+y)(x²–xy+y²)

27y³+125z³ = (3y)³+(5z)³

= (3y+5z)[(3y)²–(3y)(5z)+(5z)²]

= (3y+5z)(9y²–15yz+25z²)

(ii) 64m³–343n³

The expression, 64m³–343n³can be written as (4m)³–(7n)³

64m³–343n³ =
(4m)³–(7n)³

We know that, x³–y³ = (x–y)(x²+xy+y²)

64m³–343n³ = (4m)³–(7n)³

= (4m–7n)[(4m)²+(4m)(7n)+(7n)²]

= (4m–7n)(16m²+28mn+49n²)

11. Factorise: 27x³+y³+z³–9xyz 

Solution:

The expression 27x³+y³+z³–9xyz can be written as (3x)³+y³+z³–3(3x)(y)(z)

27x³+y³+z³–9xyz  = (3x)³+y³+z³–3(3x)(y)(z)

We know that, x³+y³+z³–3xyz = (x+y+z)(x²+y²+z²–xy –yz–zx)

27x³+y³+z³–9xyz  = (3x)³+y³+z³–3(3x)(y)(z)

= (3x+y+z)[(3x)²+y²+z²–3xy–yz–3xz]

= (3x+y+z)(9x²+y²+z²–3xy–yz–3xz)

12. Verify that:

x³+y³+z³–3xyz = (1/2) (x+y+z)[(x–y)²+(y–z)²+(z–x)²]

Solution:

We know that,

x³+y³+z³−3xyz = (x+y+z)(x²+y²+z²–xy–yz–xz)

⇒ x³+y³+z³–3xyz = (1/2)(x+y+z)[2(x²+y²+z²–xy–yz–xz)]

= (1/2)(x+y+z)(2x²+2y²+2z²–2xy–2yz–2xz)

= (1/2)(x+y+z)[(x²+y²−2xy)+(y²+z²–2yz)+(x²+z²–2xz)]

= (1/2)(x+y+z)[(x–y)²+(y–z)²+(z–x)²]

13. If  x+y+z = 0, show that x³+y³+z³ = 3xyz.

Solution:

We know that,

x³+y³+z³-3xyz = (x +y+z)(x²+y²+z²–xy–yz–xz)

Now, according to the question, let (x+y+z) = 0,

then, x³+y³+z³ -3xyz = (0)(x²+y²+z²–xy–yz–xz)

⇒ x³+y³+z³–3xyz = 0

⇒ x³+y³+z³ = 3xyz

Hence Proved

14. Without actually calculating the cubes, find the value of each of the following:

(i) (−12)³+(7)³+(5)³

(ii) (28)³+(−15)³+(−13)³

Solution:

(i) (−12)³+(7)³+(5)³

Let a = −12

b = 7

c = 5

We know that if x+y+z = 0, then x³+y³+z³=3xyz.

Here, −12+7+5=0

(−12)³+(7)³+(5)³ = 3xyz

= 3×-12×7×5

= -1260

(ii) (28)³+(−15)³+(−13)³

Solution:

(28)³+(−15)³+(−13)³

Let a = 28

b = −15

c = −13

We know that if x+y+z = 0, then x³+y³+z³ = 3xyz.

Here, x+y+z = 28–15–13 = 0

(28)³+(−15)³+(−13)³ = 3xyz

= 0+3(28)(−15)(−13)

= 16380

15. Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given: 

(i) Area : 25a²–35a+12

(ii) Area : 35y²+13y–12

Solution:

(i) Area : 25a²–35a+12

Using the splitting the middle term method,

We have to find a number whose sum = -35 and product =25×12=300

We get -15 and -20 as the numbers [-15+-20=-35 and -15×-20=300]

25a²–35a+12 = 25a²–15a−20a+12

= 5a(5a–3)–4(5a–3)

= (5a–4)(5a–3)

Possible expression for length  = 5a–4

Possible expression for breadth  = 5a –3

(ii) Area : 35y²+13y–12

Using the splitting the middle term method,

We have to find a number whose sum = 13 and product = 35×-12 = 420

We get -15 and 28 as the numbers [-15+28 = 13 and -15×28=420]

35y²+13y–12 = 35y²–15y+28y–12

= 5y(7y–3)+4(7y–3)

= (5y+4)(7y–3)

Possible expression for length  = (5y+4)

Possible expression for breadth  = (7y–3)

16. What are the possible expressions for the dimensions of the cuboids whose volumes are given below? 

(i) Volume : 3x²–12x

(ii) Volume : 12ky²+8ky–20k

Solution:

(i) Volume : 3x²–12x

3x²–12x can be written as 3x(x–4) by taking 3x out of both the terms.

Possible expression for length = 3

Possible expression for breadth = x

Possible expression for height = (x–4)

(ii) Volume:
12ky²+8ky–20k

12ky²+8ky–20k can be written as 4k(3y²+2y–5) by taking 4k out of both the terms.

12ky²+8ky–20k = 4k(3y²+2y–5)

= 4k(3y²+5y–3y–5)

= 4k[y(3y+5)–1(3y+5)]

= 4k(3y+5)(y–1)

Possible expression for length = 4k

Possible expression for breadth = (3y +5)

Possible expression for height = (y -1)