NCERT Solutions Class 9 Maths Chapter 2 Polynomials Exercise 2.4 are provided here. These NCERT Maths solutions are prepared by our subject experts, which makes it easy for students to learn. The students use NCERT Class 9 Maths Solutions for reference while solving the exercise problems. The fourth exercise in Polynomials- Exercise 2.4 discusses the Factorisation of Polynomials.
The solutions provide a detailed and stepwise explanation of each answer to the questions given in the exercises in the NCERT textbook for Class 9. The NCERT solutions are always prepared by following NCERT guidelines so that it covers the whole syllabus accordingly. These are very helpful in scoring well in board examinations.
NCERT Solutions for Class 9 Maths Chapter 2- Polynomials Exercise 2.4
Access other exercise solutions of Class 9 Maths Chapter 2 – Polynomials
The links below provide students with detailed NCERT Solutions for Class 9 Maths Chapter 2.
Exercise 2.1 Solutions 5 Questions
Exercise 2.2 Solutions 4 Questions
Exercise 2.3 Solutions 3 Questions
Exercise 2.5 Solutions 16 Questions
Access Answers to Maths NCERT Class 9 Chapter 2 – Polynomials Exercise 2.4
1. Determine which of the following polynomials has (x + 1) a factor:
(i) x3+x2+x+1
Solution:
Let p(x) = x3+x2+x+1
The zero of x+1 is -1. [x+1 = 0 means x = -1]
p(−1) = (−1)3+(−1)2+(−1)+1
= −1+1−1+1
= 0
∴By factor theorem, x+1 is a factor of x3+x2+x+1
(ii) x4+x3+x2+x+1
Solution:
Let p(x)= x4+x3+x2+x+1
The zero of x+1 is -1. . [x+1= 0 means x = -1]
p(−1) = (−1)4+(−1)3+(−1)2+(−1)+1
= 1−1+1−1+1
= 1 ≠ 0
∴By factor theorem, x+1 is not a factor of x4 + x3 + x2 + x + 1
(iii) x4+3x3+3x2+x+1
Solution:
Let p(x)= x4+3x3+3x2+x+1
The zero of x+1 is -1.
p(−1)=(−1)4+3(−1)3+3(−1)2+(−1)+1
=1−3+3−1+1
=1 ≠ 0
∴By factor theorem, x+1 is not a factor of x4+3x3+3x2+x+1
(iv) x3 – x2– (2+√2)x +√2
Solution:
Let p(x) = x3–x2–(2+√2)x +√2
The zero of x+1 is -1.
p(−1) = (-1)3–(-1)2–(2+√2)(-1) + √2 = −1−1+2+√2+√2
= 2√2 ≠ 0
∴By factor theorem, x+1 is not a factor of x3–x2–(2+√2)x +√2
2. Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
(i) p(x) = 2x3+x2–2x–1, g(x) = x+1
Solution:
p(x) = 2x3+x2–2x–1, g(x) = x+1
g(x) = 0
⇒ x+1 = 0
⇒ x = −1
∴Zero of g(x) is -1.
Now,
p(−1) = 2(−1)3+(−1)2–2(−1)–1
= −2+1+2−1
= 0
∴By factor theorem, g(x) is a factor of p(x).
(ii) p(x)=x3+3x2+3x+1, g(x) = x+2
Solution:
p(x) = x3+3x2+3x+1, g(x) = x+2
g(x) = 0
⇒ x+2 = 0
⇒ x = −2
∴ Zero of g(x) is -2.
Now,
p(−2) = (−2)3+3(−2)2+3(−2)+1
= −8+12−6+1
= −1 ≠ 0
∴By factor theorem, g(x) is not a factor of p(x).
(iii) p(x)=x3–4x2+x+6, g(x) = x–3
Solution:
p(x) = x3–4x2+x+6, g(x) = x -3
g(x) = 0
⇒ x−3 = 0
⇒ x = 3
∴ Zero of g(x) is 3.
Now,
p(3) = (3)3−4(3)2+(3)+6
= 27−36+3+6
= 0
∴By factor theorem, g(x) is a factor of p(x).
3. Find the value of k, if x–1 is a factor of p(x) in each of the following cases:
(i) p(x) = x2+x+k
Solution:
If x-1 is a factor of p(x), then p(1) = 0
By Factor Theorem
⇒ (1)2+(1)+k = 0
⇒ 1+1+k = 0
⇒ 2+k = 0
⇒ k = −2
(ii) p(x) = 2x2+kx+√2
Solution:
If x-1 is a factor of p(x), then p(1)=0
⇒ 2(1)2+k(1)+√2 = 0
⇒ 2+k+√2 = 0
⇒ k = −(2+√2)
(iii) p(x) = kx2–√2x+1
Solution:
If x-1 is a factor of p(x), then p(1)=0
By Factor Theorem
⇒ k(1)2-√2(1)+1=0
⇒ k = √2-1
(iv) p(x)=kx2–3x+k
Solution:
If x-1 is a factor of p(x), then p(1) = 0
By Factor Theorem
⇒ k(1)2–3(1)+k = 0
⇒ k−3+k = 0
⇒ 2k−3 = 0
⇒ k= 3/2
4. Factorize:
(i) 12x2–7x+1
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = -7 and product =1×12 = 12
We get -3 and -4 as the numbers [-3+-4=-7 and -3×-4 = 12]
12x2–7x+1= 12x2-4x-3x+1
= 4x(3x-1)-1(3x-1)
= (4x-1)(3x-1)
(ii) 2x2+7x+3
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = 7 and product = 2×3 = 6
We get 6 and 1 as the numbers [6+1 = 7 and 6×1 = 6]
2x2+7x+3 = 2x2+6x+1x+3
= 2x (x+3)+1(x+3)
= (2x+1)(x+3)
(iii) 6x2+5x-6
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = 5 and product = 6×-6 = -36
We get -4 and 9 as the numbers [-4+9 = 5 and -4×9 = -36]
6x2+5x-6 = 6x2+9x–4x–6
= 3x(2x+3)–2(2x+3)
= (2x+3)(3x–2)
(iv) 3x2–x–4
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = -1 and product = 3×-4 = -12
We get -4 and 3 as the numbers [-4+3 = -1 and -4×3 = -12]
3x2–x–4 = 3x2–4x+3x–4
= x(3x–4)+1(3x–4)
= (3x–4)(x+1)
5. Factorize:
(i) x3–2x2–x+2
Solution:
Let p(x) = x3–2x2–x+2
Factors of 2 are ±1 and ± 2
Now,
p(x) = x3–2x2–x+2
p(−1) = (−1)3–2(−1)2–(−1)+2
= −1−2+1+2
= 0
Therefore, (x+1) is the factor of p(x)
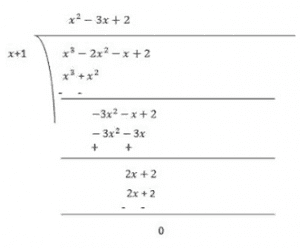
Now, Dividend = Divisor × Quotient + Remainder
(x+1)(x2–3x+2) = (x+1)(x2–x–2x+2)
= (x+1)(x(x−1)−2(x−1))
= (x+1)(x−1)(x-2)
(ii) x3–3x2–9x–5
Solution:
Let p(x) = x3–3x2–9x–5
Factors of 5 are ±1 and ±5
By trial method, we find that
p(5) = 0
So, (x-5) is factor of p(x)
Now,
p(x) = x3–3x2–9x–5
p(5) = (5)3–3(5)2–9(5)–5
= 125−75−45−5
= 0
Therefore, (x-5) is the factor of p(x)
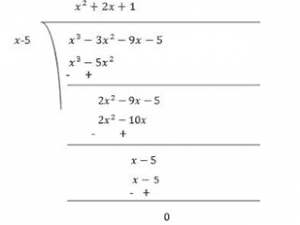
Now, Dividend = Divisor × Quotient + Remainder
(x−5)(x2+2x+1) = (x−5)(x2+x+x+1)
= (x−5)(x(x+1)+1(x+1))
= (x−5)(x+1)(x+1)
(iii) x3+13x2+32x+20
Solution:
Let p(x) = x3+13x2+32x+20
Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20
By trial method, we find that
p(-1) = 0
So, (x+1) is factor of p(x)
Now,
p(x)= x3+13x2+32x+20
p(-1) = (−1)3+13(−1)2+32(−1)+20
= −1+13−32+20
= 0
Therefore, (x+1) is the factor of p(x)
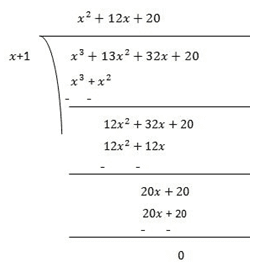
Now, Dividend = Divisor × Quotient +Remainder
(x+1)(x2+12x+20) = (x+1)(x2+2x+10x+20)
= (x+1)x(x+2)+10(x+2)
= (x+1)(x+2)(x+10)
(iv) 2y3+y2–2y–1
Solution:
Let p(y) = 2y3+y2–2y–1
Factors = 2×(−1)= -2 are ±1 and ±2
By trial method, we find that
p(1) = 0
So, (y-1) is factor of p(y)
Now,
p(y) = 2y3+y2–2y–1
p(1) = 2(1)3+(1)2–2(1)–1
= 2+1−2
= 0
Therefore, (y-1) is the factor of p(y)

Now, Dividend = Divisor × Quotient + Remainder
(y−1)(2y2+3y+1) = (y−1)(2y2+2y+y+1)
= (y−1)(2y(y+1)+1(y+1))
= (y−1)(2y+1)(y+1)








Thanks
Good
Nice
Thanks
I’m very happy that I founded this website means byjus it’s very good app
Thanks
Thanks it really very helpful👍🏻👍🏻
It is excellent and all answers are appropriate
Thanks it was very helpful 😊
I really loved this app 😭 💖
Thankyou