Conservation of Momentum

Conservation of Linear Momentum:

Conservation of linear momentum is based on Newton’s second law of motion, which states that in an isolated system, the total momentum remains the same. Let’s consider the following example,

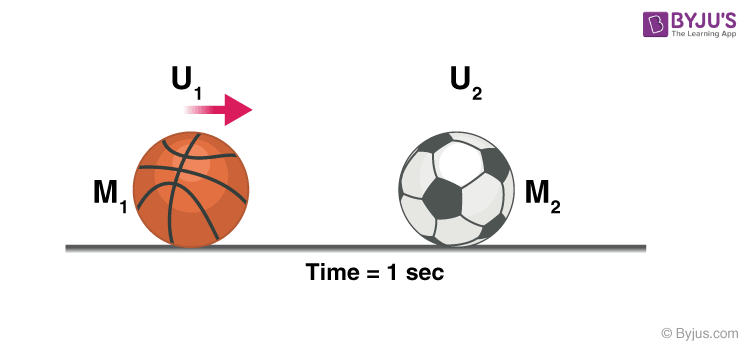
Remember: In the above experiment, we did not consider any loss of energy due to friction, heat, etc. and all the collisions were elastic in nature, i.e. there was a total transfer of energy, actual observations may differ.

Let’s consider a case where a football of mass M₂ is resting on the ground, and a bowling ball with a comparatively heavier mass of M₁ is thrown at the football at a velocity of U₁.

When the bowling ball hits the football the energy is transferred and the bowling ball loses some velocity and moves at a new velocity V₁, the football moves at velocity V₂, why did the football move?

To conserve linear momentum, i.e. the bowling ball had an initial momentum of M₁ so as M₂ < M₁ and the momentum of football should be equal to the momentum lost by the bowling ball according to the law of conservation of momentum, the football had no other option than moving at a velocity V₂.

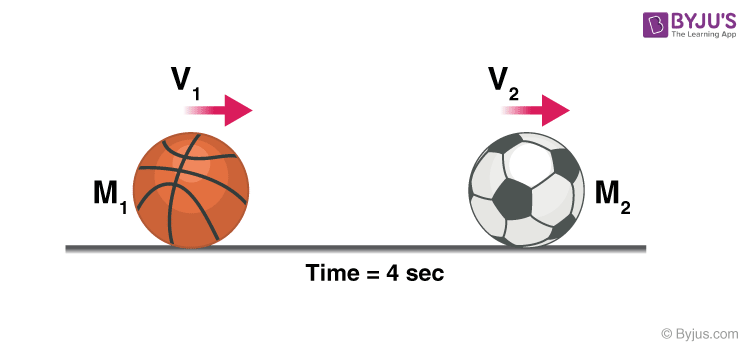
Read More: Conservation of Momentum

Formula:

Mathematically it is given by,

\(\begin{array}{l}m_1u_1~+~m_2u_2 = m_1v_1~+~m_2v_2\end{array} \)

\(\begin{array}{l}Note: \,\,m_1u_1 \neq m_1v_1\end{array} \)

Where,

m₁ is mass of the bowling ball

m₂ is the mass of the football

u₁ and u₂ are the initial velocities and v₁ and v₂ are the final velocities.

Even though the momentum of each particle changes, altogether the momentum of the system remains constant as long as there is no external force acting on it. In a head-to-head car accident, the momentum is transferred from one car to the other, but so much force is applied that the car structure cannot handle it, this is why a car wrecks. If the cars were able to deal with the amount of force, and the collision was elastic they both will move in opposite directions, considering their weights are the same.

In short, momentum is always conserved in any collision, whether it be an elastic or a non-elastic collision, though kinetic energy is not conserved in a non-elastic collision, the kinetic energy is converted into heat energy or potential energy, etc.

Example of Conservation of Momentum

Consider this example of a balloon, the particles of gas move rapidly colliding with each other and the walls of the balloon, even though the particles themselves move faster and slower when they lose or gain momentum when they collide, the total momentum of the system remains the same.

Hence, the balloon doesn’t change in size, if we add external energy by heating it, the balloon should expand because it increases the velocity of the particles and this increases their momentum, in turn, increasing the force exerted by them on the walls of the balloon.

Application of Law of Conservation of Momentum

Having said so the energy of a system is always conserved, one of the best applications of the law of conservation of momentum would be in space travel, there is no medium in space to exert a force on, then how do rockets travel?

Well, they eject matter at a very high speed, so in an isolated system, the momentum should remain constant therefore, the rocket will move in the opposite direction with the same momentum as that of the exhaust.

Watch the video and solve important questions in the chapter Force and Laws of Motion Class 9

Frequently Asked Questions – FAQs

Q1

What does the law of conservation of momentum state?

The law of conservation of momentum states that in an isolated system the total momentum of two or more bodies acting upon each other remains constant unless an external force is applied. Therefore, momentum can neither be created nor destroyed.

Q2

The law of conservation of momentum is based on which law of motion?

The law of conservation of momentum is based on Newton’s third law of motion which states that every force has a reciprocating equal and opposite force.

Q3

What is the real-life example of the law of conservation of momentum?

The thrust that you feel at the time of firing is one of the real-life examples of the conservation of momentum.

Q4

What is the law of conservation of momentum formula?

The momentum observation principle can be mathematically represented as:
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
In the equation, m¹ and m₂ are masses of the bodies, u₁ and u₂ are the initial velocities of the body.
v₁ and v₂ are the final velocities of the bodies.

Q5

Does friction affect the conservation of momentum?

Yes, friction affects momentum. As friction increases, momentum decreases.

Stay tuned with BYJU’S to know more about the law of conservation of momentum, Newton’s Second Law of Motion, and much more.