The linear momentum of a particle is defined as the product of the mass of the particle times the velocity of that particle. Conservation of momentum of a particle is a property exhibited by any particle where the total amount of momentum never changes. Linear momentum of a particle is a vector quantity and is denoted by
| Table of Contents |
Conservation of Linear Momentum
According to the conservation of linear momentum,
If the net external force acting on a system of bodies is zero, then the momentum of the system remains constant.
We have to remember that the momentum of the system is conserved and not that of the individual particles. The momentum of the individual bodies in the system might increase or decrease according to the situation, but the momentum of the system will always be conserved, as long as there is no external net force acting on it.
Conservation of Linear Momentum Formula
The principle of conservation of momentum states that if two objects collide, then the total momentum before and after the collision will be the same if there is no external force acting on the colliding objects.
The conservation of linear momentum formula mathematically expresses that the momentum of the system remains constant when the net external force is zero.
Initial momentum = Final momentum
| Pi = Pf |
Linear Momentum Formula
Linear momentum is mathematically expressed as:
You may also like to learn more about other related concepts as given below:
| Related Links | |
| Angular Momentum | Linear Momentum |
| Conservation of Angular Momentum | Law of Conservation of Momentum Derivation |
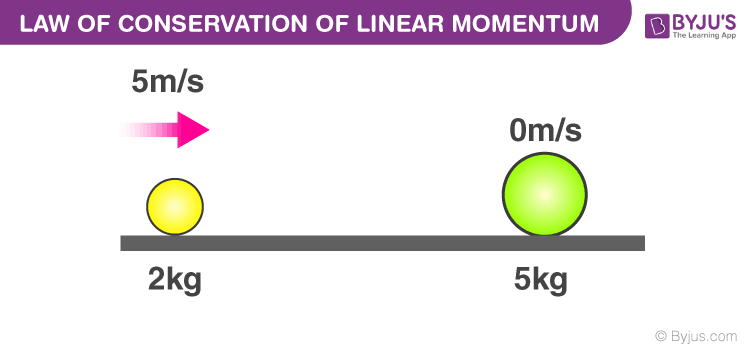
Conservation of Linear Momentum Equation
The law of conservation of momentum can be explained from the second law of motion. Newton’s second law of motion says that the rate of change of linear momentum of a body is equal to the net external force applied to it.
Mathematically it is expressed as:
If the net external force acting on a body is zero, then the rate of change of momentum is also zero, which means that there is no change in momentum.
Read More: Newton’s Second Law of Motion
Conservation of Linear Momentum Example
Two bodies of mass M and m are moving in opposite directions with the velocities v. If they collide and move together after the collision, we have to find the velocity of the system.
Since there is no external force acting on the system of two bodies, momentum will be conserved.
Initial momentum = Final momentum
(Mv – mv) = (M+m)VFinal
From this equation, we can easily find the final velocity of the system.
Conservation of Linear Momentum Applications
One of the applications of conservation of momentum is the launching of rockets. The rocket fuel burns are pushes the exhaust gases downwards, and due to this, the rocket gets pushed upwards. Motorboats also work on the same principle, it pushes the water backward and gets pushed forward in reaction to conserve momentum.
Here is a video that explains the application of PCLM using an example of a bomb explosion

Frequently Asked Questions – FAQs
Discuss the law of conservation of momentum. State its unit.
How does Newton’s second law of motion apply to rockets?
How does Newton’s second law apply to a car crash?
What is the other name for Newton’s second law?
What are some daily life examples of Newton’s second law of motion?
- Acceleration of the rocket is due to the force applied known as thrust and is an example of Newton’s second law of motion.
- Another example of Newton’s second law is when an object falls from a certain height, the acceleration increases because of the gravitational force.
Stay tuned to BYJU’S and Fall in Love with Learning!

Good app
Well explained. Simple and to the point
Nice app
excellent app, i would like to thank byju’s for providing such kinda help to students for their preparations.
good app
Awesome explanation and a very good app
Best app and best teachers ever had.
Very good explanation, I am quite satisfied with it.
Excellent app
Conservation of linear momentum is equivalent to which laws of Newton?
Conservation of linear momentum is equivalent to Newton’s Third Law of Motion.
The example questions given are very useful
Explained very briefly!! Thank you for this content, it was really helpful.