Segment and area of a segment of the circle: A segment is a part of a circle basically the region between the chord and an arc. A circle is a path traced by a point that is equidistant from a unique point on the plane, this point is called the centre of the circle and the constant distance is called the radius of the circle. A segment is an interior region of a circle. The area enclosed by a segment and the angle subtended by a segment is called a sector. The area of the segment of a circle is determined by subtracting the triangle formed inside the sector from the sector which has the segment.
In this article, we shall discuss in detail the segment and area of a segment of a circle and all related theorems with proof.
| Table of Contents: |
Segment of a Circle Definition
A segment of a circle can be defined as a region bounded by a chord and a corresponding arc lying between the chord’s endpoints. In other words, a circular segment is a region of a circle which is created by breaking apart from the rest of the circle through a secant or a chord. We can also define segments as the parts that are divided by the circle’s arc and connected through a chord by the endpoints of the arc. It is to be noted that the segments do not contain the center point.
Types of Segments in a Circle
According to the definition, the part of the circular region which is enclosed between a chord and corresponding arc is known as a segment of the circle. There are two classifications of segments in a circle, namely the major segment and the minor segment. The segment having a larger area is known as the major segment and the segment having a smaller area is known as the minor segment.

In the figure above, ADB is the major segment and ABC is the minor segment. If nothing is stated, a segment means the minor segment. In order to calculate the area of a segment of a circle, one should know how to calculate the area of the sector of the circle.
Area of a Segment of a Circle Formula
The formula to find segment area can be either in terms of radians or in terms of degree. The formulas for a circle’s segment are as follows:

Area of a Segment of a Circle Formula
| Formula To Calculate Area of a Segment of a Circle | |
|---|---|
| Area of a Segment in Radians | A = (½) × r2 (θ – Sin θ) |
| Area of a Segment in Degrees | A = (½) × r 2 × [(π/180) θ – sin θ] |
How to Calculate the Area of Segment of Circle?

Figure 1: Segment of a Circle Derivation
In fig. 1, if ∠AOB = θ (in degrees), then the area of the sector AOBC (A sector AOBC) is given by the formula;
(A sector AOBC) = θ/360° × πr2
Let the area of ΔAOB be AΔAOB. So, the area of the segment ABC(A segment ABC) is given by
(A segment ABC) = (A sector AOBC) – AΔAOB
(A segment ABC) = θ/360° × πr2 – AΔAOB

Figure 2: Calculating Area of Segment of Circle
The area of ΔAOB can be calculated in two steps, As shown in fig. 2,
Calculate the height of ΔAOB i.e. OP using Pythagoras theorem as given below:
OP = √[r2–(AB/2)2] if the length of AB is given
or, OP = r cos (θ/2), if θ is given (in degrees)
Calculate the area of ∆AOB using the formula:
(A area ΔAOB) = ½ × base × height = ½ × AB × OP
Now, substituting the values in the area of segment formula, the area can be calculated.
Related Video

Theorems on Segment of a Circle
There are two main theorems based on a circle’s segments which are:
- Alternate Segment Theorem
- Angle in the Same Segment Theorem
- Alternate Angle Theorem
Theorem 1: Inscribed Angle Theorem
Statement: The inscribed angle theorem states that an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle.
In the below figure, ∠AOC = 2∠ABC

Inscribed Angle Theorem
Proof:
Consider the alternate angle ACD (as x) is equal to the angle ABC is shown on the other side of the chord, where DC is the tangent to the circle.
Triangle ABC has points A, B and C on the circumference of a circle with centre O. Join OA and OC to form triangle AOC.
Let ∠ACD = x, and ∠OCA = y.
We know that tangent to a circle is at a right angle to the radius of a circle,
Therefore, x + y = 90° ——————————(i)
Bisect the triangle AOC from the point O, then the triangle formed is a right-angled triangle at E. Let the bisected angle be z.
Therefore, ∠AOE = ∠COE =z
Sum of angles of a triangle is 180°
In △COE, y + z + 90° = 180°
Or, y + z = 90° —————————(ii)
Equating equation (i) and (ii), we have
x = z
We know, ∠ABC = ∠ACD = x
Therefore, ∠AOC = 2z
and ∠ABC = x
Theorem 2: Angle in the Same Segment Theorem
Statement: Angles which are in the same segment are equal, i.e. angles subtended (made) by the same arc at the circumference are equal.
According to angle in the same segment theorem, angles in the same segment are equal. Consider triangle ABC and ADC having ∠ABC and ∠ADC in the major segment of a circle.
To prove: ∠ABC = ∠ADC
Construction: Join O to A and C.

Angles in Same Segment Theorem
Proof:
Let ∠AOC = x
From Theorem 1, we have
x = 2∠ABC —————–(i)
Also, x = 2∠ADC ———————-(ii)
From (i) and (ii), we have
Theorem 3: Alternate Angle Theorem
Statement: The alternate segment theorem (also known as the tangent-chord theorem) states that in any circle, the angle between a chord and a tangent through one of the endpoints of the chord is equal to the angle in the alternate segment.
In the following figure, ∠ACD = ∠ABC = x

Alternate Angle Theorem
Note: Check out more circle theorems and their converses here.
Example Question Based on Segment Formula
Question 1:
What is the area of the segment corresponding to the arc subtending an angle of 60° at the centre of a circle with radius 6 cm?
Solution:
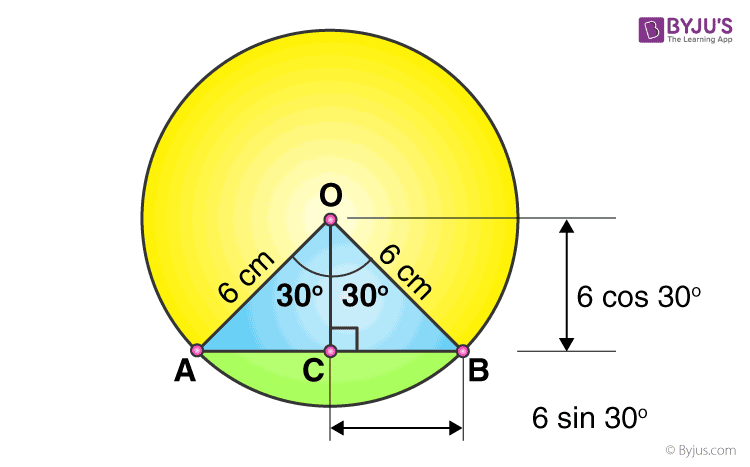
Area of the sector AOB (blue region + green region) = (θ/360°) × πr2 = (60°/360°) × π × 62 = 6π cm2
Area of ΔAOB = ½ × OC × AB
Where OC = 6 cos 30° = 6 × (√3/2) = 3√3 cm
And AB = 2BC = 2 × 6 sin 30° = 2 × 6 × ½ = 6 cm
Substituting the values, Area of ∆AOB = ½ × 3√3 × 6 = 9√3 cm2
So, area of segment AB = 6π cm2 – 9√3 cm2
= 3(2π – 3√3) cm2
More Topics Related to Circles and Its Segment
| Parts of a Circle | Properties of Circle |
| Circumference of a Circle | Radius Of A Circle |
| Chord Of A Circle And Its Theorem | Area Of a Circle |
| Circles Class 10 Notes: Chapter 10 | Circles Class 9 |
Practice Questions
- A chord of a circle of radius 14 cm makes a right angle at the centre. Find the areas of the major and minor segments of the circles formed.
- Find the area of both the segments cut off by a chord of length 10 cm of a circle whose radius is 5√2 cm.
- A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor and major segments.
Frequently Asked Questions
What is a Circle?
A circle can be defined as a closed two-dimensional figure in which all the points in the boundary are equidistant from a single point called the centre.
What is the Segment of a Circle?
A segment of a circle can be defined as the region which is created by a secant or a chord with the corresponding arc of the circle. The segment portraying a larger area is known as the major segment and the segment having a smaller area is known as a minor segment.
What is the Formula for the Area of a Segment?
The area of a segment can be calculated in radians using the following formula:
A = (½) × r2 (θ – Sin θ)
Is a Semicircle a Segment?
Yes, semicircle can be termed as a segment. It is the biggest segment of a circle. Also, for a semicircle, the diameter divides the circle the area covered by the sector is also the area covered by the segment.
How do you calculate area of segment if you know the length of the chord but not the size of any angles in triangle?
If the radius and the segment height of a circle are given, then the formula to calculate the area of the segment is
Area of Segment = r^2 cos^-1[(r-h)/r]-(r-h)√[2rh -h^2]
At least two dimensions must be known. Draw a perpendicular to the base passing through apex. It will form a right angled triangle. Using Pythagoras’s theorem you can calculate other unknown dimension. Using trigonometric formulae you can calculate other angles of the triangle.
Send me a formula of minor segment
Area of segment = Area of sector – Area of Triangle
= (θ/360° × πr^2) – Area of triangle