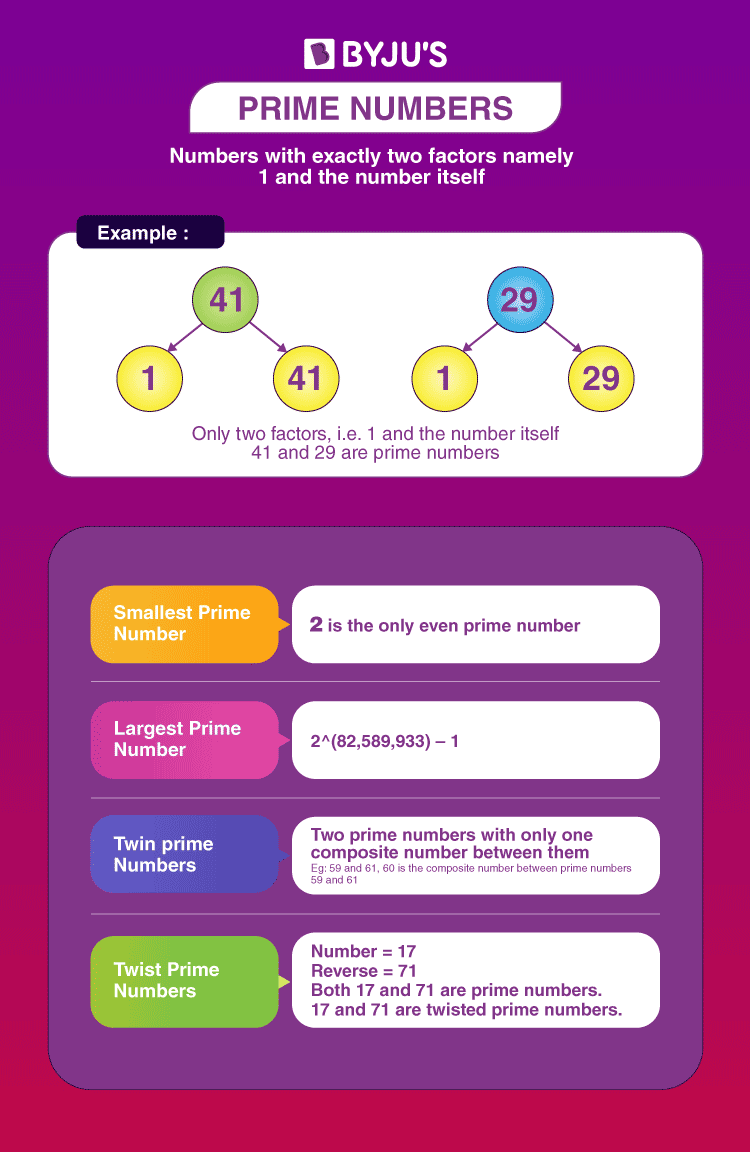
Prime numbers are natural numbers that are divisible by only 1 and the number itself. In other words, prime numbers are positive integers greater than 1 with exactly two factors, 1 and the number itself. Some of the prime numbers include 2, 3, 5, 7, 11, 13, etc. Always remember that 1 is neither prime nor composite. Also, we can say that except for 1, the remaining numbers are classified as prime and composite numbers. All prime numbers are odd numbers except 2, 2 is the smallest prime number and is the only even prime number.
Prime numbers are the natural numbers greater than 1 with exactly two factors, i.e. 1 and the number itself.
In this article, you will learn the meaning and definition of prime numbers, their history, properties, list of prime numbers from 1 to 1000, chart, differences between prime numbers and composite numbers, how to find the prime numbers using formulas, along with video lesson and examples.
Learn: Mathematics
| Table of Contents: |
What are Prime Numbers?
A prime number is a positive integer having exactly two factors, i.e. 1 and the number itself. If p is a prime, then its only factors are necessarily 1 and p itself. Any number that does not follow this is termed a composite number, which can be factored into other positive integers. Another way of defining it is a positive number or integer, which is not a product of any other two positive integers other than 1 and the number itself.
First Ten Prime Numbers
The first ten primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Note: It should be noted that 1 is a non-prime number. It is a unique number.
Download PDF – Prime Numbers
| Click here to download the PDF of Prime numbers:- |
Download PDF |
History of Prime Numbers
The prime number was discovered by Eratosthenes (275-194 B.C., Greece). He took the example of a sieve to filter out the prime numbers from a list of natural numbers and drain out the composite numbers.
Students can practise this method by writing the positive integers from 1 to 100, circling the prime numbers, and putting a cross mark on composites. This kind of activity refers to the Sieve of Eratosthenes.
Properties of Prime Numbers
Some of the properties of prime numbers are listed below:
- Every number greater than 1 can be divided by at least one prime number.
- Every even positive integer greater than 2 can be expressed as the sum of two primes.
- Except 2, all other prime numbers are odd. In other words, we can say that 2 is the only even prime number.
- Two prime numbers are always coprime to each other.
- Each composite number can be factored into prime factors and individually all of these are unique in nature.
Prime Numbers Chart
Before calculators and computers, numerical tables were used for recording all of the primes or prime factorizations up to a specified limit and are usually printed. The most beloved method for producing a list of prime numbers is called the sieve of Eratosthenes. This method results in a chart called Eratosthenes chart, as given below. The chart below shows the prime numbers up to 100, represented in coloured boxes.
Video Lesson on Prime Numbers
A prime number is a whole number greater than 1 whose only factors are 1 and itself. The first ten primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. It should be noted that 1 is a non-prime number. Conferring to the definition of prime number, which states that a number should have exactly two factors, but number 1 has one and only one factor. Thus 1 is not considered a Prime number.
To learn more about prime numbers watch the video given below.

List of Prime Numbers 1 to 100
There are several primes in the number system. As we know, the prime numbers are the numbers that have only two factors which are 1 and the number itself.
The list of prime numbers from 1 to 100 are given below:
| Prime Numbers between 1 and 100 | |
| Prime numbers between 1 and 10 | 2, 3, 5, 7 |
| Prime numbers between 10 and 20 | 11, 13, 17, 19 |
| Prime numbers between 20 and 30 | 23, 29 |
| Prime numbers between 30 and 40 | 31, 37 |
| Prime numbers between 40 and 50 | 41, 43, 47 |
| Prime numbers between 50 and 60 | 53, 59 |
| Prime numbers between 60 and 70 | 61, 67 |
| Prime numbers between 70 and 80 | 71, 73, 79 |
| Prime numbers between 80 and 90 | 83, 89 |
| Prime numbers between 90 and 100 | 97 |
Thus, there are 25 prime numbers between 1 and 100, i.e. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97. All these numbers are divisible by only 1 and the number itself. Hence, these numbers are called prime numbers. Also, these are the first 25 prime numbers.
Prime Numbers 1 to 200
Here is the list of prime numbers from 1 to 200, which we can learn and crosscheck if there are any other factors for them.
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199 |
Prime Numbers 1 to 1000
There are a total of 168 prime numbers between 1 to 1000. They are:
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997. |
Also, get the list of prime numbers from 1 to 1000 along with detailed factors here.
Facts About Prime Numbers
The table below shows the important points about prime numbers. These will help you to solve many problems in mathematics.
| Smallest Prime Number | 2 |
| Largest Prime Number | As of November 2022, the largest known prime number is 282,589,933 – 1, with 24,862,048 digits.
It was founded by the Great Internet Mersenne Prime Search (GIMPS) in 2018. |
| Even Prime Number | 2 is the only even prime number, and the rest of the prime numbers are odd numbers, hence called odd prime numbers. |
| Twin Prime numbers | The prime numbers with only one composite number between them are called twin prime numbers or twin primes. The other definition of twin prime numbers is the pair of prime numbers that differ by 2 only. For example, 3 and 5 are twin primes because 5 – 3 = 2.
The other examples of twin prime numbers are:
|
| Coprime numbers | Two numbers are called coprime to each other if their highest common factor is 1. Prime numbers and coprime numbers are not the same. For example, 6 and 13 are coprime because the common factor is 1 only. |
Click here to learn more about twin prime numbers.
How to Find Prime Numbers?
The following two methods will help you to find whether the given number is a prime or not.
Method 1:
We know that 2 is the only even prime number. And only two consecutive natural numbers which are prime are 2 and 3. Apart from those, every prime number can be written in the form of 6n + 1 or 6n – 1 (except the multiples of prime numbers, i.e. 2, 3, 5, 7, 11), where n is a natural number.
For example:
6(1) – 1 = 5
6(1) + 1 = 7
6(2) – 1 = 11
6(2) + 1 = 13
6(3) – 1 = 17
6(3) + 1 = 19
6(4) – 1 = 23
6(4) + 1 = 25 (multiple of 5)
…
Method 2:
To know the prime numbers greater than 40, the below formula can be used.
n2 + n + 41, where n = 0, 1, 2, ….., 39
For example:
(0)2 + 0 + 0 = 41
(1)2 + 1 + 41 = 43
(2)2 + 2 + 41 = 47
…..
Is 1 a Prime Number?
Conferring to the definition of the prime number, which states that a number should have exactly two factors for it to be considered a prime number. But, number 1 has one and only one factor which is 1 itself. Thus, 1 is not considered a Prime number.
Examples: 2, 3, 5, 7, 11, etc.
In all the positive integers given above, all are either divisible by 1 or itself, i.e. precisely two positive integers.
| Related questions on Prime numbers: |
Prime Numbers vs Composite Numbers
A few differences between prime numbers and composite numbers are tabulated below:
| Prime Numbers | Composite Numbers |
| A prime number has two factors only. | A composite number has more than two factors. |
| It can be divided by 1 and the number itself.
For example, 2 is divisible by 1 and 2. |
It can be divided by all its factors. For example, 6 is divisible by 2,3 and 6. |
| Examples: 2, 3, 7, 11, 109, 113, 181, 191, etc. | Examples: 4, 8, 10, 15, 85, 114, 184, etc. |
Prime Numbers Related Articles
Solved Examples on Prime Numbers
Example 1:
Is 10 a Prime Number?
Solution:
No, because it can be divided evenly by 2 or 5, 2×5=10, as well as by 1 and 10.
Alternatively,
Using method 1, let us write in the form of 6n ± 1.
10 = 6(1) + 4 = 6(2) – 2
This is not of the form 6n + 1 or 6n – 1.
Hence, 10 is not a prime number.
Example 2:
Is 19 a Prime Number?
Solution:
Let us write the given number in the form of 6n ± 1.
6(3) + 1 = 18 + 1 = 19
Therefore, 19 is a prime number.
Example 3:
Find if 53 is a prime number or not.
Solution:
The only factors of 53 are 1 and 53.
Or
Let us write the given number in the form of 6n ± 1.
6(9) – 1 = 54 – 1 = 53
So, 53 is a prime number.
Example 4:
Check if 64 is a prime number or not.
Solution:
The factors of 64 are 1, 2, 4, 8, 16, 32, 64.
It has factors other than 1 and 64.
Hence, it is a composite number and not a prime number.
Example 5:
Which is the greatest prime number between 1 to 10?
Solution:
As we know, the first 5 prime numbers are 2, 3, 5, 7, 11.
There are 4 prime numbers between 1 and 10 and the greatest prime number between 1 and 10 is 7.
Practice Problems
- Identify the prime numbers from the following numbers:
34, 27, 29, 41, 67, 83 - Which of the following is not a prime number?
2, 19, 91, 57 - Write the prime numbers less than 50.
Keep visiting BYJU’S to get more such Maths articles explained in an easy and concise way. Also, register now and get access to 1000+ hours of video lessons on different topics.
Frequently Asked Questions on Prime Numbers
What are Prime Numbers in Maths?
How to find prime numbers?
To find whether a number is prime, try dividing it with the prime numbers 2, 3, 5, 7 and 11. If the number is exactly divisible by any of these numbers, it is not a prime number, otherwise, it is a prime. Alternatively, we can find the prime numbers by writing their factors since a prime number has exactly two factors, 1 and the number itself.
What are the examples of prime numbers?
As we know, prime numbers are whole numbers greater than 1 with exactly two factors, i.e. 1 and the number itself. Some of the examples of prime numbers are 11, 23, 31, 53, 89, 179, 227, etc.
What is the smallest prime number?
2 is the smallest prime number. Also, it is the only even prime number in maths.
What is the largest prime number so far?
Which is the largest 4 digit prime number?
The largest 4 digits prime number is 9973, which has only two factors namely 1 and the number itself.
What are prime numbers between 1 and 50?
The list of prime numbers between 1 and 50 are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47
Why 1 is not a prime number?
As per the definition of prime numbers, 1 is not considered as the prime number since a prime number is a natural number greater than 1 that is not a product of two smaller natural numbers.


By just helped me understand prime numbers in a better way. I have learnt many concepts in mathematics and science in a very easy and understanding way
Yes
I understand I lot by this website about prime numbers
when are classes mam or sir.
thank you.
from: lakshita singh.
have a good day.
This is a very nice app .,i understand many more things on this app .thankyou so much teachers 🙏🙏🙏
Thanks for video I learn a lot by watching this website