NCERT Solutions for Class 7 Maths Chapter 10 Practical Geometry

*According to the latest CBSE Syllabus 2023-24, this chapter has been removed.

NCERT Solutions for Class 7 Maths Chapter 10 Practical Geometry download the PDF are given below. The foremost objective is to help students understand and crack these problems. We at BYJU’S, have prepared the NCERT Solutions for Class 7 Maths and solved them step-by-step with complete descriptions.

There are 5 exercises present in Chapter 10 – Practical Geometry of NCERT Solutions for Class 7 Maths. The concepts covered in this chapter include

• Construction of a Line Parallel to a Given Line, through a Point Not on the Line
• Construction of Triangle
• Constructing a Triangle When the Lengths of Its Three Sides Are Known (SSS Criterion)
• Constructing a Triangle When the Lengths of Two Sides and the Measure of the Angle between Them Are Known (SAS Criterion)
• Constructing a Triangle When The Measures of Two of Its Angles and the Length of the Side Inclined between Them Is Given (ASA Criterion)
• Constructing a Right-Angled Triangle When the Length of One Leg and Its Hypotenuse Are Given (RHS Criterion)

NCERT Solutions for Class 7 Maths Chapter 10 Practical Geometry

Download PDF

carouselExampleControls112

Previous





Next

Access Exercises of NCERT Solutions for Class 7 Maths Chapter 10 Practical Geometry

Exercise 10.1 Solutions

Exercise 10.2 Solutions

Exercise 10.3 Solutions

Exercise 10.4 Solutions

Exercise 10.5 Solutions

Access Answers to NCERT Class 7 Maths Chapter 10 – Practical Geometry

Exercise 10.1 Page: 196

1. Draw a line, say AB, take a point C outside it. Through C, draw a line parallel to AB using ruler and compasses only.

Solution:-

Steps for construction

1. Draw a line AB.

2. Take any point Q on AB and a point P outside AB and join PQ.

3. With Q as the centre and any radius, draw an arc to cut AB at E and PQ at F.

4. With P as the centre and the same radius, draw an arc IJ to cut QP at G.

5. Place the pointed tip of the compass at E and adjust the opening so that the pencil tip is at F.

6. With the same opening as in step 5 and with G as the centre, draw an arc cutting the arc IJ at H.

7. Now, join PH to draw a line CD.

2. Draw a line L. Draw a perpendicular to L at any point on L. On this perpendicular, choose a point X, 4 cm away from l. Through X, draw a line m parallel to L.

Solution:-

Steps for construction

1. Draw a line L.

2. Take any point P on line L.

3. At point P, draw a perpendicular line N.

4. Place the pointed tip of the compass at P and adjust the compass up to length of 4 cm, draw an arc to cut this perpendicular at point X.

5. At point X, again draw a perpendicular line M.

3. Let L be a line and P be a point not on L. Through P, draw a line m parallel to L. Now join P to any point Q on L. Choose any other point R on m. Through R, draw a line parallel to PQ. Let this meet L at S. What shape do the two sets of parallel lines enclose?

Solution:-

Steps for construction

1. Draw a line L.

2. Take any point Q on L and a point P outside L and join PQ.

3. Make sure that angles at point P and point Q are equal, i.e., ∠Q = ∠P

4. At point P, extend the line to get line M which is parallel L.

5. Then take any point R on line M.

6. At point R, draw an angle such that ∠P = ∠R.

7. At point R, extend the line which intersects line L at S and draw a line RS.

Exercise 10.2 Page: 199

1. Construct ΔXYZ in which XY = 4.5 cm, YZ = 5 cm and ZX = 6 cm.

Solution:-

Steps of construction

1. Draw a line segment YZ = 5 cm.

2. With Z as a centre and radius 6 cm, draw an arc.

3. With Y as a centre and radius 4.5 cm, draw another arc, cutting the previous arc at X.

4. Join XY and XZ.

Then, ΔXYZ is the required triangle.

2. Construct an equilateral triangle of side 5.5 cm.

Solution:-

Steps of construction

1. Draw a line segment AB = 5.5 cm.

2. With A as a centre and radius 5.5 cm, draw an arc.

3. With B as a centre and radius 5.5 cm, draw another arc, cutting the previous arc at C.

4. Join CA and CB.

Then, ΔABC is the required equilateral triangle.

3. Draw ΔPQR with PQ = 4 cm, QR = 3.5 cm and PR = 4 cm. What type of triangle is this?

Solution:-

Steps of construction

1. Draw a line segment QR = 3.5 cm.

2. With Q as a centre and radius 4 cm, draw an arc.

3. With R as a centre and radius 4 cm, draw another arc, cutting the previous arc at P.

4. Join PQ and PR.

Then, ΔPQR is the required isosceles triangle.

4. Construct ΔABC, such that AB = 2.5 cm, BC = 6 cm and AC = 6.5 cm. Measure ∠B.

Solution:-

1. Draw a line segment BC = 6 cm.

2. With B as a centre and radius 2.5 cm, draw an arc.

3. With C as a centre and radius 6.5 cm, draw another arc, cutting the previous arc at A.

4. Join AB and AC.

Then, ΔABC is the required triangle.

5. When we will measure the angle B of triangle by a protractor, the angle is equal to ∠B = 90^o

Exercise 10.3 Page: 200

1. Construct ΔDEF such that DE = 5 cm, DF = 3 cm and m∠EDF = 90^o.

Solution:-

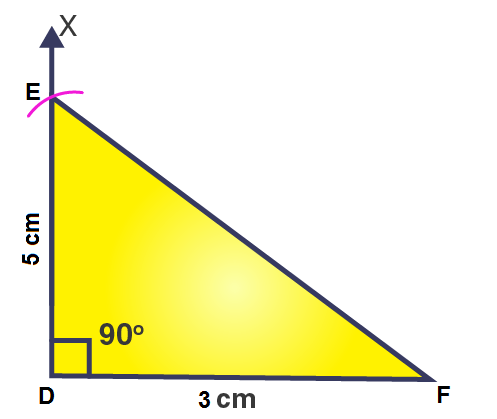
Steps of construction

1. Draw a line segment DF = 3 cm.

2. At point D, draw a ray DX to making an angle of 90^o, i.e., ∠XDF = 90^o.

3. Along DX, set off DE = 5cm.

4. Join EF.

Then, ΔEDF is the required right-angled triangle.

2. Construct an isosceles triangle in which the lengths of each of its equal sides is 6.5 cm and the angle between them is 110^o.

Solution:-

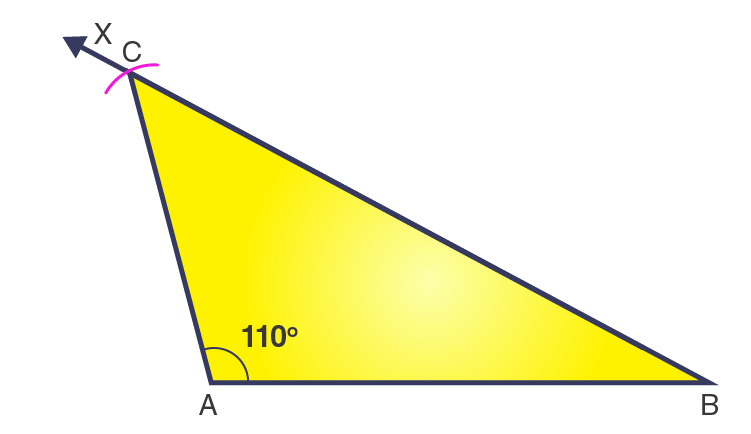
Steps of construction

1. Draw a line segment AB = 6.5 cm.

2. At point A, draw a ray AX to making an angle of 110^o, i.e., ∠XAB = 110^o.

3. Along AX, set off AC = 6.5cm.

4. Join CB.

Then, ΔABC is the required isosceles triangle.

3. Construct ΔABC with BC = 7.5 cm, AC = 5 cm and m∠C = 60°.

Solution:-

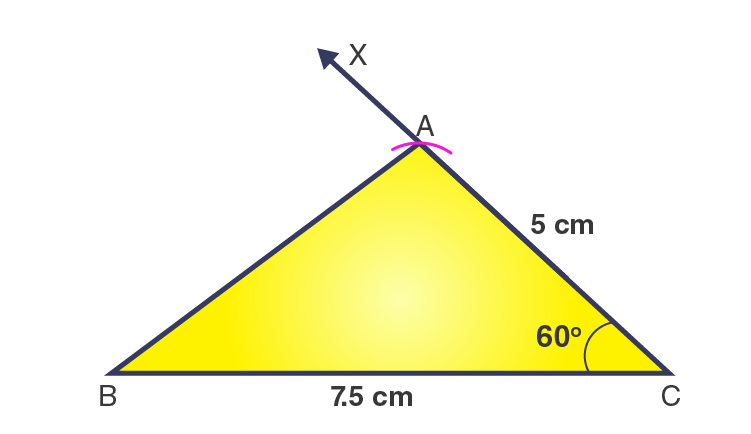
Steps of construction

1. Draw a line segment BC = 7.5 cm.

2. At point C, draw a ray CX to making an angle of 60^o, i.e., ∠XCB = 60^o.

3. Along CX, set off AC = 5cm.

4. Join AB.

Then, ΔABC is the required triangle.

Exercise 10.4 Page: 202

1. Construct ΔABC, given m ∠A =60^o, m ∠B = 30^o and AB = 5.8 cm.

Solution:-

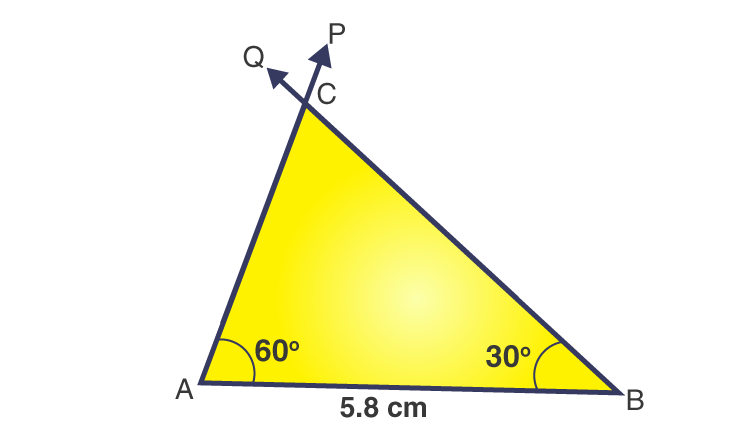
Steps of construction:

1. Draw a line segment AB = 5.8 cm.

2. At point A, draw a ray P to making an angle of 60^o, i.e., ∠PAB = 60^o.

3. At point B, draw a ray Q to making an angle of 30^o, i.e., ∠QBA = 30^o.

4. Now, the two rays – AP and BQ – intersect at point C.

Then, ΔABC is the required triangle.

2. Construct ΔPQR if PQ = 5 cm, m∠PQR = 105^o and m∠QRP = 40^o.

(Hint: Recall angle-sum property of a triangle).

Solution:-

We know that the sum of the angles of a triangle is 180^o.

∴ ∠PQR + ∠QRP + ∠RPQ = 180^o

= 105^o+ 40^o+ ∠RPQ = 180^o

= 145^o + ∠RPQ = 180^o

= ∠RPQ = 180^o– 145⁰

= ∠RPQ = 35^o

Hence, the measures of ∠RPQ is 35^o.

Steps of construction

1. Draw a line segment PQ = 5 cm.

2. At point P, draw a ray L to making an angle of 105^o, i.e., ∠LPQ = 35^o.

3. At point Q, draw a ray M to making an angle of 40^o, i.e., ∠MQP = 105^o.

4. Now, the two rays – PL and QM – intersect at point R.

Then, ΔPQR is the required triangle.

3. Examine whether you can construct ΔDEF, such that EF = 7.2 cm, m∠E = 110° and m∠F = 80°. Justify your answer.

Solution:-

From the question, it is given that

EF = 7.2 cm

∠E = 110^o

∠F = 80^o

Now, we have to check whether it is possible to construct ΔDEF from the given values.

We know that the sum of the angles of a triangle is 180^o.

Then,

∠D + ∠E + ∠F = 180^o

∠D + 110^o+ 80^o= 180^o

∠D + 190^o = 180^o

∠D = 180^o– 190⁰

∠D = -10^o

We may observe that the sum of two angles is 190^o is greater than 180^o. So, it is not possible to construct a triangle.

Exercise 10.5 Page: 203

1. Construct the right-angled ΔPQR, where m∠Q = 90°, QR = 8cm and PR = 10 cm.

Solution:-

Steps of construction

1. Draw a line segment QR = 8 cm.

2. At point Q, draw a ray QY to making an angle of 90^o, i.e., ∠YQR = 90^o.

3. With R as a centre and radius 10 cm, draw an arc that cuts the ray QY at P.

4. Join PR.

Then, ΔPQR is the required right-angled triangle.

2. Construct a right-angled triangle whose hypotenuse is 6 cm long and one of the legs is 4 cm long

Solution:-

Let us consider ΔABC is a right-angled triangle at ∠B = 90^o

Then,

AC is hypotenuse = 6 cm … [Given in the question]

BC = 4 cm

Now, we have to construct the right-angled triangle by using the above values.

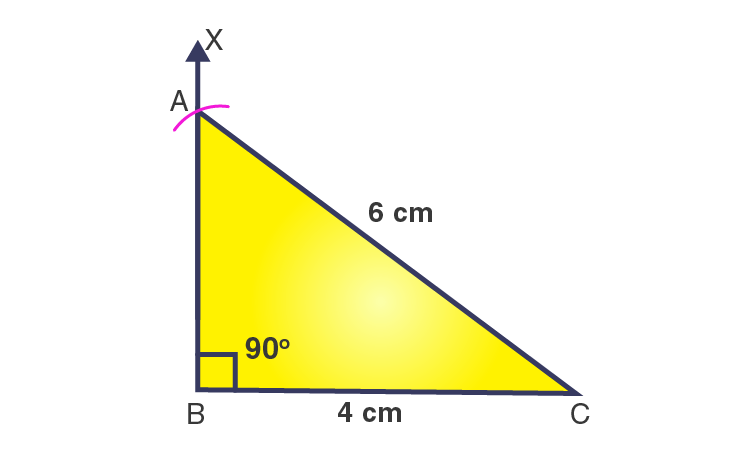
Steps of construction

1. Draw a line segment BC = 4 cm.

2. At point B, draw a ray BX to making an angle of 90^o, i.e., ∠XBC = 90^o.

3. With C as a centre and radius 6 cm, draw an arc that cuts the ray BX at A.

4. Join AC.

Then, ΔABC is the required right-angled triangle.

3. Construct an isosceles right-angled triangle ABC, where m∠ACB = 90° and AC = 6 cm.

Solution:-

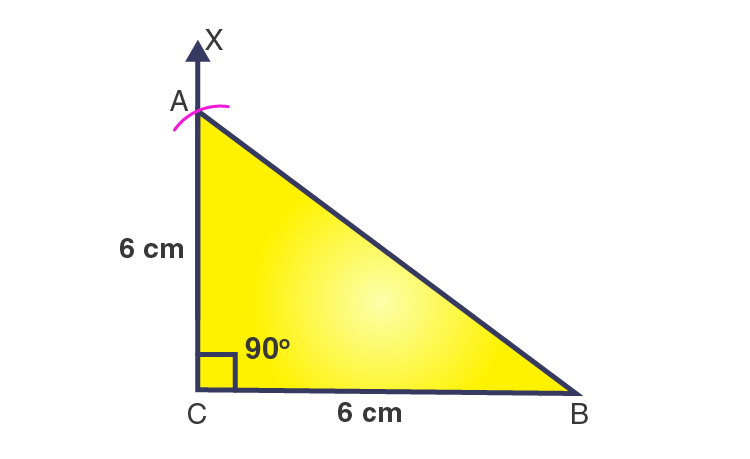
Steps of construction

1. Draw a line segment BC = 6 cm.

2. At point C, draw a ray CX to making an angle of 90^o, i.e., ∠XCB = 90^o.

3. With C as a centre and radius 6 cm, draw an arc that cuts the ray CX at A.

4. Join AB.

Then, ΔABC is the required right-angled triangle.

Disclaimer:

Dropped Topics- 10.1 Introduction, 10.2 Construction of a line parallel to a given line, through a point not on the line, 10.3 Construction of triangles, 10.4 Constructing a triangle when lengths of its three sides are known (SSS criterion), 10.5 Constructing a triangle when the lengths of two sides and the measure of the angle between them are known (SAS criterion), 10.6 Constructing a triangle when the measures of two of its angles and the length of the side included between them is given (ASA criterion),
10.7 Constructing a right-angled triangle when the length of one leg and its hypotenuse are given (RHS criterion).