NCERT Solutions Class 10 Maths Chapter 4 – Quadratic Equations Exercise 4.3 contain all the solutions to the Maths problems provided in the textbook, page number 87. The questions from every section are framed and solved accurately by the subject experts. The stepwise solutions to all the questions have been explained here. NCERT Solutions Class 10 Chapter 4 – Quadratic Equations is an important chapter and requires conceptual knowledge.
The exercises provided in the solutions should be dealt with thoroughly to score well in the examinations. NCERT Solutions Class 10 Maths covers all the topics along with the solved questions and exercises for practice. Maths requires a good understanding of the topic and a lot of practice. The tips and tricks to solve the questions in the exercises are provided in the Class 10 Maths NCERT Solutions.
NCERT Solutions for Class 10 Maths Chapter 4 – Quadratic Equations Exercise 4.3 provides easy ways to calculate the unknown values of x. NCERT Solutions are the best way to evaluate yourself. Students are advised to practise the exercises repeatedly to overcome their imperfections. This will help in getting correct answers in a very short time.
NCERT Solutions for Class 10 Maths Chapter 4 – Quadratic Equations Exercise 4.3
Access other exercise solutions of Class 10 Maths Chapter 4 – Quadratic Equations
Exercise 4.1 Solutions– 2 Questions
Exercise 4.2 Solutions– 6 Questions
Exercise 4.4 Solutions– 5 Questions
Access Answers of Maths NCERT Class 10 Chapter 4- Quadratic Equations Exercise 4.3
1. Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
(i) 2x2 – 7x +3 = 0
(ii) 2x2 + x – 4 = 0
(iii) 4x2 + 4√3x + 3 = 0
(iv) 2x2 + x + 4 = 0
Solutions:
(i) 2x2 – 7x + 3 = 0
⇒ 2x2 – 7x = – 3
Dividing by 2, on both sides, we get,
⇒ x2 -7x/2 = -3/2
⇒ x2 -2 × x ×7/4 = -3/2
On adding (7/4)2 to both sides of the equation, we get,
⇒ (x)2-2×x×7/4 +(7/4)2 = (7/4)2-3/2
⇒ (x-7/4)2 = (49/16) – (3/2)
⇒(x-7/4)2 = 25/16
⇒(x-7/4)2 = ±5/4
⇒ x = 7/4 ± 5/4
⇒ x = 7/4 + 5/4 or x = 7/4 – 5/4
⇒ x = 12/4 or x = 2/4
⇒ x = 3 or x = 1/2
(ii) 2x2 + x – 4 = 0
⇒ 2x2 + x = 4
Dividing both sides of the equation by 2, we get,
⇒ x2 +x/2 = 2
Now on adding (1/4)2Â to both sides of the equation, we get,
⇒ (x)2 + 2 × x × 1/4 + (1/4)2 = 2 + (1/4)2
⇒ (x + 1/4)2 = 33/16
⇒ x + 1/4 = ± √33/4
⇒ x = ± √33/4 – 1/4
⇒ x = (± √33-1)/4
Therefore, either x = (√33-1)/4 or x = (-√33-1)/4
(iii) 4x2 + 4√3x + 3 = 0
Converting the equation into a2+2ab+b2 form, we get,
⇒ (2x)2 + 2 × 2x × √3 + (√3)2 = 0
⇒ (2x + √3)2 = 0
⇒ (2x + √3) = 0 and (2x + √3) = 0
Therefore, either x = -√3/2 or x = -√3/2.
(iv) 2x2 + x + 4 = 0
⇒ 2x2 + x = -4
Dividing both sides of the equation by 2, we get
⇒ x2 + 1/2x = 2
⇒ x2 + 2 × x × 1/4 = -2
By adding (1/4)2Â to both sides of the equation, we get
⇒ (x)2 + 2 × x × 1/4 + (1/4)2 = (1/4)2 – 2
⇒ (x + 1/4)2 = 1/16 – 2
⇒ (x + 1/4)2 = -31/16
As we know, the square of numbers cannot be negative.
Therefore, there is no real root for the given equation, 2x2 + x + 4 = 0.
2. Find the roots of the quadratic equations given in Q.1 above by applying the quadratic formula.
(i) 2x2 – 7x + 3 = 0
On comparing the given equation with ax2 + bx + c = 0, we get,
a = 2, b = -7 and c = 3
By using the quadratic formula, we get,
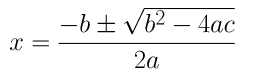
⇒ x = (7±√(49 – 24))/4
⇒ x = (7±√25)/4
⇒ x = (7±5)/4
⇒ x = (7+5)/4 or x = (7-5)/4
⇒ x = 12/4 or 2/4
∴  x = 3 or 1/2
(ii) 2x2 + x – 4 = 0
On comparing the given equation with ax2 + bx + c = 0, we get,
a = 2, b = 1 and c = -4
By using the quadratic formula, we get,
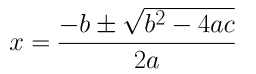
⇒x = (-1±√1+32)/4
⇒x = (-1±√33)/4
∴ x = (-1+√33)/4 or x = (-1-√33)/4
(iii) 4x2 + 4√3x + 3 = 0
On comparing the given equation with ax2 + bx + c = 0, we get,
a = 4, b = 4√3 and c = 3
By using the quadratic formula, we get,
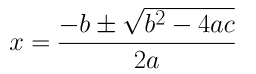
⇒ x = (-4√3±√48-48)/8
⇒ x = (-4√3±0)/8
∴ x = -√3/2 or x = -√3/2
(iv) 2x2 + x + 4 = 0
On comparing the given equation with ax2 + bx + c = 0, we get,
a = 2, b = 1 and c = 4
By using the quadratic formula, we get
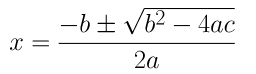
⇒ x = (-1±√1-32)/4
⇒ x = (-1±√-31)/4
As we know, the square of a number can never be negative. Therefore, there is no real solution for the given equation.
3. Find the roots of the following equations:
(i) x-1/x = 3, x ≠0
(ii) 1/x+4 – 1/x-7 = 11/30, x = -4, 7
Solution:
(i) x-1/x = 3
⇒ x2 – 3x -1 = 0
On comparing the given equation with ax2 + bx + c = 0, we get
a = 1, b = -3 and c = -1
By using the quadratic formula, we get
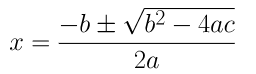
⇒ x = (3±√9+4)/2
⇒ x = (3±√13)/2
∴ x = (3+√13)/2 or x = (3-√13)/2
(ii) 1/x+4 – 1/x-7 = 11/30
⇒ x-7-x-4/(x+4)(x-7) = 11/30
⇒ -11/(x+4)(x-7) = 11/30
⇒ (x+4)(x-7) = -30
⇒ x2 – 3x – 28 = 30
⇒ x2 – 3x + 2 = 0
We can solve this equation by factorisation method now,
⇒ x2 – 2x – x + 2 = 0
⇒ x(x – 2) – 1(x – 2) = 0
⇒ (x – 2)(x – 1) = 0
⇒ x = 1 or 2
4. The sum of the reciprocals of Rehman’s ages (in years) 3 years ago and 5 years from now is 1/3. Find his present age.
Solution:
Let us say the present age of Rehman is x years.
Three years ago, Rehman’s age was (x – 3) years.
Five years after, his age will be (x + 5) years.
Given, the sum of the reciprocals of Rehman’s ages 3 years ago and after 5 years is equal to 1/3.
∴ 1/x-3 + 1/x-5 = 1/3
(x+5+x-3)/(x-3)(x+5) = 1/3
(2x+2)/(x-3)(x+5) = 1/3
⇒ 3(2x + 2) = (x-3)(x+5)
⇒ 6x + 6 = x2 + 2x – 15
⇒ x2 – 4x – 21 = 0
⇒ x2 – 7x + 3x – 21 = 0
⇒ x(x – 7) + 3(x – 7) = 0
⇒ (x – 7)(x + 3) = 0
⇒ x = 7, -3
As we know, age cannot be negative.
Therefore, Rehman’s present age is 7 years.
5. In a class test, the sum of Shefali’s marks in Mathematics and English is 30. If she had got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
Solution:
Let us say the marks of Shefali in Maths be x.
Then, the marks in English will be 30 – x.
As per the given question,
(x + 2)(30 – x – 3) = 210
(x + 2)(27 – x) = 210
⇒ -x2 + 25x + 54 = 210
⇒ x2 – 25x + 156 = 0
⇒ x2 – 12x – 13x + 156 = 0
⇒ x(x – 12) -13(x – 12) = 0
⇒ (x – 12)(x – 13) = 0
⇒ x = 12, 13
Therefore, if the marks in Maths are 12, then marks in English will be 30 – 12 = 18, and if the marks in Maths are 13, then marks in English will be 30 – 13 = 17.
6. The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Solution:
Let us say the shorter side of the rectangle is x m.
Then, larger side of the rectangle = (x + 30) m
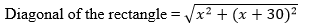
As given, the length of the diagonal is = x + 30 m
Therefore,
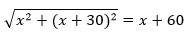
⇒ x2 + (x + 30)2 = (x + 60)2
⇒ x2 + x2 + 900 + 60x = x2 + 3600 + 120x
⇒ x2 – 60x – 2700 = 0
⇒ x2 – 90x + 30x – 2700 = 0
⇒ x(x – 90) + 30(x -90) = 0
⇒ (x – 90)(x + 30) = 0
⇒ x = 90, -30
However, the side of the field cannot be negative. Therefore, the length of the shorter side will be 90 m, and the length of the larger side will be (90 + 30) m = 120 m.
7. The difference between the squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Solution:
Let us say the larger and smaller number be x and y, respectively.
As per the question given,
x2 – y2 = 180 and y2 = 8x
⇒ x2 – 8x = 180
⇒ x2 – 8x – 180 = 0
⇒ x2 – 18x + 10x – 180 = 0
⇒ x(x – 18) +10(x – 18) = 0
⇒ (x – 18)(x + 10) = 0
⇒ x = 18, -10
The larger number will be 18 only.
x = 18
∴ y2 = 8x = 8 × 18 = 144
⇒ y = ±√144 = ±12
∴ Smaller number = ±12
Therefore, the numbers are 18 and 12 or 18 and -12.
8. A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:
It is given that
Distance = 360 km
Consider x as the speed, then the time taken
t = 360/x
If the speed is increased by 5 km/h speed will be (x + 5) km/h
Distance will be the same
t = 360/(x + 5)
We know that
Time with original speed – Time with increased speed = 1
360/x – 360/(x + 5) = 1
LCM = x (x + 5)
[360 (x + 5) – 360x]/x(x + 5) = 1360 x + 1800 – 360x = x (x + 5)
x2 + 5x = 1800
x2 + 5x – 1800 = 0
x2 + 45x – 40x – 1800 = 0
x (x + 45) – 40 (x + 45) = 0
(x – 40) (x + 45) = 0
x = 40 km/hr
As we know, the value of speed cannot be negative.
Therefore, the speed of the train is 40 km/h.
9. Two water taps together can fill a tank in
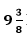hours. The tap of the larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time at which each tap can separately fill the tank.
Solution:
Let the time taken by the smaller pipe to fill the tank = x hr.
Time taken by the larger pipe = (x – 10) hr
Part of the tank filled by smaller pipe in 1 hour = 1/x
Part of the tank filled by larger pipe in 1 hour = 1/(x – 10)
As given, the tank can be filled in
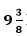 = 75/8 hours by both the pipes together.
Therefore,
1/x + 1/x-10 = 8/75
x-10+x/x(x-10) = 8/75
⇒ 2x-10/x(x-10) = 8/75
⇒ 75(2x – 10) = 8x2 – 80x
⇒ 150x – 750 = 8x2 – 80x
⇒ 8x2 – 230x +750 = 0
⇒ 8x2 – 200x – 30x + 750 = 0
⇒ 8x(x – 25) -30(x – 25) = 0
⇒ (x – 25)(8x -30) = 0
⇒ x = 25, 30/8
Time taken by the smaller pipe cannot be 30/8Â = 3.75 hours, as the time taken by the larger pipe will become negative, which is logically not possible.
Therefore, the time taken individually by the smaller pipe and the larger pipe will be 25 and 25 – 10 =15 hours, respectively.
10. An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
Solution:
Let us say, the average speed of the passenger train =  x km/h.
Average speed of express train = (x + 11) km/h
Given, the time taken by the express train to cover 132 km is 1 hour less than the passenger train to cover the same distance. Therefore,
(132/x) – (132/(x+11)) = 1
132(x+11-x)/(x(x+11)) = 1
132 × 11 /(x(x+11)) = 1
⇒ 132 × 11 = x(x + 11)
⇒ x2 + 11x – 1452 = 0
⇒ x2 + 44x -33x -1452 = 0
⇒ x(x + 44) -33(x + 44) = 0
⇒ (x + 44)(x – 33) = 0
⇒ x = – 44, 33
As we know, speed cannot be negative.
Therefore, the speed of the passenger train will be 33 km/h and thus, the speed of the express train will be 33 + 11 = 44 km/h.
11. Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, find the sides of the two squares.
Solution:
Let the sides of the two squares be x m and y m.
Therefore, their perimeter will be 4x and 4y, respectively
And the area of the squares will be x2 and y2, respectively.
Given,
4x – 4y = 24
x – y = 6
x = y + 6
Also, x2 + y2 = 468
⇒ (6 + y2) + y2 = 468
⇒ 36 + y2 + 12y + y2 = 468
⇒ 2y2 + 12y + 432 = 0
⇒ y2 + 6y – 216 = 0
⇒ y2 + 18y – 12y – 216 = 0
⇒ y(y +18) -12(y + 18) = 0
⇒ (y + 18)(y – 12) = 0
⇒ y = -18, 12
As we know, the side of a square cannot be negative.
Hence, the sides of the squares are 12 m and (12 + 6) m = 18 m.
The NCERT Solutions Exercise 4.3 for Class 10 Maths Chapter 4 – Quadratic Equations contain solutions to a total of 11 questions. This is the third exercise of Chapter 4. The students can refer to the NCERT Solutions for reference, which contain detailed explanations of all the solutions. Conceptual knowledge of this chapter will help the students in solving several Maths problems in the higher classes.
Key Features of NCERT Solutions Class 10 Maths Chapter 4 – Quadratic Equations
- The solutions are by the subject experts.
- The answers are accurate.
- Each question is explained stepwise.
- The exercises provided in NCERT Class 10 Solutions will help the students score well in the examinations.
It is very helpful but changing word problem to equation is very hard