1. KCET
  2. KCET Question Papers
  3. KCET 2017 Physics Paper with Solutions

KCET 2017 Physics Paper with Solutions

KCET 2017 Paper with Solutions Physics is available here. Revise them and gain confidence, which in turn reduces the fear of facing the examination. It will help the students to attempt maximum questions in stipulated time by increasing their speed and accuracy. Candidates can download the previous years’ question papers of KCET to figure out the alternative and easy method to solve a particular problem. Practising the previous year papers is the best tool for the preparation of this competitive exam KCET, in terms of the syllabus and distribution of marks across different topics. Solving these papers with solutions will boost the candidates’ confidence and scores in the KCET examination.

KCET 2017 - Physics

Question 1: A substance of mass 49.53 g occupies 1.5 cm3 of volume. The density of the substance (in g cm3) with the correct number of significant figures is

  1. a. 3.302
  2. b. 3.300
  3. c. 3.3
  4. d. 3.30

Solution:

  1. Answer: (G)

    Bonus

Question 2: A car moving with a velocity of 20 ms–1 is stopped in a distance of 40 m. If the same car is travelling at double the velocity, the distance travelled by it for the same retardation is

  1. a. 640 m
  2. b. 320 m
  3. c. 1280 m
  4. d. 160 m

Solution:

  1. Answer: (d)

    Let the initial speed of car be u = 20 m / s

    Final speed of car; V = 0 m / s

    Retardation = a

    Case – I

    V2 = u2 + 2as

    0 = u2 + 2as

    – 400 / [2 * 40] = a

    [a = –5 m / s2]

    Case – II

    u = 40 m / s

    v = 0 m / s

    a = –5 m / s2

    s = ?

    V2 = u2 +2as

    0 = (40)2 + 2 (–5). S

    S = 1600 / 10

    S = 160 m

Question 3: The angle between velocity and acceleration of a particle describing uniform circular motion is

  1. a. 45º
  2. b. 60º
  3. c. 90º
  4. d. 180º

Solution:

  1. Answer: (c)

    In a circular motion, velocity is always tangential to the circular path. Also in a uniform circular motion, tangential acceleration is zero. Hence, the net acceleration will be centripetal acceleration which always acts towards the centre of the circular path. Hence, velocity and acceleration of a particle describing uniform circular motion are at a right angle to each other.

Question 4: If

\(\vec{A} = 2 \hat i + 3 \hat j + 8 \hat k\)
is perpendicular to
\(\vec{B} = 4 \hat j - 4 \hat i + \alpha \hat k\)
then the value of ‘α’ is

  1. a. 1 / 2
  2. b. -1 / 2
  3. c. 1
  4. d. –1

Solution:

  1. Answer: (b)

    When vectors are perpendicular to each other, then their dot product is zero.

    \(\vec{A} . \vec{B}\)
    = 0

    \((2 \hat i + 3 \hat j + 8 \hat k) . (4 \hat j - 4 \hat i + \alpha \hat k)\)
    = 0

    –8 + 12 + 8α = 0

    8α = - 4

    α = - 1 / 2

Question 5: A body of mass 50 kg, is suspended using a spring balance inside a lift at rest. If the lift starts falling freely, the reading of the spring balance is

  1. a. = 50 kg
  2. b. > 50 kg
  3. c. < 50 kg
  4. d. = 0

Solution:

  1. Answer: (d)

    As the lift is falling freely, therefore its acceleration = g (downwards)

    Let, the force acting on body due to spring is “F”

    ∴ (50g) – F = (50) a

    50g – F = 50 g

    F = 0

    Thus, no force is acting on the body due to spring.

    So, the reading of spring balance is zero.

Question 6: A motor pump lifts 6 tones of water from a well of depth 25m to the first floor of height 35 m from the ground floor in 20 minutes. The power of the pump (in kW) is [g = 10 ms–2]

  1. a. 3
  2. b. 6
  3. c. 1.5
  4. d. 12

Solution:

  1. Answer: (a)

    Power = work done / time taken

    P = mgh / t

    P = (m / t) gh

    h = 25 + 35 = 60m

    Flow rate = (m / t) = 6 tones / 20 min

    = {[6000] / [20 * 60]} (kg / sec) = 5 (kg / sec)

    P = 5 × 10 × 60

    = 3000 w

    = 3 kw

Question 7: Two balls are thrown simultaneously in the air. The acceleration of the centre of mass of the two balls when in air

  1. a. depends on the masses of the two balls
  2. b. depends on the speeds of the two balls
  3. c. is equal to g (Acceleration due to gravity)
  4. d. depends on the direction of motion of the two balls

Solution:

  1. Answer: (c)

    As there is no force in the horizontal direction, so there will be no acceleration of COM in a horizontal direction.

    As for vertical direction, the only gravitational force acts on both the balls, hence the acceleration of COM will be equal to the acceleration due to gravity which is ‘g’.

Question 8: The value of acceleration due to gravity at a depth of 1600 km is equal to [Radius of earth = 6400 km]

  1. a. 9.8 ms–2
  2. b. 19.6 ms–2
  3. c. 4.9 ms–2
  4. d. 7.35 ms–2

Solution:

  1. Answer: (d)

    Acceleration due to gravity at a depth “d”:

    gd = g (1 - [d / Re])

    d → 1600km

    Re → 6400 km

    g → 9.8 m / s2

    gd = (9.8) (1 - [1600 / 6400])

    gd = 7.35 ms–2

Question 9: ‘Young’s modulus is defined as the ratio of

  1. a. tensile stress and longitudinal strain
  2. b. hydraulic stress and hydraulic strain
  3. c. shearing stress and shearing strain
  4. d. bulk stress and longitudinal strain

Solution:

  1. Answer: (a)

    Young’s modulus is defined as the ratio of tensile stress to tensile strain or longitudinal strain.

Question 10: ‘Hydraulic lift’ works on the basis of

  1. a. Stoke’s law
  2. b. Toricelli’s law
  3. c. Pascal’s law
  4. d. Bernoulli’s law

Solution:

  1. Answer: (c)

    Hydraulic lift works on the principle of equal transmission throughout a fluid i.e. pascal’s law.

Question 11: The S.I. unit of specific heat capacity is

  1. a. J mol–1 K–1
  2. b. J kg–1 K–1
  3. c. J K–1
  4. d. J kg

Solution:

  1. Answer: (b)

    Specific heat capacity: S = (Q / mΔT)

    Q → Amount of heat absorbed

    M → Mass of the substance

    T → Change in temperature of the substance

    SI unit of S → J kg–1 K–1

Question 12: For which combination of working temperatures, the efficiency of ‘Carnot’s engine’ is the least?

  1. a. 60K, 40 K
  2. b. 40K, 20K
  3. c. 80K, 60K
  4. d. 100K, 80K

Solution:

  1. Answer: (d)

    The efficiency of Carnot’s engine; 𝜂 = 1 - [Tlower / Thigher]

    Now, let’s check options.

    (A) → 𝜂A = 1 - (40 / 60) = 0.33

    (B) → 𝜂B = 1 - (20 / 40) = 0.5

    (C) → 𝜂C = 1 - (60 / 80) = 0.25

    (D) → 𝜂D = 1 - (80 / 100) = 0.2

Question 13: The mean energy of a molecule of an ideal gas is

  1. a. 2 KT
  2. b. [3 / 2] KT
  3. c. KT
  4. d. 1 / 2 KT

Solution:

  1. Answer: (b)

    Mean energy of a molecule of an ideal gas:

    E = (1 / 2) mV2rms

    Rms velocity of molecules: Vrms = √3KT / m

    E = (1 / 2) × m × (3KT / m)

    E = (3 / 2) KT

Question 14: Two simple pendulums A and B are made to oscillate simultaneously and it is found that A completes 10 oscillations in 20 sec and B completes 8 oscillations in 10 sec. The ratio of the lengths of A and B is

  1. a. 8 / 5
  2. b. 64 / 25
  3. c. 5 / 4
  4. d. 25 / 64

Solution:

  1. Answer: (b)

    The time period of the simple pendulum: T = 2π √(l / g)

    lA / lB = [TA / TB]2

    Time period of A: TA = 20 / 10 = 2 sec

    Time period of B: TB = 10 / 8 = 5 / 4 sec

    lA / lB = 64 / 25

Question 15: The waves set up in a closed pipe are

  1. a. Transverse and progressive
  2. b. Longitudinal and stationary
  3. c. Transverse and stationary
  4. d. Longitudinal and progressive

Solution:

  1. Answer: (b)

    The waves set up in a closed pipe are longitudinal and stationary because of the superposition of incident wave and reflected wave.

Question 16: Two spheres of electric charges +2 nC and −8 nC are placed at a distance‘d’ apart. If they are allowed to touch each other, what is the new distance between them to get a repulsive force of the same magnitude as before?

  1. a. 4d / 3
  2. b. 3d / 4
  3. c. d
  4. d. d / 2

Solution:

  1. Answer: (b)

    Case – I:

    KCET 2017 Physics Paper With Solutions Q16

    F = KqAqB / r2

    F = [K . 2 . 8] / d2

    F = 16K / d2

    Case – II:

    KCET 2017 Physics Paper Q16

    qA = qB = (2 - 8) / 2 = -6 / 2 = -3 nc

    KCET 2017 Physics Paper With Solutions Question number 16

    F’ = K (3) (3) / d2

    But F = 16k / d2

    16k / d2 = 9k / r2

    r2 = (9 / 16) d2

    r = (3 / 4) d

Question 17: Three-point charges of +2q, + 2q and –4q are placed at the corner A, B and C of an equilateral triangle ABC of side ‘x’. The magnitude of the electric dipole moment of this system is

  1. a. 2 qx
  2. b. 2 √3 qx
  3. c. 3 √2 qx
  4. d. 3 qx

Solution:

  1. Answer: (b)

    KCET 2017 Physics Paper With Solutions Q17

    As evident from the diagram above, we can consider two dipoles one CA and CB. M1: Dipole moment of CA = 2q x (from C to A)

    M2: Dipole moment of CB = 2qx (from C to B)

    KCET 2017 Physics Paper Q17

    Net dipole moment = √[m12 + m22 + 2m1 m2 cos 60º]

    = √[m12 + m22 + 2m1 m2 (1 / 2)]

    = √[m12 + m22 + 2m1 m2]

    = √(4q2x2 + 4q2x2 + 4q2x2)

    = 2 √3 qx

Question 18: 4 × 1010 electrons are removed from a neutral metal sphere of diameter 20 cm placed in air. The magnitude of the electric field (in NC–1) at a distance of 20 cm from its centre is

  1. a. 5760
  2. b. 1440
  3. c. 640
  4. d. Zero

Solution:

  1. Answer: (b)

    Total charge removed from sphere = ne

    = (4 × 1010) × (1.6 × 10–19)

    = 6.4 × 10–9 C

    Distance of point from centre of sphere = 20 cm = 0.2 m

    Electric field: E = kq / r2

    E = [9 × 109 × (6.4 × 10-9)] / (0.2)2

    = 1440 N / C

Question 19: Two-point charges A = +3 nC and B = 1nC are placed 5 cm apart in the air. The work done to move charge B towards A by 1 cm is

  1. a. 1.35 × 10–7 J
  2. b. 2.7 × 10–7 J
  3. c. 2.0 × 10–7 J
  4. d. 12.1 × 10–7 J

Solution:

  1. Answer: (a)

    Potential energy of system: u = [KQAQB] / d

    Initial distance between charges → 5 cm = 0.05m

    Uinitial = [(9 × 109) × (3 × 10-9) × (1 × 10-9)] / 0.05

    = 5.4 × 10–7 J

    Ufinal = [(9 × 109) × (3 × 10-9) × (1 × 10-9)] / 0.04

    = 6.75 × 10–7 J

    Work done: W = uf – ui

    W = (6.75 – 5.4) × 107

    = 1.35 × 107 J

Question 20: A system of 2 capacitors of capacitance 2μF and 4μF is connected in series across a potential difference of 6V. The electric charge and energy stored in the system are

  1. a. 10 μC and 30 μJ
  2. b. 36 μC and 108 μJ
  3. c. 8 μC and 24 μJ
  4. d. 1 μC and 2 μJ

Solution:

  1. Answer: (c)

    Equivalent capacitance: Ceq = [C1C2] / [C1 + C2] = [2 × 4] / [2 + 4]

    KCET 2017 Physics Paper With Solutions Q20

    Ceq = 4μF / 3

    Charge: q = cv

    Q = (4 / 3) * 6 = 8μC

    Energy stored: E = (1 / 2) CV2 = (1 / 2) (4 / 3) 62 = 24 μJ

Question 21: The minimum value of effective capacitance that can be obtained by combining 3 capacitors of capacitances 1pF, 2pF and 4pF is

  1. a. (4 / 7) pF
  2. b. 1 pF
  3. c. (7 / 4) pF
  4. d. 2 pF

Solution:

  1. Answer: (a)

    Minimum capacitance can be obtained by connecting these three capacitors in series.

    (1 / Ceq) = (1 / C1) + (1 / C2) + (1 / C3)

    = (1 / 1) + (1 / 2) + (1 / 4)

    = [7 / 4]

    Ceq = (4 / 7) pF

Question 22: A cylindrical conductor of diameter 0.1 mm carries a current of 90 mA. The current density (in Am–2) is (π ≃ 3)

  1. a. 1.2 × 107
  2. b. 2.4 × 107
  3. c. 3 × 106
  4. d. 6 × 106

Solution:

  1. Answer: (a)

    Current density: J = I / A

    Current: I → 90 mA = 90 × 10–3 A

    Diameter of wire: d = 0.1mm = 10–4 m2

    The cross-section area of wire; A = πd2 / 4

    A = [3 × (10-4)2] / 4 = 0.75 × 10–8 m2

    J = [90 × 10-3] / [0.75 × 10-8] = 1.2 × 107 A / m2

Question 23: A piece of copper is to be shaped into a conducting wire of maximum resistance. The suitable length and diameter are _________ and ____________respectively.

  1. a. L and d
  2. b. 2 L and d
  3. c. L / 2 and 2 d
  4. d. L and d / 2

Solution:

  1. Answer: (d)

    Resistance of copper wire: R = ρL / A

    ρ → Resistivity of material and is constant

    L → Length of wire

    A → Cross-sectional area of conductor

    A = πd2 / 4

    D → diameter of the wire

    R ∝ L / d2

    Now, let’s check the options

    (A) RA ∝ (L / d2)

    (B) RB ∝ 2 (L / d2)

    (C) RB ∝ (1 / 8) (L / d2)

    (D) RD ∝ 8 (L / d2)

Question 24: Of the following graphs, the one that correctly represents the I –V characteristics of a ‘Ohmic device’ is

KCET 2017 Physics Paper With Solutions Q24

    Solution:

    1. Answer: (c)

      Ohmic device, obey ohm’s law, i.e. V = IR

      V ∝ I (R → constant)

      I – V characteristic will be a straight line

      KCET 2017 Physics Paper Q24

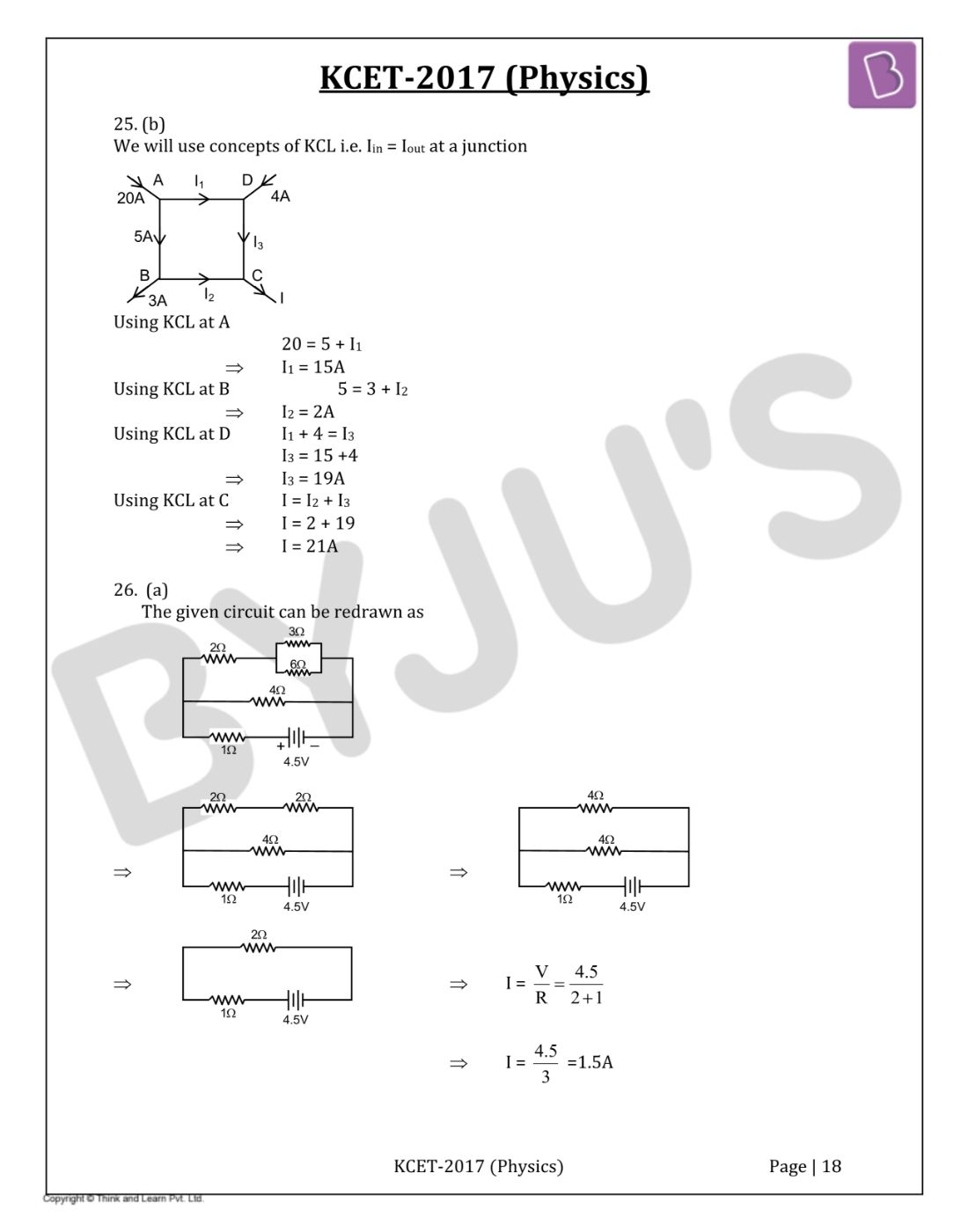
    Question 25: The value of I in the figure shown below is

    KCET 2017 Physics Paper With Solutions Q25

    1. a. 8A
    2. b. 21A
    3. c. 19A
    4. d. 4A

    Solution:

    1. Answer: (b)

      We will use concepts of KCL i.e. Iin = Iout at a junction.

      KCET 2017 Physics Paper Q25

      Using KCL at A

      20 = 5 + I1

      I1 = 15A

      Using KCL at B

      5 = 3 + I2

      I2 = 2A

      Using KCL at D

      I1 + 4 = I3

      I3 = 15 + 4

      I3 = 19A

      Using KCL at C

      I = I2 + I3

      I = 2 + 19

      I = 21A

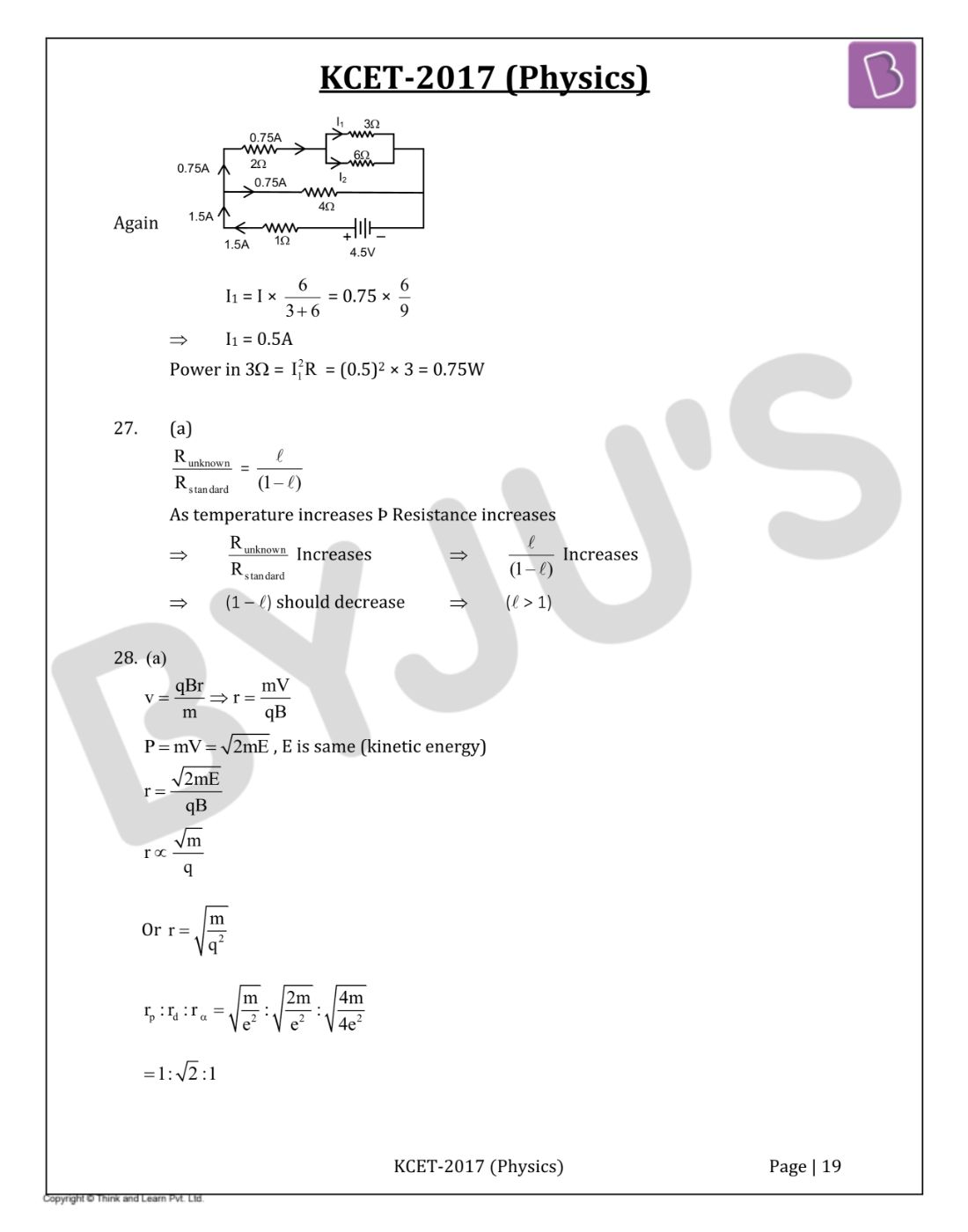
    Question 26: The power dissipated in 3Ω resistance in the following circuit is

    KCET Solved 2017 Physics Paper

    1. a. – 261 kJ
    2. b. + 103 kJ
    3. c. +261 kJ
    4. d. –103 kJ

    Solution:

    1. Answer: (a)

      The given circuit can be redrawn as

      KCET 2017 Physics Paper Q26

      Again
      KCET 2017 Physics Paper With Solutions Questions 26

      I1 = I × (6 / [3 + 6]) = 0.75 × (6 / 9)

      I1 = 0.5A

      Power in 3Ω = I12R = (0.5)2 3 = 0.75W

    Question 27: In metre bridge experiment, with a standard resistance in the right gap and a resistance coil dipped in water (in a beaker) in the left gap, the balancing length obtained is ‘I’. If the temperature of the water is increased, the new balancing length is

    1. a. > 1
    2. b. < 1
    3. c. = 1
    4. d. = 0

    Solution:

    1. Answer: (a)

      Runknown / Rstandard = l / (1 - l)

      As temperature increases Þ Resistance increases

      Runknown / Rstandard increases ⇒ l / (1 - l) increases

      (1 – l) should decrease ⇒ (l > 1)

    Question 28: A proton, a deuteron and an α - particle is projected perpendicular to the direction of a uniform magnetic field with same kinetic energy. The ratio of the radii of the circular paths described by them is

    1. a. 1 : √2 : 1
    2. b. 1 : √2 : √2
    3. c. √2 : 1 : 1
    4. d. √2 : √2 : 1

    Solution:

    1. Answer: (a)

      v = qBr / m ⇒ r = mV / qB

      P = mV = √2mE, E is same (kinetic energy)

      r = √2mE / qB

      r ∝ √m / q

      r = √m / q2

      rp . rd . rα = √(m / e2) : √(2m / e2) : √(4m / e2)

      = 1 : √2 : 1

    Question 29: A galvanometer of resistance 50 Ω is connected to a battery of 3V along with a resistance of 2950 Ω in series shows full-scale deflection of 30 divisions. The additional series resistance required to reduce the deflection to 20 divisions is

    1. a. 1500 Ω
    2. b. 4440 Ω
    3. c. 7400 Ω
    4. d. 2950 Ω

    Solution:

    1. Answer: (b)

      Total internal resistance = G + R

      = 50 + 2950 = 3000Ω

      Current; I = 3 / 3000 = 10–3A = 1 mA

      If the deflection is to be reduced to 20 divisions

      I’ = [1 mA / 30] * 20 = (2 / 3) mA

      Let x be the effective resistance of the circuit.

      3V = 3000 Ω × 1mA = x Ω * (2 / 3) mA

      x = 4500 Ω

      Resistance to be added = (4500 – 50) Ω

      = 4450 Ω

      ≈ 4440 Ω

    Question 30: The magnetic field at the centre of a current-carrying loop of radius 0.1 m is 5 √5 times that at a point along its axis. The distance of this point from the centre of the loop is

    1. a. 0.2 m
    2. b. 0.1m
    3. c. 0.05m
    4. d. 0.25m

    Solution:

    1. Answer: (a)

      For a circular current-carrying loop of radius R

      Bcentre = μ0i / 2R

      Baxis = μ0iR2 / 2 [R2 + x2]3/2 [at a distance x from the centre]

      Given Bcentre = 5 √5 Baxis

      [μ0i / 2R] = [5 √5] [μ0iR2 / 2 [R2 + x2]3/2]

      [R2 + x2]3 / R6 = 125

      [R2 + x2] / R2 = 5

      x2 / R2 = 4

      x = 2R

      x = 2 × 10 = 20 cm = 0.2m

    Question 31: A straight wire of length 50 cm carrying a current of 2.5 A is suspended in mid-air by a uniform magnetic field of 0.5 T (as shown in the figure). The mass of the wire is (g = 10 ms–2)

    KCET 2017 Physics Paper With Solutions Q31

    1. a. 62.5 gm
    2. b. 250 gm
    3. c. 125 gm
    4. d. Cu2O + FeS

    Solution:

    1. Answer: (a)

      For equilibrium

      FB = mg

      Bil = mg

      m = Bil / g

      m = [0.5 × 2.5 × 50 × 10-2] / 10 = 62.5 g

    Question 32: Which of the following properties is ‘False’ for a bar magnet?

    1. a. Its poles cannot be separated.
    2. b. It points in North-South direction when suspended
    3. c. It’s like poles repel and unlike poles attract.
    4. d. It doesn’t produce a magnetic field

    Solution:

    1. Answer: (d)

      A bar magnet can produce a magnetic field. Option (d) is False.

    Question 33: A magnetic dipole of the magnetic moment 6 × 10–2 Am2 and moment of inertia 12 × 10–6 kgm2 performs oscillation in a magnetic field of 2 × 10–2 T. The time taken by the dipole to complete 20 oscillations is (π ≃ 3)

    1. a. 36 s
    2. b. 6s
    3. c. 12 s
    4. d. 18 s

    Solution:

    1. Answer: (c)

      Time period of oscillation

      T = 2π √I / MB

      = 2π √[12 × 10-6] / [(6 × 10-2) (2 × 10-2)]

      = 2π √(12 × 10-6) / (12 × 10-4)

      = 2π × 10-1

      For 20 oscillations,

      T’ = 20 × 2π × 10–1

      T’ = 12 sec

    Question 34: The susceptibility of a ferromagnetic substance

    1. a. >>1
    2. b. > 1
    3. c. < 1
    4. d. zero

    Solution:

    1. Answer: (a)

      Susceptibility of Ferromagnetic substance is >>>1 because it is strongly attracted to an external magnetic field.

    Question 35: A bar magnet is allowed to fall vertically through a copper coil placed in a horizontal plane. The magnet falls with a net acceleration

    KCET 2017 Physics Paper With Solutions Q35

    1. a. = g
    2. b. > g
    3. c. < g
    4. d. zero

    Solution:

    1. Answer: (c)

      If the magnet is falling vertically down with its north pole towards the coil, then the upper face of the coil will become north pole, So that it can oppose the approaching north pole of the magnet. Here, the acceleration will be less than “g”.

    Question 36: The working of magnetic braking of trains is based on

    1. a. Alternating current
    2. b. Eddy current
    3. c. Steady current
    4. d. Pulsating current

    Solution:

    1. Answer: (b)

      Working of magnetic breaking in the train is based on eddy current.

    Question 37: A jet plane of wingspan 20 m is travelling towards the west at a speed of 400 ms–1. If the earth’s total magnetic field is 4× 10–4 T and the dip angle is 30º, at that place, the voltage difference developed across the ends of the wing is

    1. a. 1.6 V
    2. b. 3.2 V
    3. c. 0.8 V
    4. d. 6.4 V

    Solution:

    1. Answer: (a)

      Voltage difference = BlV sin θ

      = (4 × 10–4) × (20) × (400) sin 30º

      = 1.6 V

    Question 38: In the A.C. circuit shown, keeping ‘K’ pressed if an iron rod is inserted into the coil, the bulb in the circuit,

    KCET 2017 Physics Paper With Solutions Q38

    1. a. Glows more brightly
    2. b. Glows less brightly
    3. c. Glows with same brightness (as before the rod is inserted)
    4. d. Gets damaged

    Solution:

    1. Answer: (b)

      When the iron rod is inserted in the coil, then the inductive increases, hence the current flowing through the bulb decreases, therefore brightness decreases.

    Question 39: The output of a step-down transformer is measured to be 48 V when connected to a 12 w bulb. The value of peak current is

    1. a. (1 / √2) A
    2. b. (√2) A
    3. c. (1 / 2√2) A
    4. d. (1 / 4) A

    Solution:

    1. Answer: (c)

      P = V.I.

      I = P / V

      I = 12 / 48 = 0.25 A

      Peak current = √2 I

      = √2 * (1 / 4)

      = (1 / 2√2) A

    Question 40: A coil of inductive reactance (1 / √3) Ω and resistance 1Ω is connected to a 200 V, 50 Hz A.C. supply. The time lag between the maximum voltage and current is

    1. a. (1 / 300) s
    2. b. (1 / 600) s
    3. c. (1 / 500) s
    4. d. (1 / 200) s

    Solution:

    1. Answer: (b)

      ω = 2πf

      ω = 2 * 3.14 * 50

      tan ϕ = xL / R = ωL / R = (1 / √3) / 1 = 1 / √3

      ϕ = 30o

      ωt = π / 6

      t = π / [6 * ω]

      t = [3.14] / [6 * 314]

      t = (1 / 600) sec

    Question 41: If E and B represent electric and magnetic field vectors of an electromagnetic wave, the direction of propagation of the wave is along

    1. a. E
    2. b. B
    3. c. E × B
    4. d. B × E

    Solution:

    1. Answer: (c)

      As we know, by property of the electromagnetic wave, the electric field, magnetic field & the direction of propagation, all the three are mutually perpendicular. Thereby right-hand thumb rule using the figure. E × B.

      KCET 2017 Physics Paper With Solutions Q41

    Question 42: According to Cartesian sign convention, in ray optics

    1. a. all distances are taken positive
    2. b. all distances are taken negative
    3. c. all distances in the direction of the incident ray are taken positive
    4. d. all distances in the direction of the incident ray are taken negative

    Solution:

    1. Answer: (c)

      In ray optics, all the directions in the direction of the incident ray are taken as positive.

    Question 43: A linear object of height 10 cm is kept in front of a concave mirror of radius of curvature 15 cm, at a distance of 10 cm. The image formed is

    1. a. magnified
    2. b. magnified and inverted
    3. c. diminished and erect
    4. d. diminished and inverted

    Solution:

    1. Answer: (b)

      Using mirror formula

      (1 / f) = (1 / u) + (1 / v)

      f = R / 2 = 15 / 2

      (1 / [-15 / 2]) = (1 / -10) + (1 / v)

      V = –30 cm

      Magnification, m = −v/u = −30 / −10 = −3

      Therefore, The image formed is real, magnified and inverted.

    Question 44: During scattering of light, the amount of scattering is inversely proportional to _______ of the wavelength of light,

    1. a. cube
    2. b. square
    3. c. fourth power
    4. d. Half

    Solution:

    1. Answer: (c)

      During scattering of light

      Intensity: I ∝ (1 / λ4)

    Question 45: In Young’s double-slit experiment if yellow light is replaced by blue light, the interference fringes become

    1. a. wider
    2. b. narrower
    3. c. brighter
    4. d. darker

    Solution:

    1. Answer: (b)

      Fringe width: w = Dλ / d

      w ∝ λ

      But λyellow light > λblue light

      Interference patterns will become narrower.

    Question 46: According to Huygens’ principle, during refraction of light from air to a denser medium

    1. a. Wavelength and speed decrease
    2. b. Wavelength and speed increase
    3. c. Wavelength increases but speed decreases
    4. d. Wavelength decreases but speed increases

    Solution:

    1. Answer: (a)

      Refractive index of the medium

      μ = c / v

      C → speed of light in vacuum or air

      V → speed of light in the medium

      Above equation implies that the speed of light decrease when it goes from rarer medium (air) to denser medium

      Also; λ = v / f

      λ = wavelength, f → frequency

      Frequency remains the same for all medium unless the source of light is disturbed

      λ ∝ V

      Wavelength decreases.

    Question 47: In a system of two crossed polarizers, it is found that the intensity of light from the second polarizer is half from that of the first polariser. The angle between their pass axes is

    1. a. 45º
    2. b. 60º
    3. c. 30º
    4. d. 0º

    Solution:

    1. Answer: (a)

      From Malus law

      I = I0 cos2 θ

      There; I = I0 / 2

      I0 / 2 = I0 cos2 θ

      cos θ = 1 / √2

      θ = 45o

    Question 48: From the following graph of photocurrent against collector plate potential, for two different intensities of light I1 and I2, one can conclude

    KCET 2017 Physics Paper With Solutions Q48

    1. a. I1 = I2
    2. b. I1 > I2
    3. c. I1 < I2
    4. d. Comparison is not possible

    Solution:

    1. Answer: (c)

      The value of photocurrent depends on the intensity of incident light. So, when the intensity of incident light increases, then the value of photocurrent is increased. The intensity of light ∝ photocurrent.

      KCET 2017 Physics Paper Solved Papers

      I1 < I2

    Question 49: A particle is dropped from a height ‘H’. The de’Broglie wavelength of the particle depends on height as

    1. a. H
    2. b. H0
    3. c. H1/2
    4. d. H–1/2

    Solution:

    1. Answer: (d)

      From de-broglie expression

      λ = h / mv

      λ = h / [m √2gH]

      λ ∝ H–1/2

    Question 50: The scientist who is credited with the discovery of ‘nucleus’ in an atom is

    1. a. J.J. Thomson
    2. b. Rutherford
    3. c. Niels Bohr
    4. d. Balmer

    Solution:

    1. Answer: (b)

      Rutherford is credited with the discovery of nucleus in an atom.

    Question 51: The energy (in eV) required to excite an electron from n = 2 to n = 4 state in the hydrogen atom is

    1. a. + 2.55
    2. b. – 3.4
    3. c. – 0.85
    4. d. + 4.25

    Solution:

    1. Answer: (a)

      The expression of energy is En = 13.6 / n2

      The required energy is E = E2 - E4 = (13.6 / 22) - (13.6 / 42)

      = +2.55

    Question 52: In a nuclear reactor the function of the Moderator is to decrease

    1. a. Number of neutrons
    2. b. Speed neutrons
    3. c. Escape of neutrons
    4. d. Temperature of the reactor

    Solution:

    1. Answer: (b)

      In a nuclear reactor, the function of the moderator is to decrease the speed of neutrons.

    Question 53: The particles emitted in the decay of 23892U to 23492U

    1. a. 1 α and 2 β
    2. b. 1 α only
    3. c. 1 α and 1 β
    4. d. 2 α and 2 β

    Solution:

    1. Answer: (a)

      KCET 2017 Physics Paper With Solutions Q53

      ∴ 1 α and 2 β particles

    Question 54: The mass defect of 42He is 0.03μ. The binding energy per nucleon of helium (in MeV) is

    1. a. 27.93
    2. b. 6.9825
    3. c. 2.793
    4. d. 69.825

    Solution:

    1. Answer: (b)

      The mass defect of 42He; ΔM = 0.03u

      Binding energy of helium: E = ΔM × 931 MeV

      E = 0.03 × 931.5 = 27.93 MeV

      Number of nucleons in helium; n = 4

      Binding energy per nucleon = E / n = 27.93 / 4 = 6.9825

    Question 55: The energy gap in case of which of the following is less than 3 eV?

    1. a. copper
    2. b. Iron
    3. c. Zener diode
    4. d. Germanium

    Solution:

    1. Answer: (d)

      In Germanium energy the gap is less than 3eV.

    Question 56: Which of the following semiconducting devices is used as a voltage regulator?

    1. a. Photo diode
    2. b. LASER diode
    3. c. Zener diode
    4. d. Solar cell

    Solution:

    1. Answer: (c)

      Zener diode is used as a voltage regulated as in reverse biased condition it exhibits constant voltage.

    Question 57: In the three parts of a transistor, ‘Emitter is of

    1. a. Moderate size and heavily doped
    2. b. Large size and lightly doped
    3. c. Thin size and heavily doped
    4. d. Large size and moderately doped

    Solution:

    1. Answer: (a)

      In the case of a transistor, the emitter is of moderate size and heavily doped so as to supply a large number of majority charge carriers for current flow.

    Question 58: In the figure shown, if the diode forward voltage drop is 0.2 V, the voltage difference between A and B is

    KCET 2017 Physics Paper With Solutions Q58

    1. a. 1.3 V
    2. b. 2.2 V
    3. c. 0
    4. d. 0.5 V

    Solution:

    1. Answer: (b)

      The voltage drop across AB by using KVL is as follows:

      VAB = (0.2 × 10-3 × 5 × 103) + 0.2 + (0.2 × 10-3 × 5 × 103)

      = 1 + 0.2 + 1

      = 2.2V

    Question 59: Which of the following logic gates is considered as ‘universal’?

    KCET 2017 Physics Paper With Solutions Q59

      Solution:

      1. Answer: (d)

        NAND and NOR gates are considered as universal gates. Out of the given options, an option (D) is NAND gate.

      Question 60: A basic communication system consists of

      (a) Transmitter

      (b) Information source

      (c) User of information

      (d) Channel

      (e) Receive

      1. a. a, b, c, d and e
      2. b. b, a, d, e and c
      3. c. b, d, a, c and e
      4. d. b, e, a, d and c

      Solution:

      1. Answer: (b)

        The block diagram of the communication system is as follows:

        KCET 2017 Physics Paper With Solutions Q60

      Video Lessons - KCET 2017 - Physics









      KCET 2017 Physics Question Paper with Solutions

      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions
      KCET 2017 Physics Question Paper with Solutions