1. KCET
  2. KCET Question Papers
  3. KCET 2018 Maths Paper with Solutions

KCET 2018 Maths Paper with Solutions

KCET 2018 paper with solutions Maths is a perfect resource for those who are preparing for KCET examination. The first step towards the KCET Exam Preparation is to solve KCET Previous Year Question Papers. Along with the question paper, the answer key of KCET 2018 has also been provided here. Solving KCET previous year papers will give you an idea about the nature and pattern of questions asked in the exam. It will help the students to get a clear idea about the amount of preparation required to face the exam.

KCET 2018 - Maths

Question 1: If |x + 5| ≥ 10 then

  1. a. x ∈ (–15, 5]
  2. b. x ∈ (–5, 5]
  3. c. x ∈ (–∞, –15] ∪ [5, ∞)
  4. d. x ∈ [–∞, –15] ∪ [5, ∞)

Solution:

  1. Answer: (c)

    ⇒ |x + 5| ≥ 10

    ⇒ x + 5 ≤ –10 or x + 5 ≥ 10

    ⇒ x ≤ –15 or x ≥ 5

    ⇒ x ∈ (–∞, –15] ∪ [5, ∞)

Question 2: Everybody in a room shakes hands with everybody else. The total number of handshakes is 45. The total number of persons in the room is

  1. a. 9
  2. b. 10
  3. c. 5
  4. d. 15

Solution:

  1. Answer: (b)

    Let the total number of handshake = nC2

    We know ⇒ nC2 = 45

    ⇒ n! / 2! !(n - 2)! = 45

    ⇒ n (n - 1) / 2 = 45

    ⇒ n2 – n – 90 = 0

    ⇒ n = 10, –9 (not possible)

    Total no. of persons in the room is 10.

Question 3: The constant term in the expansion of (x2 - [1 / x2])16 is

  1. a. 16C8
  2. b. 16C7
  3. c. 16C9
  4. d. 16C10

Solution:

  1. Answer: (a)

    Let Tr+1 be the constant term.

    ⇒ Tr+1 = 16Cr (x2)16-r (1 / x2)r

    = 16Cr x32 - 4r

    For constant term 32 – 4r = 0

    ⇒ 4r = 32

    ⇒ r = 8

    ⇒ T8+1 = 16C8

Question 4: If P (n): “22n –1 is divisible by k for all n ∈ N” is true, then the value of ‘k’ is

  1. a. 6
  2. b. 3
  3. c. 7
  4. d. 2

Solution:

  1. Answer: (b)

    P(1) = 22×1 –1 = 4 – 1 = 3

    P(2) = 22×2 –1 = 16 – 1 = 15

    We can say 3 is the only prime number which is divisible by 3 and 15.

    So the value of K = 3

Question 5: The equation of the line parallel to the line 3x – 4y + 2 = 0 and passing through (–2, 3) is

  1. a. 3x – 4y + 18 = 0
  2. b. 3x – 4y – 18 = 0
  3. c. 3x + 4y + 18 = 0
  4. d. 3x + 4y – 18 = 0

Solution:

  1. Answer: (a)

    Let line which is parallel to given line is –

    ⇒ 3x – 4y + λ = 0 … (1)

    This line is passing through (–2, 3)

    ⇒ 3 (–2) – 4 (3) + λ = 0

    ⇒ λ = 18 {put in equation (1)}

    ⇒ Equation of line = 3x – 4y + 18 = 0

Question 6: If ([1 - i] / [1 + i])96 = a + ib then (a, b) is

  1. a. (1, 1)
  2. b. (1, 0)
  3. c. (0, 1)
  4. d. (0, –1)

Solution:

  1. Answer: (b)

    ⇒ ([1 - i] / [1 + i])96

    \(\Rightarrow [\frac{(1-i)(1-i)}{(1+i)(1-i)}]^{96}\\ \Rightarrow [\frac{-2i}{2}]^{96}\\ \Rightarrow [-i]^{96}= 1+0i = a+ib\\\)

    On comparing both sides

    (a, b) = (1, 0)

Question 7: The distance between the foci of a hyperbola is 16 and its eccentricity is √2. Its equation is

  1. a. x2 – y2 = 32
  2. b. [x2 / 4] - [y2 / 9] = 1
  3. c. 2x2 – 3y2 = 7
  4. d. y2 – x2 = 32

Solution:

  1. Answer: (a, d)

    Distance between the foci of the hyperbola

    ⇒ 2ae = 16 {e = √2 given}

    ⇒ a = 4√2

    ⇒ e2 = 1 + (b2 / a2)

    ⇒ b2 = a2 (e2 - 1)

    ⇒ b2 = 32 (2 - 1) = 32

    ⇒ b = 4√2

    Equation of hyperbola is [x2 / a2] - [y2 / b2] = 1

    ⇒ [x2 / 32] - [y2 / 32] = 1

    ⇒ x2 - y2 = 32

    ⇒ Equation of conjugate hyperbola is x2 – y2 = –32

    Because eccentricity of C.H. is √2.

Question 8: The number of ways in which 5 girls and 3 boys can be seated in a row so that no two boys are together is

  1. a. 14040
  2. b. 14440
  3. c. 14000
  4. d. 14400

Solution:

  1. Answer: (d)

    No two are together = 5! × 6C3 × 3! (gap method)

    = 120 × 20 × 6

    = 14400

Question 9: If a, b, c are three consecutive terms of an AP and x, y, z are three consecutive terms of a GP, then the value of xb–c . yc–a . za–b is

  1. a. 0
  2. b. xyz
  3. c. -1
  4. d. 1

Solution:

  1. Answer: (d)

    2b = a + c …(1)

    y2 = xz …(2)

    = xb–c . yc–a . za–b

    = xa-b . x(c-a)/2 . z(c-a)/2 . za–b

    = x(a-2b+c)/2 . z(a-2b+c)/2

    = x0 . z0 = 1

Question 10: The value of limx→0 |x| / x is

  1. a. 1
  2. b. -1
  3. c. 0
  4. d. Does not exist

Solution:

  1. Answer: (d)

    LHL: limx→0- [-x / x] = -1

    RHL: limx→0+ [x / x] = 1

    ⇒ LHL ≠ RHL

    ⇒ The limit does not exist.

Question 11: Let f (x) = x – (1 / x) then f’(–1) is

  1. a. 0
  2. b. 2
  3. c. 1
  4. d. -2

Solution:

  1. Answer: (b)

    f (x) = x – (1 / x)

    On differentiating

    f ‘ (x) = 1 + (1 / x2)

    f’ (-1) = 1 + (1 / 1) = 2

Question 12: The negation of the statement “72 is divisible by 2 and 3” is

  1. a. 72 is not divisible by 2 or 72 is not divisible by 3
  2. b. 72 is divisible by 2 or 72 is divisible by 3
  3. c. 72 is divisible by 2 and 72 is divisible by 3
  4. d. 72 is not divisible by 2 and 3

Solution:

  1. Answer: (a)

    p : 72 is divisible by 2

    q : 72 is divisible by 3

    p: 72 is not divisible by 2

    q : 72 is not divisible by 3

    ⇒ (p ∧ q) = p ∨ q

    ⇒ 72 is not divisible by 2 or 72 is not divisible by 3.

Question 13: The probability of happening of an event A is 0.5 and that of B is 0.3. If A and B are mutually exclusive events, then the probability of neither A nor B is

  1. a. 0.4
  2. b. 0.5
  3. c. 0.2
  4. d. 0.9

Solution:

  1. Answer: (c)

    P (A) = 0.5

    P (B) = 0.3

    P (A ∩ B) = 0

    P (A ∪ B) = P (A) + P (B) – P (A ∩ B)

    = 0.5 + 0.3 – 0 = 0.8

    ⇒ P (A ∪ B)' = 1 – P (A ∪ B)

    = 1 - 0.8 = 0.2

Question 14: In a simultaneous throw of a pair of dice, the probability of getting a total of more than 7 is

  1. a. 7 / 12
  2. b. 5 / 36
  3. c. 5 / 12
  4. d. 7 / 36

Solution:

  1. Answer: (c)

    No. of ways of getting total more than 7 = {(6, 6), (6, 5), (5, 6), (6, 4), (4, 6), (6, 3), (3, 6), (6, 2), (2, 6), (5, 5), (5, 4), (4, 5), (5, 3), (3, 5), (4, 4)}= 15

    Probability of getting total more than 7 is = 15 / 36 = 5 / 12

Question 15: If A and B are mutually exclusive events given that P (A) = 3 / 5, P (B) = 1 / 5, then P (A or B) is

  1. a. 0.8
  2. b. 0.6
  3. c. 0.4
  4. d. 0.2

Solution:

  1. Answer: (a)

    P (A) = 3 / 5

    P (B) = 1 / 5

    P (A ∩ B) = 0

    P (A ∪ B) = P (A) + P (B) – P (A ∩ B)

    = (3 / 5) + (1 / 5) + 0

    = 4 / 5 = 0.8

Question 16: Let f, g : R → R be two functions define as f (x) = |x| + x and g (x) = |x| – x ∀ x ∈ R. Then (fog) (x) for x < 0 is

  1. a. 0
  2. b. 4x
  3. c. -4x
  4. d. 2x

Solution:

  1. Answer: (c)

    f (x) = |x| + x

    g (x) = |x| – x

    f [g (x)] = f [|x| – x]

    = ||x| - x| + |x| - x [x < 0]

    = |-2x| + (-2x)

    = –2x –2x

    = –4x

Question 17: A is a set having 6 distinct elements. The number of distinct functions from A to A which are not bijections is

  1. a. 6! – 6
  2. b. 66 – 6
  3. c. 66 – 6!
  4. d. 6!

Solution:

  1. Answer: (c)

    Total no. of functions from A → A is = 66

    Total no. of bijective functions = 6!

    No. of not bijective functions = 66 – 6!

Question 18: Let f : R → R be defined by

\(f(x)=\left\{\begin{matrix} 2x &;x>3 & \\ x^{2}&;1<x\leq 3 & \\ 3x& & ;x\leq 1 & \\ \end{matrix}\right.\)

Then f (–1) + f (2) + f (4) is

  1. a. 9
  2. b. 14
  3. c. 5
  4. d. 10

Solution:

  1. Answer: (a)

    ⇒ f (–1) + f (2)+ f (4)

    ⇒ 3 (–1) + (2)2 + 2 × 4

    ⇒ –3 + 4 + 8 = 9

Question 19: If sin-1 x + cos-1 y = 2π / 5, then cos-1 x + sin-1 y is

  1. a. 2π / 5
  2. b. 3π / 5
  3. c. 4π / 5
  4. d. 3π / 10

Solution:

  1. Answer: (b)

    ⇒ sin-1 x + cos-1 y = 2π / 5

    ⇒ (π / 2) - cos-1 x + (π / 2) - sin-1 y = 2π / 5

    ⇒ cos-1 x + sin-1 y = π - (2π / 5) = 3π / 5

Question 20: The value of the expression tan [(1 / 2) cos-1 (2 / √5)] is

  1. a. 2 − √5
  2. b. √5 − 2
  3. c. [√5 − 2] / 2
  4. d. 5 – √2

Solution:

  1. Answer: (b)

    tan [(1 / 2) cos-1 (2 / √5)]

    Let θ = (1 / 2) cos-1 (2 / √5) ∵ [θ ∈ (0, [π / 2])]

    ⇒ cos 2θ = 2 / √5 ⇒ (1 - tan2 θ) / (1 + tan2 θ) = 2 / √5

    ⇒ √5 - √5 tan2 θ = 2 + 2 tan2 θ

    ⇒ [√5 - 2] / [√5 + 2] = tan2 θ

    ⇒ tan2 θ = (√5 - 2)2

    ⇒ tan θ = ∓ (√5 - 2) ∵ [θ ∈ (0, [π / 2])]

    tan θ = √5 - 2

Question 21: IfKCET-2018 Maths Paper With Solutions Q21, then An = 2kA, Where k =

  1. a. 2n–1
  2. b. n +1
  3. c. n – 1
  4. d. 2 (n - 1)

Solution:

  1. Answer: (d)

    Solved KCET 2018 Maths Paper Q21

    Now check from option by putting n = 2 & 3

Question 22: IfKCET 2018 Maths Paper With Solutions Q22then the value of x and y respectively are

  1. a. –3, –1
  2. b. 1, 3
  3. c. 3, 1
  4. d. –1, 3

Solution:

  1. Answer: (d)

    KCET 2018 Maths Paper Q22

    x + y = 2 … (i)

    -x + y = 4 ... (ii)

    On solving equation (i) & (ii)

    We get

    x = –1

    y = 3

Question 23: IfKCET 2018 Maths Paper With Solutions Q23then AA’ =

  1. a. A
  2. b. Zero matrix
  3. c. A'
  4. d. I

Solution:

  1. Answer: (d)

    \(\\AA'=\begin{bmatrix} cos \alpha &sin \alpha \\ -sin \alpha& cos \alpha \end{bmatrix}\begin{bmatrix} cos \alpha &-sin \alpha \\ sin \alpha& cos \alpha \end{bmatrix}\\ =\begin{bmatrix} 1 &0 \\ 0&1 \end{bmatrix} =I\)

Question 24: If x, y, z ∈ R, then the value of the determinant KCET 2018 Maths Paper With Solutions Q24is

  1. a. 10
  2. b. 12
  3. c. 1
  4. d. 0

Solution:

  1. Answer: (d)

    KCET 2018 Maths Paper Q24

Question 25: The value of the determinantKCET 2018 Maths Paper With Solutions Q25is

  1. a. a3 + b3 + c3
  2. b. 3abc
  3. c. a3 + b3 + c3 –3abc
  4. d. a3 + b3 + c3 + 3abc

Solution:

  1. Answer: Bonus

Question 26: If (x1, y1), (x2, y2) and (x3, y3) are the vertices of a triangle whose area is ‘k’ square units, then KCET 2018 Maths Paper With Solutions Q26is

  1. a. 32 k2
  2. b. 16 k2
  3. c. 64 k2
  4. d. 48 k2

Solution:

  1. Answer: (c)

    KCET 2018 Maths Solved Paper

Question 27: Let A be a square matrix of order 3 × 3, then |5A| =

  1. a. 5|A|
  2. b. 125|A|
  3. c. 25|A|
  4. d. 15|A|

Solution:

  1. Answer: (b)

    |5A| = 53 |A| = 125 |A|

Question 28: If f (x) =

KCET 2018 Maths Paper With Solutions Q28

is continuous at x = 0, then the value of k is

  1. a. k = 1
  2. b. k = –1
  3. c. k = 0
  4. d. k = 2

Solution:

  1. Answer: (b)

    KCET 2018 Maths Paper Q28

    L.H.L = R.H.L

    k = –1

Question 29: If cos y = x cos (a + y) with cos a ≠ ± 1, then dy / dx is equal to

  1. a. sin a / cos2 (a + y)
  2. b. cos2 (a + y) / sin a
  3. c. cos a / sin2 (a + y)
  4. d. cos2 (a + y) / cos a

Solution:

  1. Answer: (b)

    cosy = x cos (a + y)

    ⇒ x = [cos y] / [cos (a + y)]

    ⇒ 1 = {[– cos (a + y) sin y + cos y sin (a + y)] (dy / dx)} / {cos2 (a + y)}

    ⇒ dy / dx = [cos2 (a + y)] / sin a

Question 30: If f (x) = |cos x - sin x|, then f ‘(π / 6) is equal to

  1. a. (-1 / 2) (1 + √3)
  2. b. (1 / 2) (1 + √3)
  3. c. (-1 / 2) (1 - √3)
  4. d. (1 / 2) (1 - √3)

Solution:

  1. Answer: (a)

    f (x) = | cosx – sinx |

    At x = π / 6,

    f (x) = cosx – sinx

    f’(x) = – sinx – cosx

    f ‘ (π / 6) = (-1 / 2) - (√3 / 2) = (-1 / 2) (1 + √3)

Question 31: If y =

\(y=\sqrt{x+\sqrt{x+\sqrt{x+....... \infty}}},\)
then dy / dx =

  1. a. 1 / [y2 - 1]
  2. b. 1 / [2y + 1]
  3. c. 2y / [y2 - 1]
  4. d. 1 / [2y – 1]

Solution:

  1. Answer: (d)

    y = √x + y

    y2 - y - x = 0

    2y (dy / dx) - (dy / dx) - 1 = 0

    dy / dx = 1 / (2y - 1)

Question 32: If f (x) = KCET 2018 Maths Paper With Solutions Q32is continuous at x = 1, then the value of k is

  1. a. e
  2. b. 1
  3. c. -1
  4. d. 0

Solution:

  1. Answer: (b)

    limx→1 [loge x / (x - 1)] [0 / 0]

    Using L-Hospital Rule

    limx→1 (1 / x) / 1 = 1

    LHL = RHL = f (1)

    1 = k

Question 33: Approximate change in volume V of a cube of side x metres caused by increasing the size by 3% is

  1. a. 0.09 x3 m3
  2. b. 0.03 x3 m3
  3. c. 0.06 x3 m3
  4. d. 0.04 x3 m3

Solution:

  1. Answer: (a)

    Δx = (3 / 100) × x = 0.03 x

    Δv = (dv / dx) × Δx

    Δv = 3x2 . 0.03x

    = 0.09 x3

Question 34: The maximum value of (1 / x)x is

  1. a. e
  2. b. ee
  3. c. e1/e
  4. d. [1 / e]1/e

Solution:

  1. Answer: (c)

    y = 1 / xx

    dy / dx = -x-x (1 + loge x) = 0

    = x = 1 / e (point of maxima)

    ymax = (e)1/e

Question 35: f (x) = xx has stationary point at

  1. a. x = e
  2. b. x = 1 / e
  3. c. x = 1
  4. d. x = √e

Solution:

  1. Answer: (b)

    f (x) = xx

    f ‘ (x) = xx (1 + logx) = 0

    x = 1 / e (stationary point)

Question 36: The maximum area of a rectangle inscribed in the circle (x + 1)2 + (y – 3)2 = 64 is

  1. a. 64 sq. units
  2. b. 72 sq. units
  3. c. 128 sq. units
  4. d. 8 sq. units

Solution:

  1. Answer: (c)

    KCET 2018 Maths Paper With Solutions Q36

    (x + 1)2 + (y - 3)2 = 64

    x2 + x2 = (16)2

    2x2 = 16 . 16

    x2 = 8.16

    x = 8√2

    Given rectangle is a square

    Area of square is = 8 √2 * 8 √2

    = 128 sq. units

Question 37: ∫(1 / [1 + ex]) dx is equal to

  1. a. loge [(ex + 1) / ex] + c
  2. b. loge [(ex - 1) / ex] + c
  3. c. loge [(ex) / (ex + 1)] + c
  4. d. loge [(ex) / (ex - 1)] + c

Solution:

  1. Answer: (c)

    ⇒ ∫(1 / [1 + ex]) dx

    ⇒ ∫(e-x / [1 + e-x]) dx

    Let 1 + e–x = t

    -e-x dx = dt

    ⇒ -∫dt / t

    ⇒ - lnt + c

    ⇒ ln |(1 / [1 + e-x])| + c

    ⇒ ln (ex / [1 + ex]) + c

Question 38: ∫1 / (√3 - 6x + 9x2) dx is equal to

  1. a. sin-1 ([3x + 1] / 2) + c
  2. b. sin-1 ([3x + 1] / 6) + c
  3. c. (1 / 3) sin-1 ([3x + 1] / 2) + c
  4. d. sin-1 ([2x + 1] / 3) + c

Solution:

  1. Answer: (c)

    ∫1 / (√3 - 6x + 9x2) dx

    = ∫1 / (√4 - (3x + 1)2

    = (1 / 3) sin-1 ([3x + 1] / 2) + c

Question 39: ∫esinx * ([sinx + 1] / secx) dx is equal to

  1. a. sin x. esin x + c
  2. b. cos x. esin x + c
  3. c. esin x + c
  4. d. esin x (sinx +1) + c

Solution:

  1. Answer: (a)

    ∫esinx * ([sinx + 1] / secx) dx

    Let sinx = t

    cosxdx = dt

    = ∫et (t + 1) dt

    = tet + c

    sin x. esin x + c

Question 40: ∫-22 | x cos πx| dx is equal to

  1. a. 8 / π
  2. b. 4 / π
  3. c. 2 / π
  4. d. 1 / π

Solution:

  1. Answer: (a)

    KCET 2018 Maths Paper With Solutions Q40

Question 41: ∫01 dx / (ex + e-x) is equal to

  1. a. (π / 4) - tan-1 e
  2. b. tan-1 e - (π / 4)
  3. c. tan-1 e + (π / 4)
  4. d. tan-1 e

Solution:

  1. Answer: (b)

    ∫01 dx / (ex + e-x)

    = ∫01 ex dx / [1 + e2x]

    Let ex = t

    ex dx = dt

    = ∫1e dt / (1 + t2 )

    = tan-1 (t)1e

    = tan-1 e - (π / 4)

Question 42: ∫01/2 dx / [(1 + x2) √1 - x2] is equal to

  1. a. (1 / √2) tan-1 (√(2 / 3))
  2. b. (2 / √2) tan-1 (3 / √2)
  3. c. (√2 / 2) tan-1 (3 / 2)
  4. d. (√2 / 2) tan-1 (√3 / 2)

Solution:

  1. Answer: (a)

    KCET 2018 Maths Paper With Solutions Q42

Question 43: The area of the region bounded by the curve y = cos x between x = 0 and x = π is

  1. a. 1 sq. unit
  2. b. 4 sq. units
  3. c. 2 sq. units
  4. d. 3 sq. units

Solution:

  1. Answer: (c)

    KCET 2018 Maths Paper With Solutions Q43

    A = ∫0π/2 cosx dx + |∫π/2π cos xdx|

    A = sinx|0π/2 + |sinx|π/2π

    A = 1 + |-1|

    = 2 sq. units

Question 44: The area bounded by the line y = x, x-axis and ordinates x = –1 and x = 2 is

  1. a. 3 / 2
  2. b. 5 / 2
  3. c. 2
  4. d. 3

Solution:

  1. Answer: (b)

    KCET 2018 Maths Paper With Solutions Q44

    A = |(1 / 2) (-1) (-1)| + (1 / 2) (2) (2)

    A = (1 / 2) + 2

    A = 5 / 2

Question 45: The degree and the order of the differential equation d2y / dx2 = ∛(1 + [dy / dx)]2 respectively are

  1. a. 2 and 3
  2. b. 3 and 2
  3. c. 2 and 2
  4. d. 3 and 3

Solution:

  1. Answer: (b)

    d2y / dx2 = ∛(1 + [dy / dx)]2

    d2y / dx2 = |(1 + [dy / dx)]2|⅓

    (d2y / dx2)3 = 1 + (dy / dx)2

    Order = 2 and degree = 3

Question 46: The solution of the differential equation x (dy / dx) – y = 3 represents a family of

  1. a. straight lines
  2. b. circles
  3. c. parabolas
  4. d. ellipses

Solution:

  1. Answer: (a)

    x (dy / dx) – y = 3

    (dy / dx) - (y / x) = 3 / x (Linear equation)

    IF = e-∫(1/x) dx = e-ln x = 1 / x

    y * IF = ∫(3 / x) * IF dx

    (y / x) = ∫(3 / x2) dx

    (y / x) = (-3 / x) + c

    y = -3 + xc (straight line)

Question 47: The integrating factor of (dy / dx) + y = (1 + y) / x is

  1. a. xex
  2. b. xe1/x
  3. c. ex / x
  4. d. x / ex

Solution:

  1. Answer: (c)

    (dy / dx) + y = (1 + y) / x

    (dy / dx) + y - (y / x) = (1 / x)

    (dy / dx) + y (1 - (1 / x)) = 1 / x

    IF = e∫(1 - (1 / x))dx = ex-ln x = ex * (1 / x)

Question 48: If

\(|\vec{a} \times \vec {b}|^{2}+|\vec{a} . \vec {b}|^{2}=144\)
and
\(|\vec{a}|=4\)
, then the value of
\(|\vec{b}|\)
is

  1. a. 1
  2. b. 2
  3. c. 3
  4. d. 4

Solution:

  1. Answer: (c)

    \(\\|\vec{a} \times \vec {b}|^{2}+|\vec{a} . \vec {b}|^{2}=144\\ |\vec{a}|^{2}+|\vec{b}|^{2}=144\\ |\vec{b}|^{2}=\frac{144}{16}=9\\ |\vec{b}|=3\)

Question 49: If a and b are mutually perpendicular unit vectors, then (3a + 2b) . (5a - 6b) =

  1. a. 5
  2. b. 3
  3. c. 6
  4. d. 12

Solution:

  1. Answer: (b)

    |a| = 1

    |b| = 1

    a . b = 0

    (3a + 2b) . (5a - 6b)

    = 15 - 18 (a . b) + 10 (a . b) - 12

    15 - 12 = 3

Question 50: If the vectors ai + j + k, i + bj + k+ and i + j + ck are coplanar (a ≠ b ≠ c ≠ 1) , then the value of abc – (a + b + c) =

  1. a. 2
  2. b. -2
  3. c. 0
  4. d. -1

Solution:

  1. Answer: (b)

    ∵ Vector one coplanar

    ∴ Δ = 0

    \(\begin{vmatrix} a &1 &1 \\ 1&b &1 \\ 1&1 &c \end{vmatrix}=0\\\)

    a (bc – 1) – (c – 1) + (1 – b) = 0

    abc – (a + b + c) = –2

Question 51: If a = i + λj + 2k, b = μi + j - k are orthogonal and |a| = |b| then (λ, μ) =

  1. a. (1 / 4 , 7 / 4)
  2. b. (7 / 4, 1 / 4)
  3. c. (1 / 4, 9 / 4)
  4. d. (-1 / 4, 9 / 4)

Solution:

  1. Answer: (a)

    a . b = 0

    μ + λ = 2 ---- (1)

    |a| = |b|

    √1 + λ2 + 4 = √μ2 + 1 + 1

    λ2 + 3 = μ2 ---- (2)

    Put equation (1) in equation (2),

    λ2 + 3 = (2 - λ)2

    3 = 4 - 4λ

    λ = 1 / 4

    μ = 2 - (1 / 4) = 7 / 4 {using equation (1)}

Question 52: The image of the point (1, 6, 3) in the line (x / 1) = (y - 1) / 2 = (z - 2) / 3 is

  1. a. (1, 0, 7)
  2. b. (7, 0, 1)
  3. c. (2, 7, 0)
  4. d. (–1, –6, –3)

Solution:

  1. Answer: (a)

    PQ d.r is = ((a – 1), (b – 6), (c – 3))

    (x / 1) = (y - 1) / 2 = (z - 2) / 3 = t

    KCET 2018 Maths Paper With Solutions Q52

    x = t, y = 2t + 1, z = 3t + 2 …(1)

    O ≡ (t, 2t + 1, 3t + 2)

    ∵ OP ⟂r dr of line

    (1 – t) . 1 + 2 (6 – 2t – 1) + 3 (3 – 3t – 2) = 0

    1 – t + 10 – 4t + 3 - 9t = 0

    14t = 14

    t = 1

    O = (1, 3, 5)

    Q = [(2 - 1), (6 - 6), (10 - 3)]

    Q = (1, 0, 7)

Question 53: The angle between the lines 2x = 3y = –z and 6x = –y = –4z is

  1. a. 0º
  2. b. 45º
  3. c. 90º
  4. d. 30º

Solution:

  1. Answer: (c)

    (x / 3) = (y / 2) = (z / -6) ---- (1)

    (x / -4) = (y / 24) = (z / 6) ---- (2)

    cos θ = [-12 + 48 - 36] / [√9 + 4 + 36] [√16 + 242 + 36]

    cos θ = 0

    θ = π / 2

Question 54: The value of k such that the line (x - 4) / 1 = (y - 2) / 1 = (z - k) / 2 lies on the plane 2x – 4y + z = 7 is

  1. a. –7
  2. b. 4
  3. c. –4
  4. d. 7

Solution:

  1. Answer: (d)

    Point (4,2,k) of the line will be on the plane.

    So points will satisfy the plane.

    2 (4) – 4 (2) + k = 7

    k = 7

Question 55: The locus represented by xy + yz = 0 is

  1. a. a pair of perpendicular lines
  2. b. a pair of parallel lines
  3. c. a pair of parallel planes
  4. d. a pair of perpendicular planes

Solution:

  1. Answer: (d)

    y (x + z) = 0

    y = 0 or x + z = 0

    p1: y = 0 ⇒ n1 = j

    p2 : x + z = 0 ⇒ n2 = i + k

    n1 . n2 = j (i + k) = 0

    n1 ⟂r n2

    A pair of perpendicular planes.

Question 56: The feasible region of an LPP is shown in the figure. If z = 3x + 9y, then the minimum value of z occurs at

KCET 2018 Maths Paper With Solutions Q56

  1. a. (5, 5)
  2. b. (0, 10)
  3. c. (0, 20)
  4. d. (15, 15)

Solution:

  1. Answer: (a)

    Z = 3x + 9y

    Z (0, 10) = 90

    Z (5, 5) = 60

    Z (0, 20) = 180

    Z (15, 15) = 180

    Zmin = 60 at (5, 5)

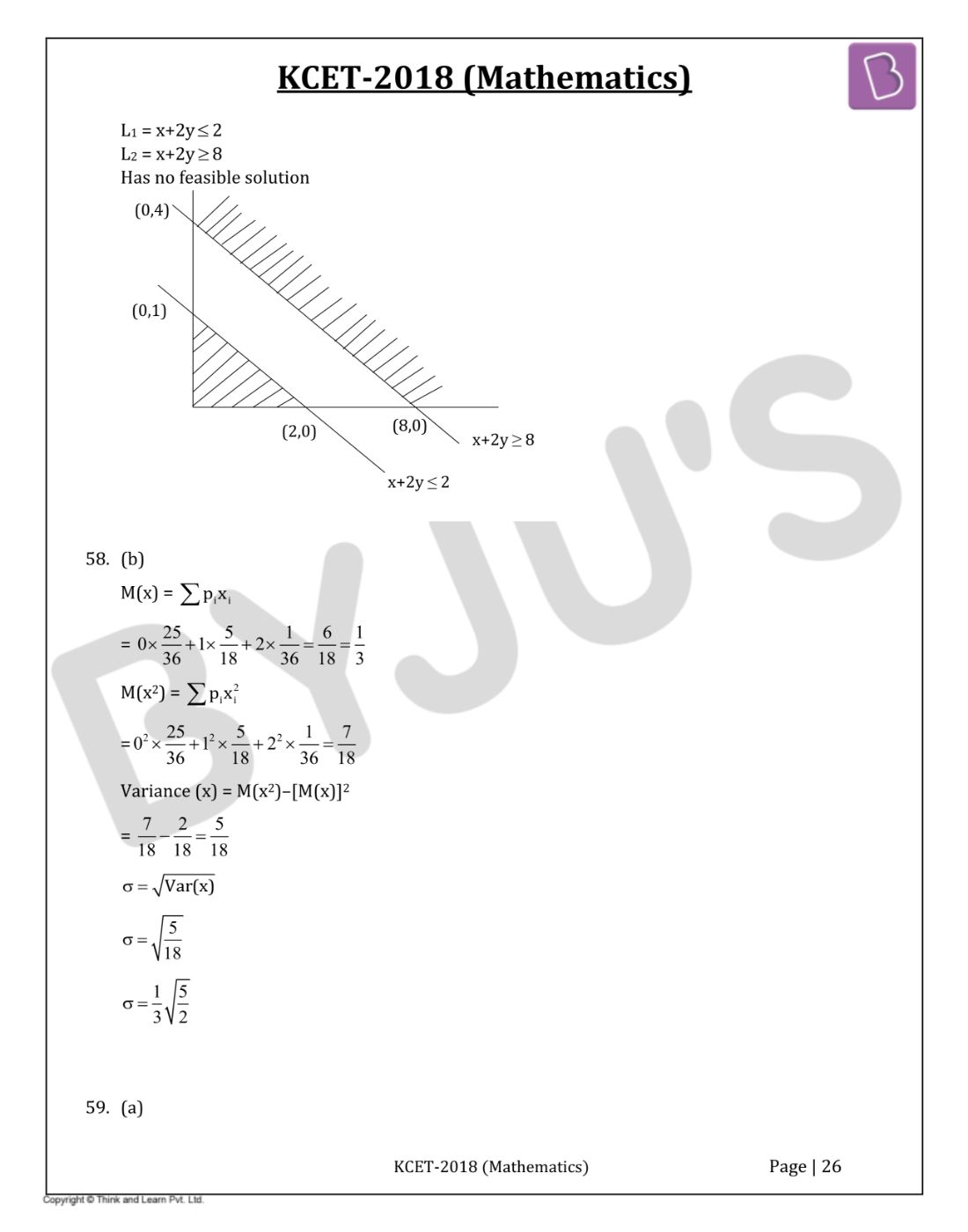
Question 57: For the LPP; maximize z = x + 4y subject to the constraints x + 2y ≤ 2, x + 2y ≥ 8, x, y ≥ 0

  1. a. zmax = 4
  2. b. zmax = 18
  3. c. zmax = 16
  4. d. Has no feasible solution

Solution:

  1. Answer: (d)

    L1 = x + 2y ≤ 2

    L2 = x+2y ≥ 8

    Has no feasible solution

Question 58: For the probability distribution given by

X = xi

0

1

2

Pi

25 / 36

5 / 18

1 / 36

The standard deviation (σ) is

  1. a. √(1 / 3)
  2. b. (1 / 3) √5 / 2
  3. c. √(5 / 36)
  4. d. None of the above

Solution:

  1. Answer: (b)

    M (x) = ∑ pixi

    = 0 * (25 / 36) + 12 * (5 / 18) + 22 * (1 / 36) = 6 / 18 = 1 / 3

    M (x2) = ∑ pixi2

    = 02 * (25 / 36) + 12 * (5 / 18) + 22 * (1 / 36) = 7 / 18

    Variance = M (x2) - [M(x)]2

    = (7 / 18) - (2 / 18) = 5 / 18

    σ = √(var (x))

    = √(5 / 18)

    = (1 / 3) √5 / 2

Question 59: A bag contains 17 tickets numbered from 1 to 17. A ticket is drawn at random, then another ticket is drawn without replacing the first one. The probability that both the tickets may show even numbers is

  1. a. 7 / 34
  2. b. 8 / 17
  3. c. 7 / 16
  4. d. 7 / 17

Solution:

  1. Answer: (a)

    In bag → 1, 2, 3, ………………..17 → tickets

    Even no → 2, 4, 6, 8, 10, 14, 16 → 8 even numbers

    The probability of getting even no. at the first time = 8 / 17

    The probability of getting even no. at second time = 7 / 16

    The probability that both the ticket may show Even numbers = (8 / 17) * (7 / 16) = 7 / 34

Question 60: A flashlight has 10 batteries out of which 4 are dead. If 3 batteries are selected without replacement and tested, then the probability that all 3 are dead is

  1. a. 1 / 30
  2. b. 2 / 8
  3. c. 1 / 15
  4. d. 1 / 10

Solution:

  1. Answer: (a)

    Total batteries =10

    Dead batteries = 4

    The probability of battery to be dead = 4 / 10

    The probability that all 3 batteries are dead

    = (4 / 10) * [3C1 / 9C1] * [2C1 / 8C1]

    = (4 / 10) * (3 / 9) * (2 / 8)

    = 1 / 30

Video Lessons - KCET 2018 - Maths











KCET 2018 Maths Question Paper with Solutions

KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions
KCET 2018 Maths Question Paper with Solutions