Coordinate Geometry Class 9 Notes - Chapter 3

CBSE Class 9 Maths Coordinate Geometry Notes:-Download PDF Here

Coordinate geometry is significant because it provides a link between geometry and algebra through line graphs and curves. Coordinate geometry is useful in mathematics because it allows us to locate points on any plane. It also has applications in trigonometry, calculus, and other disciplines. Get the complete concept of coordinate geometry, such as the Cartesian system, coordinate points, how to plot the points in the coordinate axes, quadrants with signs, and so on. Go through the below article to learn coordinate geometry for Class 9.

To know more about coordinate geometry, click here.

Cartesian System

The Cartesian system is a system for describing the position of a point in a plane. A point is located by referring to two perpendicular lines in a Cartesian system. The X-axis is the horizontal line XX’, and the Y-axis is the vertical line YY’.

To know more about the coordinate system, click here.

Origin

The origin, indicated by the letter ‘O,’ is the place where the horizontal and vertical lines intersect. Here, positive directions are OX and OY, while negative directions are OX’ and OY’.

Coordinate Axes and Quadrants

The plane is divided into four sections by the X and Y axes. The quadrants (one-fourth section) are numbered I, II, III, and IV in anti-clockwise order from OX. The Cartesian plane, also known as the coordinate plane or the XY plane, comprises these axes and quadrants. These axes are also known as coordinate axes.

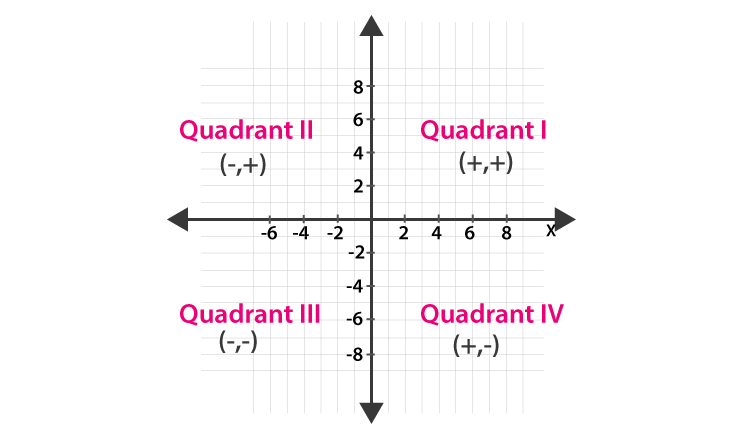
Points in Different Quadrants

Signs of coordinates of points in different quadrants:

I Quadrant: ‘+’ x – coordinate and ‘+’ y – coordinate. Eg. (2, 3)

II Quadrant: ‘-’ x – coordinate and ‘+’ y – coordinate. Eg. (-1, 4)

III Quadrant: ‘-’ x – coordinate and ‘-’ y – coordinate. Eg. (-3, -5)

IV Quadrant: ‘+’ x – coordinate and ‘-’ y – coordinate. Eg. (6, -1)

To know more about Quadrants, visit here.

Plotting on a Graph

Using the coordinate axes, we can describe any point in the plane using an ordered pair of numbers. Point A is represented by an ordered pair $(x,y)$ where $x$ is the abscissa and $y$ is the ordinate of the point.

Position of a point in a plane

To know more about the Cartesian plane, visit here.

Plotting a Point in the Plane if Its Coordinates Are Given

The coordinate points will define the location in the Cartesian plane. The distance of a point from the y-axis is known as the x-coordinate or abscissa, and the distance of the point from the x-axis is known as the y-coordinate, or ordinate.
For example, Point (3, 2) is 3 units away from the positive y-axis and 2 units away from the positive x-axis. Therefore, a point (3, 2) can be plotted below. Similarly, (-2, 3), (-1, -2) and (2, -3) are plotted.

Plotting a point in the plane

Solved Example on Class 9 Maths Chapter 3 Coordinate Geometry

Example:

Each of the coordinates (-2, 4),(3, -1), (-1, 0),(1, 2), and (-3, -5) lies in which quadrant or on which axis? Locate them on the Cartesian plane to verify your solution.

Solution:

Negative abscissa and positive ordinate characterize the point (-2, 4).

(-2,4) is located in the second quadrant.

Positive abscissa and negative ordinate characterize the position (3, -1).

(3, -1) is located in the fourth quadrant.

Negative abscissa and zero ordinate characterize the point (-1, 0).

∴ On the negative x-axis is the point (-1, 0).

The abscissa and ordinate are both positive at points (1, 2).

∴ The first quadrant contains points (1,2).

Both the abscissa and ordinate are negative at the location (-3, -5).

∴ The 3rd quadrant contains the point (-3, -5).

These points are represented in the Cartesian plane as A(-2, 4), B(3, -1), C(-l, 0), D(l, 2), and E (-3, -5), as shown in the diagram.

Video lesson on Coordinate Geometry toughest problems